Metode de calcul ale Electrostaticii Prezentare
succinta
Prin metodele electrostaticii se va intelege metodele de
determinare a campurilor si potentialelor electrostatice in diferite
medii sau corpuri.
Printre metodele mai importante se
pot enumera: 1. metoda elementara; 2. metoda imaginilor; 3. metoda
ecuatiei Laplace; 4. metoda diferentelor finite.
In
continuare vor fi prezentate, pe scurt, unele dintre aceste metode si
anume: 1. metoda elementara, 3. metoda ecuatiei Laplace si 4.
metoda diferentelor finite.
Metoda
elementara
Aceasta metoda consta
in aplicarea legilor si teoremelor specifice regimului electrostatic sub
forma integrala. Este usor aplicabila in cazul in care corpurile,
respectiv campul electric, prezinta proprietati de simetrie,
care permit stabilirea directa a formei liniilor de camp.
Exemplu
Se va calcula campul electric
si potentialul unui fir rectiliniu infinit, de forma
cilindrica, incarcat uniform cu densitatea de sarcina  (fig. 3.6.1).
(fig. 3.6.1).
Se observa ca in acest caz
campul este radial si identic in toate punctele pe directia unei raze
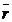 , aflate la egala distanta de axul
conductorului. Se va alege o suprafata
, aflate la egala distanta de axul
conductorului. Se va alege o suprafata  de forma unui cilindru
care circumscrie o portiune din conductor, coaxial cu aceasta, si se
va aplica teorema lui Gauss acestei
suprafete:
de forma unui cilindru
care circumscrie o portiune din conductor, coaxial cu aceasta, si se
va aplica teorema lui Gauss acestei
suprafete:
Dar:
|
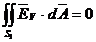 si si 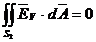
|
|
vectorii 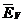 si
si  in acest fiind
perpendiculari intre ei.
in acest fiind
perpendiculari intre ei.
Ramane din
integrala doar termenul referitor la suprafata laterala, astfel
ca:
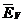 si
si 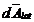 fiind omoparaleli.
fiind omoparaleli.
Integrand relatia
(3.6.2) se obtine:
|

|
|
Fig. 3.6.1 Fir rectiliniu
infinit de forma cilindrica, incarcat uniform
|
|
Pe de alta parte,
conform aceleiasi teoreme se poate scrie:
Prin egalarea celor
doua expresii (3.6.3) si (3.6.4)
se obtine expresia campului
electric  sub forma:
sub forma:
Cum 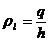 , rezulta
, rezulta  si, inlocuind in
(3.6.5), rezulta:
si, inlocuind in
(3.6.5), rezulta:
sau, vectorial:
Relatia
(3.6.7) exprima intensitatea campului electric 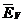 intr-un punct oarecare
P, la distanta
intr-un punct oarecare
P, la distanta 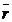 de axul conductorului,
considerand raza acestuia comparabila cu aceasta distanta (
de axul conductorului,
considerand raza acestuia comparabila cu aceasta distanta (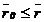 ).
).
Potentialul
electric intr-un punct oarecare P,
situat in exteriorul conductorului, este
dat de relatia:
presupunand punctul 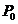 chiar si pe
suprafata conductorului infinit.
chiar si pe
suprafata conductorului infinit.
Rezulta:
relatie care se mai
poate scrie sub forma:
Metoda
ecuatiei Laplace
Pentru a obtine ecuatia
lui Laplace intr-un dielectric omogen ( ), aflat in camp electric, se va inlocui expresia
), aflat in camp electric, se va inlocui expresia 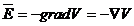 (forma locala a
teoremei potentialului electrostatic) in expresia
(forma locala a
teoremei potentialului electrostatic) in expresia  (forma locala a
legii fluxului electric), in conditiile in care in dielectric nu
exista distributie de sarcina electrica libera (
(forma locala a
legii fluxului electric), in conditiile in care in dielectric nu
exista distributie de sarcina electrica libera ( ):
):
Dezvoltand relatia
(3.6.11), se obtine ecuatia lui Laplace:
ce caracterizeaza in
orice punct P un dielectric lipsit de sarcini si strabatut de
liniile de camp electrostatic (fig. 3.6.2)
|

|
|
Fig. 3.6.2 Dielectric omogen ( ), aflat in camp electric ), aflat in camp electric
|
Exemplu
Se va determina expresia potentialului electrostatic
in orice punct din dielectricul unui condensator plan (fig. 3.6.3).
|

|
|
Fig.3.6.3 Condensator electric
plan
|
|
In
acest scop, se poate utiliza metoda ecuatiei Laplace, deoarece in
dielectric  si dielectricul
este omogen (
si dielectricul
este omogen (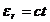 ).
).
Cum
campul electric se dezvolta numai dupa directia Ox, ecuatia
Laplace se simplifica in acest caz, ramanand:
Integrand de doua ori
succesiv relatia (3.6.13), se obtine:
constantele  si
si 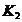 fiind determinate in
urmatoarele conditii:
fiind determinate in
urmatoarele conditii:
a. se alege originea
potentialelor pe prima armatura, astfel ca pentru x=0; rezulta V(x)=V(0)=0 si, de aici, 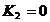 ;
;
b. se considera pe
armatura din stanga sarcina +q
si se aplica legea fluxului electric unei suprafete  inchisa care
cuprinde aceasta armatura:
inchisa care
cuprinde aceasta armatura:
Cum 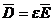 , pentru dielectrici liniari,
, pentru dielectrici liniari,
 devine:
devine:
Se inlocuieste 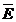 din expresia:
din expresia:
in cea a fluxului
electric, obtinand:
Deoarece 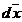 si
si 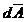 sunt omoparaleli, se
mai poate scrie:
sunt omoparaleli, se
mai poate scrie:
Suprafata
armaturii condensatorului fiind A,
rezulta:
Cum insa, din rel. (3.6.14)
:
Inlocuind derivata in
(3.6.19), se obtine:
De unde:
|
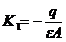 . .
|
|
Inlocuind pe  in expresia
potentialului (3.6.14) ,rezulta, in final:
in expresia
potentialului (3.6.14) ,rezulta, in final:
Pentru x=o,
V(0)=0, iar pentru x=d:
Verificarea se poate face
prin calculul capacitatii electrice a condensatorului plan, utilizand
expresia potentialului (3.6.22):
Metoda
diferentelor finite
O metoda aproximativa,
utilizata in cazul corpurilor cu forme diferite, este metoda diferentelor finite - metoda cu eroare
controlabila care foloseste in locul ecuatiilor cu derivate
partiale ale potentialului ecuatii cu diferente finite. Se
presupune, in acest caz, ca potentialul pe frontiera corpului
analizat este dat (cunoscut).
Fie un domeniu bidimensional 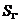 , caracterizat printr-un camp laplaceian (fara
distributie de sarcina electrica, continand numai linii de camp). Se pune problema
determinarii repartitiei potentialului electric in acest domeniu
(fig. 3.6.4). Pentru aceasta se va imparti domeniul in mici
patrate de latura h si
se vor nota nodurile retelei astfel obtinute cu
, caracterizat printr-un camp laplaceian (fara
distributie de sarcina electrica, continand numai linii de camp). Se pune problema
determinarii repartitiei potentialului electric in acest domeniu
(fig. 3.6.4). Pentru aceasta se va imparti domeniul in mici
patrate de latura h si
se vor nota nodurile retelei astfel obtinute cu  (unde k = 1n).
(unde k = 1n).
Fiecare
punct  are coordonatele (
are coordonatele ( ) si potentialul
) si potentialul  .
.
|

|
|
Fig. 3.6.4 Domeniu
bidimensional 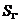 de camp
electrostatic de camp
electrostatic
|
Se dezvolta in serie
Taylor potentialele 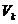 din jurul
fiecarui nod
din jurul
fiecarui nod  ,
,
unde i = 1.4, dupa care se
scriu potentialele punctelor in functie de potentialul  :
:
Se aduna aceste
ecuatii si se obtine:
Fiind
vorba de un camp Laplaceian, potentialul in fiecare punct al domeniului 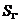 va satisface
ecuatia lui Laplace, care in acest caz are forma:
va satisface
ecuatia lui Laplace, care in acest caz are forma:
Problema
care se pune deci este de a gasi solutia acestei ecuatii care ia
pe frontiera 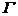 a domeniului
a domeniului 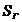 anumite valori
(conditiile de frontiera).
anumite valori
(conditiile de frontiera).
Neglijand
in rel. (3.6.26) termenii in  si tinand
seama de ecuatia (3.6.27), se obtine ecuatia lui Laplace in
diferente finite, bidimensionale, de forma:
si tinand
seama de ecuatia (3.6.27), se obtine ecuatia lui Laplace in
diferente finite, bidimensionale, de forma:
care se poate explicita in
raport cu  :
:
Concluzie:
Potentialul unui nod al retelei este egal cu media aritmetica a
potentialelor nodurilor vecine.
Scriind astfel de relatii ( ) pentru toate nodurile si tinand seama de valorile
pe frontiera impuse potentialului (considerate aceleasi si in
nodurile din vecinatatea frontierei), se obtine un sistem de n ecuatii cu n necunoscute. Pentru rezolvarea sistemului se poate utiliza metoda
lui Cramer sau o metoda de numerica, folosind calculatorul
electronic.
) pentru toate nodurile si tinand seama de valorile
pe frontiera impuse potentialului (considerate aceleasi si in
nodurile din vecinatatea frontierei), se obtine un sistem de n ecuatii cu n necunoscute. Pentru rezolvarea sistemului se poate utiliza metoda
lui Cramer sau o metoda de numerica, folosind calculatorul
electronic.









