Metode de calcul pentru optimizarea cu restrictii
In cazul existentei unor restrictii se folosesc atat metode de
calcul bazate pe transformari ale problemelor cu restrictii in
probleme fara restrictii, cat si metode specifice; in cadrul
ambelor categorii de metode, o importanta deosebita o au conditiile
Kuhn-Tucker.
Folosirea multiplicatorilor Lagrange pentru
rezolvarea problemelor cu restrictii de tip egalitate este ilustrata in
paragraful 2.1, conditiile Kuhn-Tucker sunt enuntate in paragraful 2.2,
utilizarea functiilor de penalizare pentru rezolvarea problemelor cu
restrictii de tip egalitate si inegalitate este prezentata in
paragraful 2.3, iar cele mai utilizate metode specifice de rezolvare a
problemelor cu restrictii sunt ilustrate in paragraful 2.4.
1. Folosirea multiplicatorilor Lagrange pentru rezolvarea problemelor de
optim cu
restrictii de tip egalitate
In cazul cautarii extremului (de
exemplu, a maximului) unei functii criteriu de n variabile
 (2.1)
(2.1)
cu m restrictii de tip egalitate
 (2.2)
(2.2)
i 1, 2, , m (cu m < n), se
demonstreaza [Bri05] ca punctul 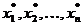 care maximizeaza functia criteriu (2.1),
cu respectarea restrictiilor (2.2), poate fi obtinut prin optimizarea
(maximizarea) fara restrictii a functiei
care maximizeaza functia criteriu (2.1),
cu respectarea restrictiilor (2.2), poate fi obtinut prin optimizarea
(maximizarea) fara restrictii a functiei
L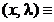 L
L
Functia L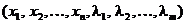 este
denumita functie Lagrange (sau lagrangean), iar scalarii l l lm sunt numiti multiplicatorii
Lagrange [Bri05].
este
denumita functie Lagrange (sau lagrangean), iar scalarii l l lm sunt numiti multiplicatorii
Lagrange [Bri05].
Extremul (in exemplul considerat in continuare,
extremul este un maxim) functiei Lagrange se obtine prin intermediul
conditiilor (1.12) aplicate acestei functii, respectiv
 L
L
 L
L (2.4)
(2.4)
 L
L
Conditiile (1.12) raman valabile, intrucat se cauta extremul
fara restrictii al functiei L
Metoda
multiplicatorilor Lagrange rezolva deci probleme de optim cu
restrictii de tip egalitate prin transformarea lor in probleme de optim
fara restrictii
Pentru ilustrare, se considera [Cal79] maximizarea
functiei criteriu din (1.29)
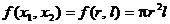 , (2.5)
, (2.5)
- reprezentand
volumul unui rezervor cilindric - in conditiile restrictiei care rezulta
din (1.30) respectiv
 (2.6)
(2.6)
Aplicand (2.3) se obtine
L 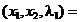 L
L 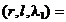

 (2.7)
(2.7)
Pentru gasirea valorilor optime ropt si lopt se anuleaza derivatele
partiale ale functiei L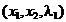 in raport
cu x1 si x2, conform cu (2.4), rezultand
din (2.7):
in raport
cu x1 si x2, conform cu (2.4), rezultand
din (2.7):
 L
L
 L
L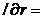
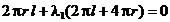 (2.8)
(2.8)
 L
L
 L
L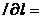
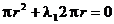 (2.9)
(2.9)
Din (2.9) se obtine
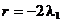
iar din (2.8) rezulta:  , respectiv
, respectiv
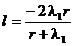 (2.11)
(2.11)
Inlocuind (2.10) in (2.11) se obtine
 , (2.12)
, (2.12)
din (3.10) si
(3.12) rezultand
 , (2.13)
, (2.13)
Inlocuind (2.10) si (2.12) in restrictia (2.6) se obtine
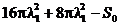 ,
,
de unde rezulta
valoarea multiplicatorului Lagrange:
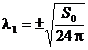 (2.14)
(2.14)
Intrucat raza r si inaltimea
l trebuie sa satisfaca si
conditiile de pozitivitate din (2.10) si (2.12) rezulta ca in
(2.14) trebuie adoptata valoarea
 (2.15)
(2.15)
care - prin inlocuire
in (2.10) si (2.12) - asigura obtinerea valorilor optime
pozitive:
 ,
,  (2.16)
(2.16)
Metoda multiplicatorilor Lagrange poate fi utilizata si in cazul
restrictiilor de tip inegalitate, cu conditia ca acestea sa fie in
prealabil aduse la forma unor restrictii de tip egalitate; o asemenea
schimbare a formei restrictiilor poate fi obtinuta prin
intermediul unor variabile auxiliare.
Astfel, presupunand ca se urmareste maximizarea functiei
criteriu  cu restrictiile inegalitate de forma
cu restrictiile inegalitate de forma
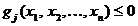 j
= 1, 2, , p, (2.17)
j
= 1, 2, , p, (2.17)
aceste restrictii
pot fi transformate in restrictii egalitate prin introducerea unor
variabile auxiliare kj (j = 1, 2, , p), scriind p egalitati
de forma
 , (2.18)
, (2.18)
acestea reprezentand
restrictiile egalitate corespunzatoare restrictiilor inegalitate
din (2.17).
Din (2.17) si (2.18) se constata ca satisfacerea egalitatilor
(2.18) asigura si satisfacerea
inegalitatilor (2.17), intrucat 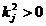 daca
daca  .
.
Restrictiile egalitate (2.18) permit folosirea metodei
multiplicatorilor Lagrange pentru gasirea optimului functiei
criteriu.
2. Conditiile Kuhn-Tucker
Conditiile Kuhn-Tucker au o importanta deosebita in
cazul optimizarii cu restrictii de tip inegalitate. In prezenta
acestui tip de restrictii, relatia (1.12) nu mai este valabila,
dupa cum va rezulta si din exemplul care urmeaza (Fig. 3.1);
presupunand ca extremul este un minim, conditiile Kuhn-Tucker afirma
ca prin deplasare din punctul de optim  in orice directie
admisibila - respectiv in orice directie care nu determina incalcarea
vreunei restrictii - functia criteriu nu poate descreste.
in orice directie
admisibila - respectiv in orice directie care nu determina incalcarea
vreunei restrictii - functia criteriu nu poate descreste.
Evident, daca din  ar exista vreo directie
admisibila in care functia criteriu ar descreste, atunci
ar exista vreo directie
admisibila in care functia criteriu ar descreste, atunci  nu ar mai fi punctul
de minim.
nu ar mai fi punctul
de minim.
Acest paragraf nu isi propune sa prezinte demonstratia conditiilor
Kuhn-Tucker, ci numai sa ilustreze formularea lor prin intermediul exemplului
din [Cal79]; demonstratia poate fi gasita in [Las75],
[Bri05]
Presupunand ca se cere minimizarea functiei criteriu
 (2.19)
(2.19)
cu restrictiile
 (2.20)
(2.20)
si
 , (2.21)
, (2.21)
in Fig. 3.1 sunt
reprezentate in planul  curbele circulare de nivel precum si parabola P si dreapta D, corespunzatoare cazurilor limita ale
restrictiilor (2.20) si (2.21), respectiv corespunzatoare egalitatilor
curbele circulare de nivel precum si parabola P si dreapta D, corespunzatoare cazurilor limita ale
restrictiilor (2.20) si (2.21), respectiv corespunzatoare egalitatilor
 (2.22)
(2.22)
 , (2.23)
, (2.23)
care pot
fi puse sub forma
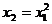 (2.24)
(2.24)
 (2.25)
(2.25)
Dreapta D este determinata
de intersectia dintre planul  si planul prin care este
reprezentata in
si planul prin care este
reprezentata in  functia
functia
 (2.26)
(2.26)
iar parabola P este determinata de intersectia
dintre planul  si suprafata prin care
este reprezentata in
si suprafata prin care
este reprezentata in  functia
functia
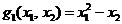 (2.27)
(2.27)
Din (2.20) rezulta ca punctele care corespund conditiei
 (2.28)
(2.28)
constituie
domeniul admisibil in planul  , iar punctele
care corespund conditiei
, iar punctele
care corespund conditiei
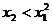 (2.29)
(2.29)
corespund
domeniului interzis, intrucat incalca restrictia (2.20); domeniul
interzis este hasurat in Fig. 3.1. In mod
analog este hasurat domeniul 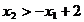 ,
reprezentand domeniul interzis de restrictia (2.21).
,
reprezentand domeniul interzis de restrictia (2.21).
Rezulta ca din punct de vedere al respectarii ambelor
restrictii (2.20) si (2.21), domeniul admisibil este cel precizat in Fig.
3.1, incluzand si portiunile aferente din parabola P si dreapta D.
Intrucat valorile functiei criteriu  scad dinspre curba circulara, de nivel C1 spre curba C6, pentru a atinge valoarea
zero in punctul de minim M, cu
coordonatele x1 = 2, x2 = 1, se constata,
ca - in conditiile respectarii restrictiilor - punctul care
asigura cea mai mica valoare a functiei criteriu este punctul E, cu coordonatele x1 = 1, x2
= 1 (de la intersecta dreptei D
cu parabola P), acesta reprezentand
solutia
scad dinspre curba circulara, de nivel C1 spre curba C6, pentru a atinge valoarea
zero in punctul de minim M, cu
coordonatele x1 = 2, x2 = 1, se constata,
ca - in conditiile respectarii restrictiilor - punctul care
asigura cea mai mica valoare a functiei criteriu este punctul E, cu coordonatele x1 = 1, x2
= 1 (de la intersecta dreptei D
cu parabola P), acesta reprezentand
solutia  a problemei de optimizare cu restrictii.
a problemei de optimizare cu restrictii.
Dupa cum s-a mentionat si la inceputul acestui paragraf, se
constata ca in E nu are loc
relatia (1.12), care este valabila numai in punctul M, insa acesta nu apartine
domeniului admisibil.
In Fig. 3.1 sunt reprezentati vectorul gradientului  in punctul E (vector perpendicular pe tangenta la
curba circulara, de nivel C2,
deci avand directia razei cercului si sensul spre curbele de nivel cu
valori descrescatoare C1)
si vectorul -
in punctul E (vector perpendicular pe tangenta la
curba circulara, de nivel C2,
deci avand directia razei cercului si sensul spre curbele de nivel cu
valori descrescatoare C1)
si vectorul - , de sens opus, prelungirea acestui vector trecand prin
punctul M.
, de sens opus, prelungirea acestui vector trecand prin
punctul M.
Observatie. Din orice punct considerat (facand
abstractie de existenta restrictiilor) prelungirea oricarui
vector - trece prin minimul fara restrictii M, datorita faptului ca
curbele de nivel sunt circulare. Acest considerent conduce la concluzia ca
in cazul unor curbe de nivel circulare, metoda celei mai mari pante, cu
alegerea directiei initiale p
= -
trece prin minimul fara restrictii M, datorita faptului ca
curbele de nivel sunt circulare. Acest considerent conduce la concluzia ca
in cazul unor curbe de nivel circulare, metoda celei mai mari pante, cu
alegerea directiei initiale p
= -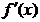 din (1.26), conduce intr-un singur pas pana la minimul
fara restrictii, intrucat prin deplasarea pe aceasta directie
se ajunge in minim si nu trebuie cautata o alta directie.
Pe aceasta baza a fost elaborata metoda gradientului conjugat
scalat [Cal79], care este indicata
atunci cand prin operatii de modificare a scalei - de scalare - curbele de
nivel de anumite forme (de exemplu, elipse) pot fi transformate in cercuri.
din (1.26), conduce intr-un singur pas pana la minimul
fara restrictii, intrucat prin deplasarea pe aceasta directie
se ajunge in minim si nu trebuie cautata o alta directie.
Pe aceasta baza a fost elaborata metoda gradientului conjugat
scalat [Cal79], care este indicata
atunci cand prin operatii de modificare a scalei - de scalare - curbele de
nivel de anumite forme (de exemplu, elipse) pot fi transformate in cercuri.
Tot in Fig. 3.1 sunt reprezentati si vectorii gradient ai restrictiilor
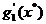 si
si  , ultimul fiind perpendicular in E pe dreapta D si avand
sensul spre zona admisibila (deci sensul cresterii valorilor functiei
, ultimul fiind perpendicular in E pe dreapta D si avand
sensul spre zona admisibila (deci sensul cresterii valorilor functiei
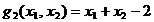 ), iar primul fiind perpendicular in E pe tangenta T la
parabola P (ecuatia tangentei T in
E la curba
), iar primul fiind perpendicular in E pe tangenta T la
parabola P (ecuatia tangentei T in
E la curba 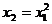 fiind
fiind 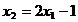 ) avand sensul spre zona admisibila, respectiv sensul
creserii functiei
) avand sensul spre zona admisibila, respectiv sensul
creserii functiei 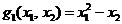 .
.
Esenta conditiilor Kuhn-Tucker consta in exprimarea faptului
ca vectorul - trebuie sa se gaseasca intre vectorii
trebuie sa se gaseasca intre vectorii 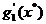 si
si  - folosind o formulare mai riguroasa: trebuie sa se
gaseasca in conul convex generat de vectorii
- folosind o formulare mai riguroasa: trebuie sa se
gaseasca in conul convex generat de vectorii 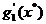 si
si  - respectiv trebuie sa
reprezinte o combinatie liniara a acestor vectori, de forma
- respectiv trebuie sa
reprezinte o combinatie liniara a acestor vectori, de forma
 (2.30)
(2.30)
unde 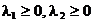 reprezinta
multiplicatori Lagrange ai restrictiilor.
reprezinta
multiplicatori Lagrange ai restrictiilor.
Intr-adevar, din punct de vedere al restrictiei g1(x), directiile admisibile p
sunt cele care fac unghiuri mai mari de 90° cu vectorul 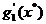 , iar din punct de vedere al restrictiilor g2(x), directiile admisibile p
sunt cele care fac unghiuri mai mari de 90° cu vectorul
, iar din punct de vedere al restrictiilor g2(x), directiile admisibile p
sunt cele care fac unghiuri mai mari de 90° cu vectorul  , intrucat acesti vectori sunt perpendiculari pe
tangenta T si dreapta D si deci orice directie care
face unghiuri pana la 90° cu vectorii
, intrucat acesti vectori sunt perpendiculari pe
tangenta T si dreapta D si deci orice directie care
face unghiuri pana la 90° cu vectorii 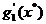 sau
sau  conduce la deplasari
spre zona interzisa, neadmisibila; ca urmare, numai directiile p care fac unghiuri mai mari de 90° cu
ambii vectori
conduce la deplasari
spre zona interzisa, neadmisibila; ca urmare, numai directiile p care fac unghiuri mai mari de 90° cu
ambii vectori 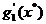 si
si  reprezinta directii
admisibile.
reprezinta directii
admisibile.
Conform cu (2.13), pentru ca vectorul directiei admisibile p sa faca unghiuri mai mari de
90° cu vectorii 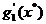 si
si  sunt necesare conditiile
sunt necesare conditiile
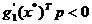 ;
; 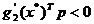 . (2.31)
. (2.31)
Pe de alta parte, din relatia (2.13) a rezultat ca pentru ca
o directie p sa asigure
descresterea functiei criteriu f(x) este necesar ca vectorul p sa faca un unghi mai mic de
90° cu vectorul gradient 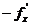 .
.
Ca urmare, daca sunt respectate conditiile Kuhn-Tucker si
vectorul - se gaseste intre vectorii
se gaseste intre vectorii 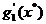 si
si  - conform relatiei
(2.30) si Fig. 3.1 - atunci nu va exista nici o directie p care sa faca un unghi de pana
la 90° cu vectorul -
- conform relatiei
(2.30) si Fig. 3.1 - atunci nu va exista nici o directie p care sa faca un unghi de pana
la 90° cu vectorul - si in acelasi timp sa poata face
unghiuri de peste 90° cu ambii vectori
si in acelasi timp sa poata face
unghiuri de peste 90° cu ambii vectori 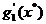 si
si  (deoarece orice directie
p care face unghiuri mai mari de 90°
cu ambii vectori
(deoarece orice directie
p care face unghiuri mai mari de 90°
cu ambii vectori 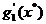 si
si  va face un unghi mai
mare de 90° si cu vectorul -
va face un unghi mai
mare de 90° si cu vectorul - , aflat intre cei doi vectori), deci nu va exista nici o
directie admisibila care sa conduca la descresterea
functiei criteriu: in consecinta, punctul E reprezinta punctul de optim (minim) cu restrictii.
, aflat intre cei doi vectori), deci nu va exista nici o
directie admisibila care sa conduca la descresterea
functiei criteriu: in consecinta, punctul E reprezinta punctul de optim (minim) cu restrictii.
Trecand la cazul general n-dimensional
in prezenta a r restrictii,
conditia (2.30) capata aspectul
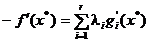 (2.32)
(2.32)
cu  .
.
Conditia ca vectorul - sa se gaseasca intre vectorii
sa se gaseasca intre vectorii 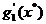 si
si  este evident
echivalenta cu conditia ca vectorul
este evident
echivalenta cu conditia ca vectorul  sa se gaseasca
intre vectorii -
sa se gaseasca
intre vectorii -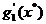 si -
si - , deci conditia generala (2.32) poate fi pusa si
sub forma
, deci conditia generala (2.32) poate fi pusa si
sub forma
 , (2.33)
, (2.33)
cu  .
.
Pe langa relatia (2.32) sau (2.33), formularea conditiilor
Kuhn-Tucker include si o relatie de forma
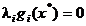 (2.34)
(2.34)
explicata in
[Las75]
Conditiile Kuhn-Tucker sunt folosite in numeroase metode de optimizare
cu restrictii pentru generarea de directii de deplasare spre optim
(sau pentru stabilirea unor criterii de oprire a cautarii atunci cand
verificarea conditiilor Kuhn-Tucker atesta atingerea optimului.
3. Folosirea functiilor de penalizare pentru
optimizarea cu restrictii
Metoda functiilor de penalizare permite transformarea problemelor de
optimizare cu restrictii egalitate si inegalitate in probleme de
optimizare fara restrictii. Astfel, presupunand ca se urmareste
minimizarea functiei criteriu f(x), cu restrictiile
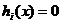 , i = 1, 2, , m (2.35)
, i = 1, 2, , m (2.35)
si
 , j = 1, 2, , r (2.36)
, j = 1, 2, , r (2.36)
Se poate obtine o varianta a functiilor de penalizare
transformand in prealabil restrictiile inegalitate (2.36) in restrictii
egalitate cu ajutorul unor variabile auxiliare kj, scriind restrictiile egalitate echivalente
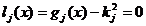 , (2.37)
, (2.37)
(transformare
analoaga cu cea din (2.18), intervenind insa semnul minus datorita
deosebirii dintre (2.17) si (2.36), respectiv dintre caracterul restrictiilor
inegalitate) si cautand apoi minimul fara restrictii
al functiei
 . (2.38)
. (2.38)
unde functiile
 si
si  sunt functii de penalizare, care trebuie
sa satisfaca anumite conditii, iar
sunt functii de penalizare, care trebuie
sa satisfaca anumite conditii, iar 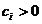 si
si 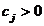 sunt factori de ponderare. In cel mai simplu
caz se poate adopta
sunt factori de ponderare. In cel mai simplu
caz se poate adopta
 (2.39)
(2.39)
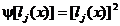 (2.40)
(2.40)
si relatia
(2.38) capata forma
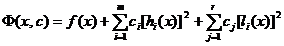 (2.41)
(2.41)
Din (3.41) se constata ca daca restrictiile (2.35) si
(2.37) sunt satisfacute - ceea ce inseamna ca sunt satisfacute
restrictiile initiale (2.35) si (2.36) - atunci functiile 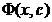 si f(x)
devin egale si deci minimizarea functiei
si f(x)
devin egale si deci minimizarea functiei 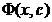 asigura minimul
functiei criteriu f(x).
asigura minimul
functiei criteriu f(x).
Daca unele din restrictiile (2.35) sau (2.37) sunt incalcate
si daca sunt alese valori suficient de mari pentru factorii de
ponderare ci si cj atunci, chiar la abateri
mici ale functiilor  si
si  de la valoarea zero rezulta cresteri
mari ale valorii functiei
de la valoarea zero rezulta cresteri
mari ale valorii functiei 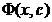 - deci nu se poate obtine
un minim al acestei functii - si prin urmare procesul de cautare
este fortat sa revina in domeniul in care restrictiile sunt
respectate.
- deci nu se poate obtine
un minim al acestei functii - si prin urmare procesul de cautare
este fortat sa revina in domeniul in care restrictiile sunt
respectate.
O varianta a functiilor de penalizare utilizata relativ
frecvent a fost elaborata de Fiacco si McCormick [Cal79]. Considerand minimizarea functiei
criteriu f(x), cu restrictiile
 , (2.42)
, (2.42)
se cauta
printr-un proces secvential minimizarea fara restrictii a functiei
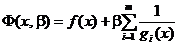 (2.43)
(2.43)
unde procesul de
minimizare se repeta pentru diferite valori descrescatoare ale
factorului b 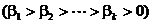 .
.
Din (3.43) se constata ca minimul functiei  va rezulta in
interiorul domeniului admisibil delimitat de restrictiile (3.42), intrucat
pe frontiera acestui domeniu se obtine
va rezulta in
interiorul domeniului admisibil delimitat de restrictiile (3.42), intrucat
pe frontiera acestui domeniu se obtine  si functia
si functia  tinde sa creasca
spre infinit, deci nu poate rezulta un
minim.
tinde sa creasca
spre infinit, deci nu poate rezulta un
minim.
Intrucat metoda presupune apropierea de optim din interiorul domeniului
admisibil delimitat de restrictii, punctul initial al procesului
secvential trebuie sa se gaseasca in interiorul domeniului
admisibil; cautarea unui punct din domeniul admisibil este prezentata
in [Bri05].
Datorita caracterului secvential, metoda a fost denumita
'tehnica de minimizare secven-tiala fara restrictii'
(in limba engleza: sequential unconstrained minimization technique SUMT).
In ultimii ani, metoda functiilor de penalizare a fost combinata
cu metoda multiplicatorilor Lagrange in cadrul metodei lagrangeanului extins [Cal79]; pentru minimizarea unei functii
criteriu f(x) cu restrictiile
 , j = 1, 2, , r (2.44)
, j = 1, 2, , r (2.44)
se folosesc
variabile auxiliare si se transforma, problema data, intr-o
problema de minimizare a functiei f(x) cu restrictiile echivalente
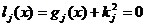 , (2.45)
, (2.45)
optimul fiind
obtinut prin minimizarea fara restrictii a functiei
L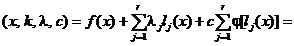
 (2.46)
(2.46)
aceasta functie
reprezentand lagrangeanul extins. Functia 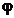 este o functie de
penalizare si din (2.46) se constata ca in expresia
lagrangeanului extins intervin atat termeni corespunzatori metodei
multiplicatorilor Lagrange - de tipul celor din (2.3) - cat si termeni
corespunzatori functiilor de penalizare, de tipul celor din (2.38).
este o functie de
penalizare si din (2.46) se constata ca in expresia
lagrangeanului extins intervin atat termeni corespunzatori metodei
multiplicatorilor Lagrange - de tipul celor din (2.3) - cat si termeni
corespunzatori functiilor de penalizare, de tipul celor din (2.38).
4. Metode specifice de optimizare cu
restrictii
Metodele de optimizare cu restrictii mentionate in acest paragraf
sunt denumite specifice in sensul ca nu fac apel la transformari ale
problemelor de optimizare cu restrictii in probleme de optimizare fara
restrictii.
Principalele metode specifice se bazeaza pe generarea directiilor
admisibile, respectiv a directiilor caracterizate de faptul ca
efectuarea unor deplasari mici nu incalca restrictiile. Daca
o astfel de deplasare asigura si o apropiere de extrem (de exemplu,
asigura micsorarea functiei criteriu in cazul cautarii
unui minim), atunci directia admisibila este o directie
admisibila si utilizabila.
Cele mai frecvent folosite metode bazate pe generarea directiilor
admisibile sunt cele elaborate de Zoutendijk si de Rosen.
In cadrul metodei Zoutendijk [Cal79],
pentru minimizarea functiei criteriu f(x) cu restrictii de forma
 , j = 1, 2, , r (2.47)
, j = 1, 2, , r (2.47)
se genereaza
directii admisibile p, care -
conform celor mentionate in paragraful 2.2 - trebuie sa faca
unghiuri mai mari de 90° cu toti gradientii restrictiilor  , respectiv trebuie sa satisfaca relatii de
forma (3.31):
, respectiv trebuie sa satisfaca relatii de
forma (3.31):
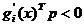 , i = 1, 2, , r. (2.48)
, i = 1, 2, , r. (2.48)
Pe de alta parte, pentru ca directiile admisibile sa fie si
utilizabile, ele trebuie sa asigure descresterea functiei
criteriu f(x), deci trebuie sa satisfaca o conditie de forma (1.13)
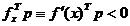 . (2.49)
. (2.49)
Ca urmare, metoda include un algoritm care la fiecare iteratie
selecteaza o directie admisibila si utilizabila,
asigurand satisfacerea ambelor relatii (2.48) si (2.49), deci conducand
totodata la descresterea functiei criteriu si la departarea
de granitele domeniilor interzise, fixate prin restrictiile (2.47).
In cadrul metodei Rosen [Cal79], directiile
admisibile sunt obtinute prin intermediul utilizarii conditiilor
Kuhn-Tucker, care intervin si in criteriul de oprire a procesului de cautare
la atingerea optimului. Metoda este indicata indeosebi pentru cazul
restrictiilor liniare
 , j = 1, 2, , r, (2.50)
, j = 1, 2, , r, (2.50)
care pot fi puse
sub forma
 , (2.51)
, (2.51)
respectiv
 (2.52)
(2.52)
Ecuatiile care corespund limitei domeniilor admisibile definite de
restrictiile (2.52) au aspectul 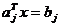 si corespund unor hiperplane.
si corespund unor hiperplane.
Directiile de cautare sunt generate iterativ prin proiectia
vectorului -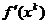 pe intersectia hiperplanelor care trec prin punctul
curent xk, iar daca
prin xk nu trec asemenea
hiperplane (cand punctul x se gaseste
in interiorul domeniului admisibil) directia deplasarii este
constituita chiar de gradientul cu semn schimbat -
pe intersectia hiperplanelor care trec prin punctul
curent xk, iar daca
prin xk nu trec asemenea
hiperplane (cand punctul x se gaseste
in interiorul domeniului admisibil) directia deplasarii este
constituita chiar de gradientul cu semn schimbat -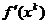 .
.
Datorita procedeului de generare a directiilor, metoda este
denumita metoda proiectiei gradientului.
5. Folosirea conditiilor Karush-Kuhn-Tucker pentru optimizarea cu restrictii
Pentru rezolvarea problemelor de optimizare convexe cu restrictii de
tip inegalitate se poate folosi metoda Karush-Kuhn-Tucker (KKT) [Bri05]. Aceasta metoda apartine
metodelor de programare neliniara si ofera un optim global in
domeniul admisibil al functiei criteriu corespunzatoare problemei
formulate.
Formularea problemei. Fie 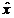 un punct din
spatiul
un punct din
spatiul  si
si  ,
,  , functii continue de n variabile definite pe o sfera deschisa cu centrul in
, functii continue de n variabile definite pe o sfera deschisa cu centrul in 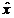 , astfel incat
, astfel incat  ,
,  . Sa se determine minimul functiei f, cu restrictiile
. Sa se determine minimul functiei f, cu restrictiile 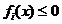 ,
,  .
.
Solutia problemei utilizeaza metoda multiplicatorilor Lagrange
si este data de:
Teorema Karush-Kuhn-Tucker. Se defineste functia
L L
L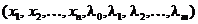
 , cu
, cu 
numita
functie Lagrange atasata problemei formulate, in care 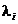 ,
,  sunt multiplicatorii
Lagrange. Presupunem ca toate functiile
sunt multiplicatorii
Lagrange. Presupunem ca toate functiile 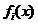 ,
,  sunt
diferentiabile in
sunt
diferentiabile in 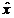 . Conditiile Karush-Kuhn-Tucker raman valabile in
punctul
. Conditiile Karush-Kuhn-Tucker raman valabile in
punctul 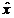 pentru o selectie
nenula a multiplicatorilor Lagrange
pentru o selectie
nenula a multiplicatorilor Lagrange  , cu
, cu  , daca sunt indeplinite urmatoarele conditii:
, daca sunt indeplinite urmatoarele conditii:
(a)
L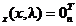 (conditia Lagrange de stationaritate);
(conditia Lagrange de stationaritate);
(b)
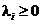 ,
,  (conditiile de
nenegativitate);
(conditiile de
nenegativitate);
(c)
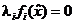 ,
,  (conditiile de
stationaritate complementara - lipsa de energie)
(conditiile de
stationaritate complementara - lipsa de energie)
Observatie. Diferenta esentiala
fata de conditiile Lagrange consta in ne-negativitatea
multiplicatorilor Lagrange. Pentru o conditie de stagnare
complementara, de exemplu a i-a conditie, presupune doua cazuri:
fie 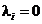 , fie
, fie  . Rezulta astfel un total de
. Rezulta astfel un total de 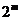 cazuri.
cazuri.
Inainte de a prezenta suficienta
conditiilor KKT formulate mai sus, precizam ca un punct  se numeste punct Slater daca
se numeste punct Slater daca  ,
,  .
.
Suficienta conditiilor KKT.
(i) Conditiile KKT sunt suficiente pentru optimalitate, cu conditia
ca 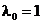 . Mai exact, daca conditiile KKT sunt valabile
intr-un punct
. Mai exact, daca conditiile KKT sunt valabile
intr-un punct 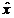 pentru o selectie
a multiplicatorilor Lagrange
pentru o selectie
a multiplicatorilor Lagrange  , cu
, cu 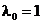 , atunci
, atunci 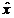 este un punct de
minim. (ii) Presupunem ca exista un punct Slater. Daca
conditiile KKT sunt valabile pentru o selectie a multiplicatorilor
Lagrange
este un punct de
minim. (ii) Presupunem ca exista un punct Slater. Daca
conditiile KKT sunt valabile pentru o selectie a multiplicatorilor
Lagrange  , atunci
, atunci  nu poate fi zero.
nu poate fi zero.
Pentru claritate, in cele ce urmeaza
vom prezenta cateva exemple de aplicare a teoremei KKT.
Exemplul 2.1. Sa se gaseasca punctul  cel mai apropiat de
punctul (2, 3) cu conditiile ca: (a) suma coodonalelor acestuia sa nu
depaseasca valoarea 2, (b) valoarea absoluta a primei
coordonate sa nu depaseasca valoarea 2.
cel mai apropiat de
punctul (2, 3) cu conditiile ca: (a) suma coodonalelor acestuia sa nu
depaseasca valoarea 2, (b) valoarea absoluta a primei
coordonate sa nu depaseasca valoarea 2.
Solutie. Problema poate fi modelata ca o
problema de minimizare cu restrictii de tip inegalitate, astfel:
sa se minimizeze functia 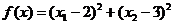 cu restrictiile
cu restrictiile 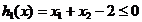 ,
, 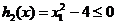 .
.
Pentru rezolvarea problemei utilizam teorema KKT. Definim functia
Lagrange
L
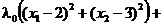
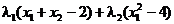 (3.54)
(3.54)
in care vom
considera 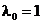 (Atentie, punctul
(0, 0) este un punct Slater).
(Atentie, punctul
(0, 0) este un punct Slater).
Conditiile KKT:
 L
L
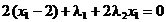 (2.55)
(2.55)
 L
L
 (2.56)
(2.56)
 (2.57)
(2.57)
 (2.58)
(2.58)
 (2.59)
(2.59)
Cazul 1: constrangerile impuse nu sunt "etanse",
adica 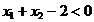 si
si 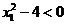 . In aceasta situatie conditiile KKT
anterioare se rescriu sub forma:
. In aceasta situatie conditiile KKT
anterioare se rescriu sub forma:
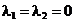 ,
,  ,
, 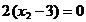
din care rezulta punctul 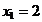 ,
, care insa nu este un punct admisibil, intrucat nu
satisface conditia
care insa nu este un punct admisibil, intrucat nu
satisface conditia 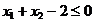 .
.
Cazul 2: numai a doua constrangere este
"etansa", adica 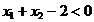 si
si  . In aceasta situatie conditiile KKT definite
mai sus se rescriu sub forma:
. In aceasta situatie conditiile KKT definite
mai sus se rescriu sub forma:
 ,
,  ,
,  ,
, 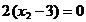

din care
rezulta punctul 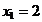
 care insa, ca
si in cazul 1, nu este un punct admisibil.
care insa, ca
si in cazul 1, nu este un punct admisibil.
Cazul 3: numai prima constrangere este
"etansa", adica  si
si 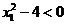 . In aceasta situatie conditiile KKT definite
mai sus se rescriu sub forma:
. In aceasta situatie conditiile KKT definite
mai sus se rescriu sub forma:
 ,
, 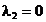 ,
, 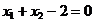 ,
, 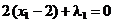

din care rezulta punctul 
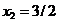 , cu
, cu  . Acesta este un punct admisibil (satiface restrictiile
impuse) si reprezinta un punct de optim global. Deci,
. Acesta este un punct admisibil (satiface restrictiile
impuse) si reprezinta un punct de optim global. Deci, 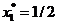
 , pentru care
, pentru care 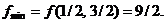 ,
,
La acest pas ne putem opri, deoarece am gasit o solutie care este
unica. Unicitatea solutiei rezulta din convexitatea stricta
a functiei obiectiv.
Conditiile KKT sunt satisfacute pentru urmatoarele valori
ale multiplicatorilor Lagrange: 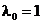 ,
,  ,
, 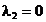 .
.
Exemplul 2.2. Sa se gaseasca punctul  care este cel mai
apropiat de punctul de coordonare (2, 3) cu conditiile ca: (a) valoarea
primei coordonate
care este cel mai
apropiat de punctul de coordonare (2, 3) cu conditiile ca: (a) valoarea
primei coordonate 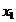 sa fie cel
putin 1, (b) punctul
sa fie cel
putin 1, (b) punctul  se afla pe un
cerc cu centrul in origine si de raza 2.
se afla pe un
cerc cu centrul in origine si de raza 2.
Solutie. Problema poate fi modelata ca o
problema de minimizare cu restrictii de tip inegalitate, astfel:
sa se minimizeze functia 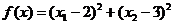 cu restrictiile
cu restrictiile 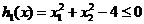 ,
, 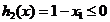 .
.
Pentru rezolvarea problemei utilizam Teorema KKT. Definim functia
Lagrange
L
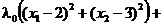
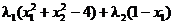 (2.60)
(2.60)
in care vom
considera 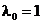 (Atentie, punctul
(3/2, 0) este un punct Slater).
(Atentie, punctul
(3/2, 0) este un punct Slater).
Conditiile KKT:
 L
L
 (2.61)
(2.61)
 L
L
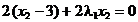 (2.62)
(2.62)
 (2.63)
(2.63)
 (2.64)
(2.64)
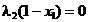 (2.65)
(2.65)
Cazul 1: constrangerile impuse nu sunt
"etanse", adica 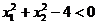 si
si  . In aceasta situatie conditiile KKT
anterioare se rescriu sub forma:
. In aceasta situatie conditiile KKT
anterioare se rescriu sub forma:
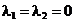 ,
, 
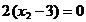
din care
rezulta punctul 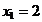
 care insa nu este un punct admisibil,
intrucat nu satisface restrictia
care insa nu este un punct admisibil,
intrucat nu satisface restrictia 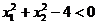 .
.
Cazul 2: numai a doua constrangere este
"etansa", adica 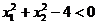 si
si 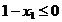 . In aceasta situatie, conditiile KKT definite
mai sus se rescriu sub forma:
. In aceasta situatie, conditiile KKT definite
mai sus se rescriu sub forma:
 ,
,  ,
,  ,
, 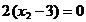

din care
rezulta punctul 
 ,
, 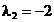 care insa, ca
si in cazul 1, nu este un punct admisibil si mai mult,
care insa, ca
si in cazul 1, nu este un punct admisibil si mai mult, 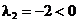 .
.
Cazul 3: numai prima constrangere este
"etansa", adica  si
si 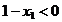 . In aceasta situatie conditiile KKT definite
mai sus se rescriu sub forma:
. In aceasta situatie conditiile KKT definite
mai sus se rescriu sub forma:
 ,
, 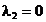 ,
,  ,
, 
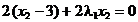
din care rezulta punctul 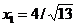
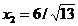 , cu
, cu  . Acesta este un punct admisibil (satiface restrictiile
impuse) si reprezinta un punct de optim global. Deci,
. Acesta este un punct admisibil (satiface restrictiile
impuse) si reprezinta un punct de optim global. Deci, 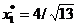
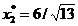 , pentru care
, pentru care 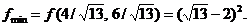
Conditiile KKT sunt satisfacute
pentru urmatoarele valori ale multiplicatorilor Lagrange: 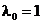 ,
,  ,
, 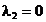 .
.
Observatie. Se putea merge si pe
"intuitie", in sensul ca punctul cautat trebuie sa se
gaseasca pe cercul  , iar coordonata
, iar coordonata 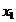 sa satisfaca conditia
sa satisfaca conditia 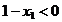 , care de fapt reprezinta cazul 3 prezentat mai
anterior.
, care de fapt reprezinta cazul 3 prezentat mai
anterior.


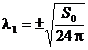

 ,
,  (2.16)
(2.16)