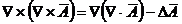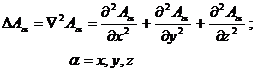Relatii din analiza vectoriala

Relatii din analiza vectoriala

Produsul scalar a doi vectori:

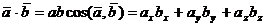
Produsul vectorial a doi vectori:

;   

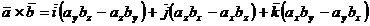
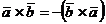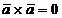
Produsul mixt a trei vectori:

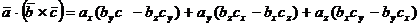
Produsul vectorial a trei vectori:

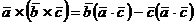
-Rezultatul aplicarii operatorului lui Laplace, 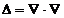, egal cu produsul scalar a doi operatori nabla asupra unei functii scalare f, este scalarul:

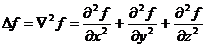
(in coordonate carteziene).

-Rezultatul aplicarii operatorului Laplace, D, asupra unui vector 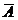, conduce la trei ecuatii scalare:

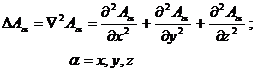
(in coordonate carteziene).

Teorema lui Gauss:

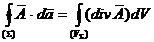
Teorema lui Stokes:

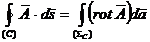
Rotorul gradientului oricarei functii scalare este nul:

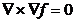
Divergenta rotorului oricarui vector este nula:

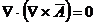
Gradientul unei sume:

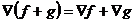
Gradientul unui produs:

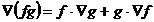
Divergenta sumei a doi vectori:

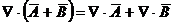
Divergenta produsului unui scalar cu un vector:

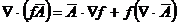
Divergenta produsului vectorial a doi vectori:

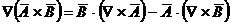
Rotorul sumei a doi vectori:

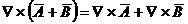
Rotorul produsului unui scalar cu un vector:

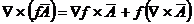
Rotorul rotorului unui vector: