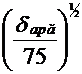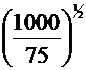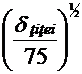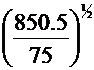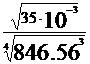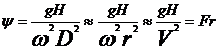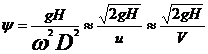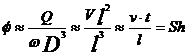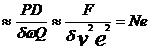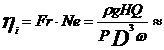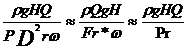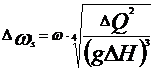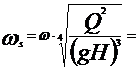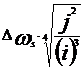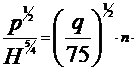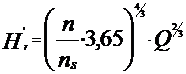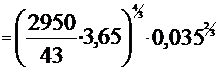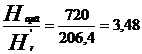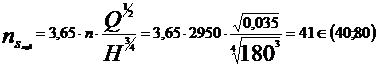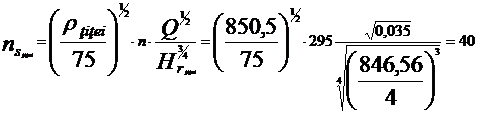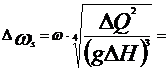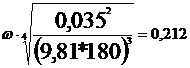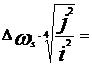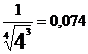1 Breviar de calcul tehnologic si
functional
Pentru
transportul unui amestec de titei B si C in proportii egale
se va proiecta o pompa centrifuga care la o turatie a arborelui
n = 2950
rot/min sa
realizeze debitul de refulare Qr = 120 m3/h. Temperatura de
lucru t = 5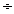 300C.
Amestecul de titei
va fi transportat printr-o retea de conducte unui numar de 4
consumatori conform figurii
300C.
Amestecul de titei
va fi transportat printr-o retea de conducte unui numar de 4
consumatori conform figurii
Fig. 1.1
Schema instalatiei
in care sunt cunoscute:
-
lungimile L0-1 = 10000 m L4-5
= 1500 m
L1-2 = 4000 m L4-6 = 1500 m
L1-3 = 2000 m L3-7
= 4000 m
L3-4 = 1500
m L0-8 =
10
-
debitele pe fiecare troson
Q0-1 = Qr = Q1 + Q2
+ Q3 + Q4 = 120 m3/h
= 33.3 · 10-3 m3/s
Q1-2 = Q1 = 40 m3/h
=11.11 · 10-3 m3/s
Q4-6 = Q2 = 20 m3/h
= 5.55 · 10-3 m3/s =5.55 l/s
Q4-5 = Q3 = 20 m3/h
= 5.55 · 10-3 m3/s
Q3-7
= Q4 = 40 m3/h = 11.11 · 10-3 m3/s
cotele de amplasare
z0 = 595 m z2 = 800 m z5 = 700 m
z8 = 600 m z3 =
620 m z6 =
700 m
z1 = 610 m z4 = 640 m z7 = 756.2 m
presiunea la consumatori : p =3 bor = 3 · 105 N/m2
titeiul 3 face parte
din categoria titeiurilor semiparafinoase
ζ8 = 860 [kg/m3 ]
titeiul C face parte
din categoria titeiurilor parafinoase
ζc = 841 [kg/m3 ]
2.
Determinarea parametrilor functionali ai pompei
Stabilirea
diametrelor optime ale conductelor .
Debitul intrat in rotor este dat de suma
debitului din conductorul de refulare.
Qef
= Qr = Q0+1 si cantitatea de lichid pierdut " Q " neetanseitati
Q " neetanseitati
Qa
= Qef +  Q = (403
Q = (403 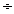 1.1 ) · Qef
1.1 ) · Qef
Qa = 1.05·120 =126 [m3/h ] =35 · 10-3
m3/s = 35 l/s
In aceste conditii expresia
randamentului va fi
v = Qef/
Qa = Qef/ Qef + 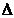 Q = 0.90
Q = 0.90 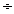
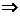 v
v 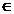 ( 0.90
( 0.90 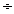
Se recomanda viteza titeiului pe conducta de aspiratie
Va 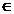 [1.5
[1.5 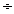 2.5(3)] m/s
2.5(3)] m/s
Se adopta Va = 1 m/s si Vr = 2 m/s
Densitatea
amestecului de titei va fi
ρom = 0.5 ·
ρB + 0.5 · ρC =0.5 · 860 + 0.5 · 841
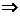 ρom =
850.5 kg/m3
ρom =
850.5 kg/m3
Vascozitatea cinematica a celor
doua titeiuri este :
- la t = 50C 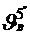 = 25 cSt =25 · 10-6 m2/s
= 25 cSt =25 · 10-6 m2/s

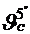 = 19 cSt =18 · 10-6 m2/s
= 19 cSt =18 · 10-6 m2/s
- la t= 300C 
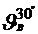 = 9.45 cSt =9.45·10-6
m2/s
= 9.45 cSt =9.45·10-6
m2/s
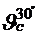 = 7.75cSt =7.75·10-6 m2/s
= 7.75cSt =7.75·10-6 m2/s
Vascozitatea amestecului de titei va fi
- la t = 50C 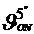 = 10.2 cSt =10.2·10-6
m2/s
= 10.2 cSt =10.2·10-6
m2/s
- la t= 300C 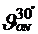 = 6.6 cSt =6.6·10-6 m2/s
= 6.6 cSt =6.6·10-6 m2/s
Diametrul conductelor se va determina
din formula debitului de titei ce trece prin conducta
Q=
A· v =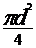 · v
· v 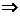 d=
d= 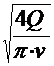
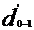
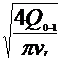
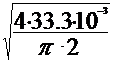 = 0.14566 m =145.6 mm.
= 0.14566 m =145.6 mm.
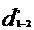
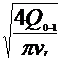
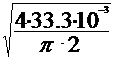 = 0.0841 m =81 mm.
= 0.0841 m =81 mm.
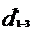
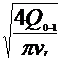
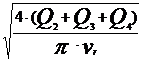 = 0.11893 m =118.93 mm.
= 0.11893 m =118.93 mm.
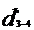
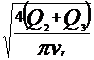
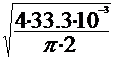 = 0.0841 m =81 mm.
= 0.0841 m =81 mm.
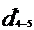

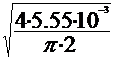 = 59.44·10-3 m =59.44 mm.
= 59.44·10-3 m =59.44 mm.
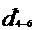
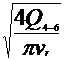
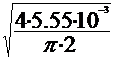 = 59.44·10-3 m =59.44 mm.
= 59.44·10-3 m =59.44 mm.
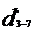
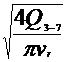
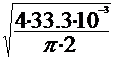 = 0.0841 m =81 mm.
= 0.0841 m =81 mm.
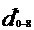
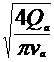
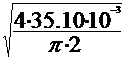 = 0.211 m =211 mm.
= 0.211 m =211 mm.
Diametrele interioare ale conductelor se aleg conform
STAS 715/8 - 88.
Caracteristicile conductelor
|
Tronson
|
Diametrul
interior
|
Diametrul
exterior
|
Grosimea
de perete
|
Masa
liniara
|
|
[ mm ]
|
[mm]
|
[ in ]
|
[ mm ]
|
[kg/m]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cu aceste
valori ale diametrelor se vor recalcula vitezele titeiului pe fiecare
conducta
V0-1= 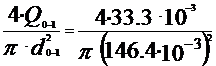 =1.98 m/s
=1.98 m/s
V1-2=  =1.94 m/s
=1.94 m/s
V1-3= 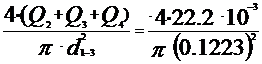 =1.89 m/s
=1.89 m/s
V3-4= 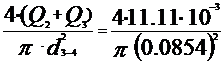 =1.94 m/s
=1.94 m/s
V4-5= 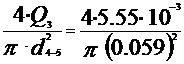 =2.03 m/s
=2.03 m/s
V4-6 = 2.03 m/s
V3-7= 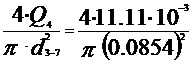 =1.94 m/s
=1.94 m/s
V0-8= 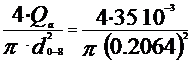 =1.04 m/s
=1.04 m/s
Cu aceste valori ale vitezelor titeiului prin conducte vom calcula
numarul lui Reynolds, care reprezinta raportul dintre fortele de
inertie si cele de vascozitate,cu formula :
Re = 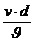 , si are o imprtanta foarte mare in studiul
miscarii fluidelor vascoase.
, si are o imprtanta foarte mare in studiul
miscarii fluidelor vascoase.
A.
- la
temperatura t= 50C
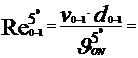 28418,82 < 105
28418,82 < 105
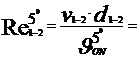 16242.74 < 105
16242.74 < 105
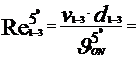 22661.47 < 105
22661.47 < 105
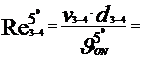 16242.74 < 105
16242.74 < 105
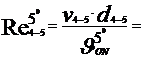 11742.15 < 105
11742.15 < 105
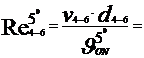 11742.15 < 105
11742.15 < 105
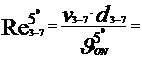 16242.74 < 105
16242.74 < 105
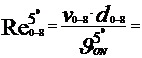 21047 < 105
21047 < 105
A.
- la temperatura
t= 300C
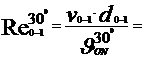 43920.0 < 105
43920.0 < 105
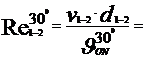 25102.42 < 105
25102.42 < 105
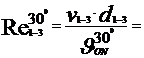 35022.27 < 105
35022.27 < 105
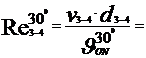 25102.42 < 105
25102.42 < 105
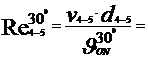 18146.97 < 105
18146.97 < 105
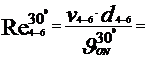 18146.97 < 105
18146.97 < 105
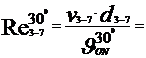 25102.42 < 105
25102.42 < 105
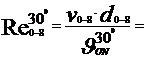 32523.63 < 105
32523.63 < 105
Cum numarul lui Reynolds depaseste valoarea critica Re =
2300,
Regimul de curgere prin conducte este
turbulent. In acest regim cu ajutorul formulei lui Blasius, valabila
pentru Re <105, vom determina coeficientii de vascozitate
hidraulica:

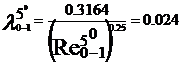
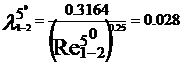
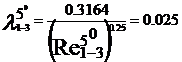
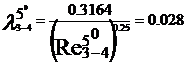

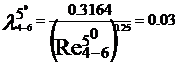
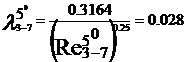
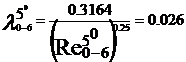
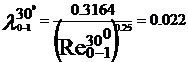
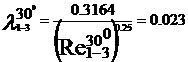
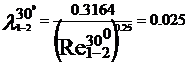

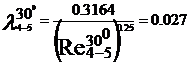
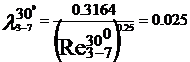
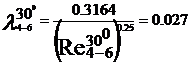
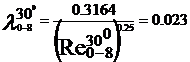
Rezultatele precedente pot
fi utilizate atat timp cat peretele interior al tubului este neted. In acest
caz, starea peretelui nu are nici o influenta asupra formelor legii
miscarilor turbulente. Din cauza rugozitatii peretelui,
rezistenta este mai mare decat aceea care rezulta din formulele
precedente pentru tuburile netede.
S-a ajuns la concluzia ca exista doua tipuri de
rugozitati. La primul dintre acestea, rezistenta este
proportionala cu patratul vitezei medii, ceea ce inseamna
ca 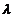 este independent de numarul lui Reynolds. Influenta
peretelui se poate caracteriza in acest caz printr-un singur parametru de
rugozitate:
este independent de numarul lui Reynolds. Influenta
peretelui se poate caracteriza in acest caz printr-un singur parametru de
rugozitate: 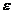 = k/ro = 2k/d, numit rugozitate relativa, in
care k este inaltimea rugozitatilor, d diametrul interior
al conductei.
= k/ro = 2k/d, numit rugozitate relativa, in
care k este inaltimea rugozitatilor, d diametrul interior
al conductei.
Cel de-al doilea tip de rugozitate se intalneste atunci cand
rugozitatile peretelui sunt mai reduse sau cand putine
rugozitati izolate se afla repartizate pe o suprafata
neteda destul de mare, cum ar fi, de exemplu, tevile de lemn sau
tevile din fier comerciale uzuale.
Pierderea de sarcina totala hr
datorita rezistentelor hidraulice din conducta este data de
expresia: hh = hh1
+ hh2, unde hh1 - pierderile liniare, se produc pe portiunea
dreapta a conductei si se calculeaza cu formula hh1 =
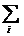 λi · Li/di ·
λi · Li/di · 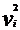 /2g, in care:
/2g, in care:
L - lungimea conductei [m]
d diametrul interior al conductei [m]
v - viteza medie in
conducta [m/s], v 4Q/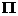 ·d2
·d2
- coeficient de
pierdere linara
hh2 - pierderi
locale, care provin din variatiile de viteze sau din
schimbarile de directie a curentului de fluid, astfel: la intrarea
si iesirea din conducta, la cresteri sau reduceri de
sectiuni, la coturi, vane, etc.
hh2 = 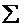
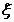 i ·
i · 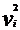 /2g
/2g
inlocuind obtinem
hh
= 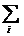 (λi · Li/di -
(λi · Li/di -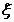 i) ·
i) · 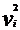 /2g
/2g
Pentru regim de curgere turbulent, distributia vitezei este
diferita de o parabola datorita faptului ca peste
miscarea in directia axei conductei, care este miscarea principala,
se suprapun miscari transversale la scara microscopica,
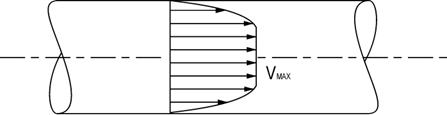
fenomen caracteristic curgerii turbulente. In acest caz turbulenta face ca distributia
vitezei intr-o sectiune transversala sa fie mai uniforma
avand forma unei parabole turtite.
Fig. 2.2 Distributia de
viteze intr-o sectiune transversala in cazul curgerii turbulente
Viteza medie se calculeaza cu relatia :
Vmed = (0.7 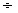 0.9) Vmax
0.9) Vmax
Daca viteza fluidului
din conducta este moderata, atunci substratul laminar poate deveni de
o asemenea grosime incat sa acopere toate asperitatile
conductei. In acest caz conducta se considera "neteda" din punct de
vedere hidraulic. Cand insa
substratul laminar acopera doar o parte din asperitati, conducta
se considera "mixta" din punct de vedere hidraulic. In cazul unor
viteze mari, fluidul din conducta poate antrena intregul substrat laminar,
astfel incat toate asperitatile conductei intra in curentul
principal, conducta se considera "rugoasa" din punct de vedere
hidraulic.
O conducta neteda
poate deveni mixta sau rugoasa pe doua cai:
instantaneu, cresterea brusca a
debitului duce la cresterea vitezei si aceasta la miscarea
substratului laminat si cum asperitatile au anumite valori, se poate
trece de la starea neteda la cea mixta sau rugoasa.
in timp, asa cum este cazul conductelor
in exploatare cand debitul se poate mentine constant, insa
asperitatile crescand vor patrunde treptat in curentul principal,
conducta trecand inevitabil de la starea neteda la cea rugoasa sau
mixta.
Pentru cazul cel mai
nefavorabil, la t 5oC

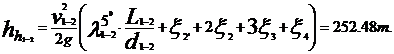
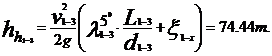
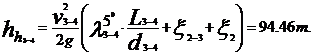
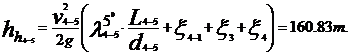
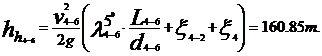
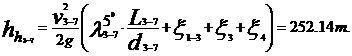

La
temperatura t=300C
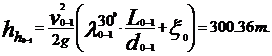
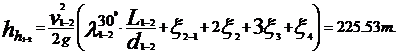
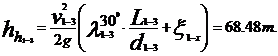
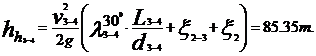
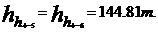
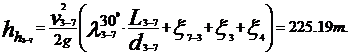
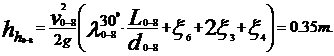
3 Stabilirea inaltimii de pompare a pompei centrifuge in
functie de elementele exterioare pompei
Pentru functionarea corecta a ansamblului pompa
centrifuga-retea, dimensionarea pompei centrifuge se face punand
conditia ca inaltimea de pompare determinata in
functie de debit si elementele exterioare sa fie egala cu
inaltimea creata de pompa pentru debitul vehiculat.
Pentru exprimarea inaltimii de
pompare in functie de elementele retelei se aplica ecuatia
lui Bernoulli atat pentru traseul de aspiratie cat si pentru cel de
refulare. In ipoteza ca nivelul lichidului din cele doua vase
(aspiratie si refulare) ramane constant ceea ce corespunde
proceselor tehnologice continue, viteza lichidului din vasele mentionate este nula .In
aceste conditii se obtine inaltimea de pompare
exprimata in functie de elementele retelei.
H= (p2 - p2)/(g· )+Hg +∑hh .
unde Hg = Hr + Ha + 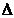 Z - diferenta de
nivel intre suprafata libera a lichidului din rezervorul superior
si inferior, numita si inaltime geodezica [m] .
Z - diferenta de
nivel intre suprafata libera a lichidului din rezervorul superior
si inferior, numita si inaltime geodezica [m] .
∑hh ∑hhr
+ ∑hha - suma
tuturor pierderilor hidraulice pe circuitul parcurs de lichidul vehiculat
∑hh = ∑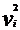 /2g·(λI · Li/di
+∑ξij )
/2g·(λI · Li/di
+∑ξij )
H6 = 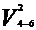 /2g + P6/γ + (Z6 - Z8)
=(2.032/2·9.81) + (3·105/9.81·850.5) + 100 = 136.16 m
/2g + P6/γ + (Z6 - Z8)
=(2.032/2·9.81) + (3·105/9.81·850.5) + 100 = 136.16 m
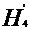 = H6 + hh4-6
= 136.16+160.85 =297.01 m
= H6 + hh4-6
= 136.16+160.85 =297.01 m
H5 = 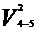 /2g + P5/γ + (Z5 - Z8)
= 136.16
/2g + P5/γ + (Z5 - Z8)
= 136.16
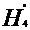 = H5 + hh4-5
= 136.16+160.83 =296.99 m
= H5 + hh4-5
= 136.16+160.83 =296.99 m
H4 = max (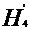 ;
;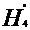 ) = 297,01 m
) = 297,01 m
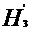 = H4 + hh3-4=
297.01+946 =391.47
= H4 + hh3-4=
297.01+946 =391.47
H7 = 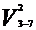 /2g + P7/γ + (Z7 - Z8)
=( 1.94/2·9.81) + ( 3·105/9.81·850.5 ) + 156.2 = 192.33 m
/2g + P7/γ + (Z7 - Z8)
=( 1.94/2·9.81) + ( 3·105/9.81·850.5 ) + 156.2 = 192.33 m
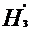 = H7 + hh3-7=
192.33 + 252.14 =4447 m
= H7 + hh3-7=
192.33 + 252.14 =4447 m
H3 = max (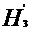 ;
;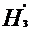 ) = 4447
) = 4447
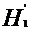 = H3+ hh1-3
= 4447 + 744 = 518.91
= H3+ hh1-3
= 4447 + 744 = 518.91
H2 = 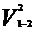 /2g + P2/γ + (Z2 - Z8)
= 236.15
/2g + P2/γ + (Z2 - Z8)
= 236.15
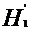 = H2+ hh1-2
= 236.15 + 258.48 = 488.63 m
= H2+ hh1-2
= 236.15 + 258.48 = 488.63 m
H1 = max (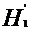 ;
;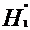 ) = 518.91
) = 518.91
H0
= H1 + hh01
= 518.91 + 327.65 = 846.56m
H0 = 846.56m 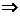 Hapa = H0 ·
Hapa = H0 ·  t
t  a = 846.56·850.5/1000 = 720mcA
a = 846.56·850.5/1000 = 720mcA 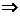 Hapa = 720 mcA
Hapa = 720 mcA
Presiunea la iesirea lichidului din pompa se calculeaza cu
relatia:
pp=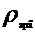 g·Hapa=1000·9.81·720=70.63·106
N/m2
g·Hapa=1000·9.81·720=70.63·106
N/m2
Debitul intrat in rotor este dat de suma debitului din conducta de refulare Q0
si cantitatea de lichid 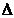 Q pierdut prin neetanseitati:
Q pierdut prin neetanseitati:
Q'= Q0 + 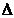 Q = (1.03
Q = (1.03 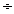 1.1 )· Q0
1.1 )· Q0
Q' = 1.05·33.33·10-3
= 35·10-3 m2/s = 126 m3/h
Consumul de energie pentru invingerea
fortelor de frecare din lagarele pompei, sitemul de etansare al
arborelui la iesirea din carcasa, cuplajul dintre pompa si
motorul de antrenare si cele datorita frecarii arborelui cu mediul
inconjurator este dat de momentul mecanic n
n = p/(p+ 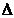 p) + (0.9
p) + (0.9 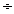 0.93 ) unde p= ·g·Qef·H0
0.93 ) unde p= ·g·Qef·H0
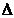 p - puterea consumata pentru
invingerea fortelor de frecare de natura mecanica.Se adopta
p - puterea consumata pentru
invingerea fortelor de frecare de natura mecanica.Se adopta
n
Randamentul
hidraulic este dat de produsul celor trei randamente definite anterior:
p v n m = 0.96·0.84·0.92 = 0.74
Puterea de antrenare a pompei:
Nc =( apa·Q'·Hapa)/75 p [CP]
Nc = (1000·35·10-3·720)/75·0.74
Motorul
de antrenare va fi ales astfel incat puterea lui Nm= Ka·Kc,
unde :
Ka=1.1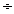 1.2 - coeficient de suprasarcina
1.2 - coeficient de suprasarcina
Nc=1.1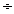 454 = 500 CP=367.7 kW
454 = 500 CP=367.7 kW
Turatia motorului n=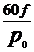 =2950 rot/min unde : f=50 Hz - frecventa
=2950 rot/min unde : f=50 Hz - frecventa
po=1 - numarul perechilor de
poli
Viteza de rotatie a
arboreluu motorului:
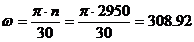 rad/s
rad/s
Turatia specifica si similitudinea
pompelor centrifuge
A. Probleme generale ale similitudinii
Cercetarile se
executa pe modele, care constituie masini sau instalatii ce
indeplinesc conditiile de similitudine, in raport cu prototipul, avand
insa dimensiuni reduse. Pentru transpunerea rezultatelor obtinute pe
modele de prototip, se utilizeaza relatiile de similitudine, bazate
pe analiza fenomenelor fizice din masinile si instalatiile
hidraulice.
Fenomenele fizice care au ca
model matematic comun poarta denumirea de fenomene calitativ identice.
Daca fenomenele au acelasi model matematic se incadreaza in
acelasi domeniu al fizicii, ele constituie o clasa de similitudine,
formata la randul ei din grupuri.
Grupul de similitudine al fenomenelor mecanice presupune o
asemanare geometrica, cinematica si dinamica a
sistemelor componente. Doua sisteme sunt geometrice asemenea daca
1. Fiecarui punct al
unui sistem ii corespunde un punct omolog apartinand celui de-al doilea
sistem
Lungimile omoloage sunt proportionale
3. Unghiurile definite de
lungimi omoloage sunt egale;
In general legea
similitudinii pentru pompele centrifuge se poate defini astfel: daca pompele unei serii functioneaza in acelasi regim
cinematic si dinamic, atunci coeficientul de presiune si randamentul
lor sunt egale.
Forma geometrica a
rotoarelor turbomasinilor in general depinde de 3 parametri
functionali: turatia, debitul si inaltimea de pompare,
adica ea depinde de relatia in care se leaga cei 3 parametri
mentionati pentru a da o marime cu sau fara
dimensiuni.
In cazul pompelor centrifuge si al turbinelor, acest criteriu
de asemanare este turatia specifica sau coeficientul de
rapiditate notat in literatura de specialitate cu "ns". Prin
coeficient de rapiditate al unei pompe se intelege frecventa de
rotatie a pompei model, asemanatoare cu pompa data, avand
acelasi randament care la o inaltime de pompare Hs = 1m
are un debit Qs = 0,075 m3/s si consuma o
putere de Ns = 1CP.
ns=n·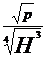 = n·
= n· 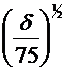 ·
·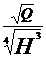 in care :
in care :
n - turatia rotorului [rot/min]
p - puterea pompei exprimata in [CP]
Q - debitul pompei [m3/s]
H - inaltimea de pompare [m]
ns= n· 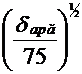
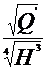
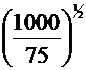
 =15<40
=15<40
ceea ce impune folosirea unei pompe
centrifuge multietajate
ns titei= n· 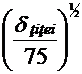
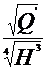
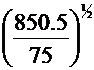
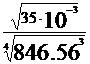 =11,84<40
=11,84<40
Efectul de scara - Pot
apare abateri de la conditiile de formare a grupurilor de similitudine
datorita
rugozitatii
care nu respecta scara geometrica;
nerespectarii conditiilor de
automodelare, adica nerespectarii riguroase a criteriului Reynolds;
neglijarii unor forte care
actioneaza diferit pe model si prototip.
Aceste abateri conduc la modificari
ale randamentelor intre masina prototip si model prin efectul de
scara. In general, randamentul masinii prototip este mai mare ca al
modelului, ceea ce are ca efect acoperitor in acordarea garantiilor.
A.
Criterii
de similitudine
Criteriul
Reynolds - denumit si coeficient de rezistenta (F), este orice complex
adimensional ce contine in structura sa vascozitatea cinematica 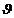 , sau orice combinatie
rezultata intre acest complex adimensional si alti
complecsi adimensionali:
, sau orice combinatie
rezultata intre acest complex adimensional si alti
complecsi adimensionali:
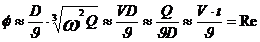
unde 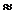 are sensul de identitate
dimensionala.
are sensul de identitate
dimensionala.
Pentru ca fenomenele de la prototip
sa fie identice cu cele de la model, trebuie ca ambele sa aiba
aceeasi cifra Reynolds.
2. Criteriul Fraude - daca dintre
fortele care actioneaza predomina cele masice, si
acest caz are loc la curgerea cu viteze mici, va trebui calculat criteriul
Fraude ce se mai numeste si coeficient de presiune 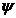
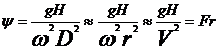 sau
sau
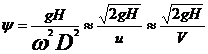
unde V este orice viteza caracteristica in masina hidraulica.
In
consecinta, pentru ca fenomenele de la simil sa fie similare cu
cele de la prototip, in cazul preponderentei fortelor masice trebuie
ca ambele sa aiba aceeasi cifra a lui Fraude.
3. Criteriul Strauhol denumit si
coeficient de debit
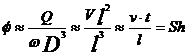
 - viteza unghiulara
- viteza unghiulara
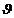 - vascozitatea cinematica
- vascozitatea cinematica
H
- sarcina masinii hidraulice
Q - debitul refulat
V - viteza lichidului
c1 - viteza de propagare a sunetului in lichid
 - densitatea lichidului
- densitatea lichidului
p - presiunea
Criteriul Mach - la viteze extrem de mari, mai
ales la gaze (aer, abur) curgere caracterizandu-se in afara de vitezele "V" si de viteza sunetului "c" va trebui sa se pastreze
constanta cifra lui Mach, denumita si coeficient de elasticitate
(E)
Criteriul Mach se foloseste atunci
cand fortele elastice sunt preponderente
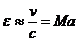
5.
Criteriul Newton - denumit si coeficient de
inertie (i) se foloseste atunci cand preponderente sunt
fortele de inertie si cele exterioare
i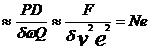
6. Criteriul Euler - denumit si
coeficient de compresibilitate (k) se foloseste atunci cand fortele de presiune sunt preponderente.
7. Randamentul interior ( ) se defineste ca fiind
complexul adimensional obtinut prin combinatia intre puterea
rotorului Pr, presiune si debitul masic.
) se defineste ca fiind
complexul adimensional obtinut prin combinatia intre puterea
rotorului Pr, presiune si debitul masic.
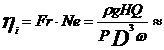
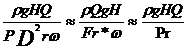
De aici
rezulta ca randamentul interior este produsul criteriilor Fr si
Ne. Daca aceste doua criterii sunt satisfacute,  este un criteriu nedeterminat si deci
este satisfacut in mod implicit.
este un criteriu nedeterminat si deci
este satisfacut in mod implicit.
8.
Coeficientul de rapiditate sau viteza unghiulara specifica (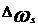 ), ori mai scurt viteza specifica, este un criteriu de similitudine
folosit la clasificarea turbomasinilor.
), ori mai scurt viteza specifica, este un criteriu de similitudine
folosit la clasificarea turbomasinilor.
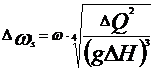 unde
unde
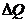 - debitul de lichid
- debitul de lichid
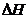 - presiunea hidrostatica
- presiunea hidrostatica
 - viteza unghiulara a arborelui
- viteza unghiulara a arborelui
Pentru
masinile cu mai multe trepte, daca notam cu i numarul treptelor
ce functioneaza in serie si prin j numarul celor care
functioneaza in paralel, atunci
Q = j·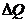 iar H = i·
iar H = i·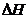
Rotorul dublu se considera ca doi rotori
separati ce lucreaza in paralel.
Viteza
specifica pentru intreaga masina 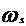
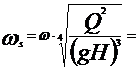
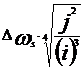
Turatia specifica
ns=n·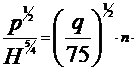
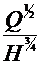 , unde:
, unde:
n
- frecventa rotatiilor in
rot/min
p
- puterea [CP]
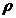 - densitatea fluidului
[kg/m3]
- densitatea fluidului
[kg/m3]
In cazul apei expresia devine: ns=3,65·n·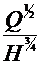
Se mai foloseste de asemenea,
coeficientul dimensional:
nq=n·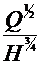
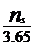
Viteza specifica 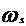 ) prezinta avantaje evidente
fata de turatia specifica (ns), deoarece este
foarte usor de folosit in orice loc si pentru orice lichid, fiind o
marime adimensionala. In literatura de specialitate rotoarele
pompelor centrifuge in functie de turatia specifica sunt
clasificate astfel:
) prezinta avantaje evidente
fata de turatia specifica (ns), deoarece este
foarte usor de folosit in orice loc si pentru orice lichid, fiind o
marime adimensionala. In literatura de specialitate rotoarele
pompelor centrifuge in functie de turatia specifica sunt
clasificate astfel:
ns=40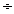
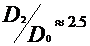 - rotoare radial lente
- rotoare radial lente
ns=80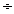
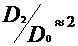 - rotoare radial normale
- rotoare radial normale
ns=150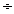 300;
300; 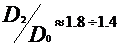 - rotoare rapide
- rotoare rapide
Pentru
o turatie specifica ns=
43.2 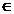 (40;80) vom calcula numarul de trepte necesare (i).
(40;80) vom calcula numarul de trepte necesare (i).
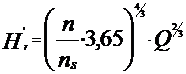
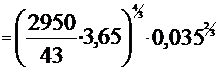
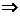
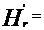 206.4 mcA
206.4 mcA
i=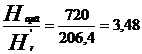
Se adopta I=4 rotoare si vom
recalcula turatia specifica:
Hrapa=  mcA
mcA
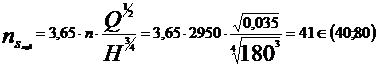
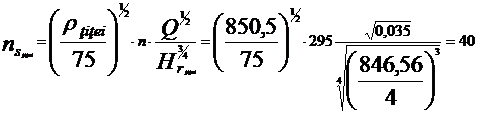
Coeficientul
de rapiditate:
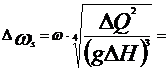
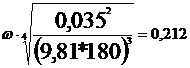
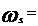
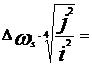
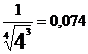



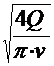
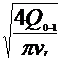
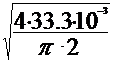
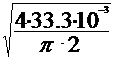
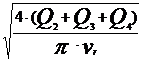
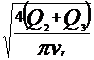
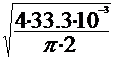

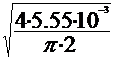
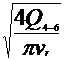
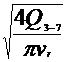
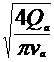
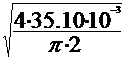
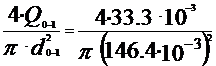 =1.98 m/s
=1.98 m/s =1.94 m/s
=1.94 m/s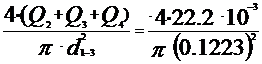 =1.89 m/s
=1.89 m/s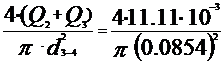 =1.94 m/s
=1.94 m/s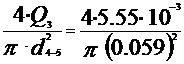 =2.03 m/s
=2.03 m/s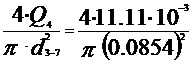 =1.94 m/s
=1.94 m/s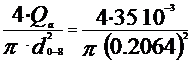 =1.04 m/s
=1.04 m/s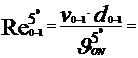 28418,82 < 105
28418,82 < 105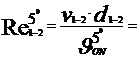 16242.74 < 105
16242.74 < 105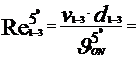 22661.47 < 105
22661.47 < 105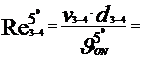 16242.74 < 105
16242.74 < 105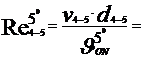 11742.15 < 105
11742.15 < 105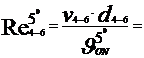 11742.15 < 105
11742.15 < 105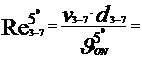 16242.74 < 105
16242.74 < 105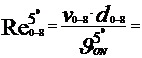 21047 < 105
21047 < 105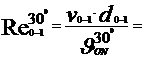 43920.0 < 105
43920.0 < 105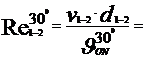 25102.42 < 105
25102.42 < 105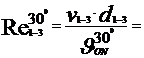 35022.27 < 105
35022.27 < 105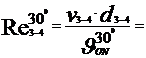 25102.42 < 105
25102.42 < 105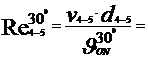 18146.97 < 105
18146.97 < 105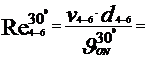 18146.97 < 105
18146.97 < 105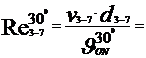 25102.42 < 105
25102.42 < 105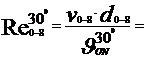 32523.63 < 105
32523.63 < 105
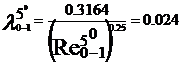
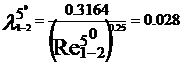
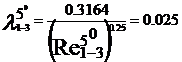
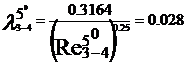

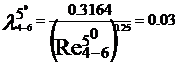
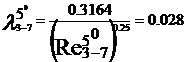
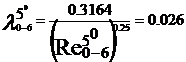
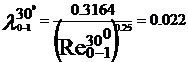
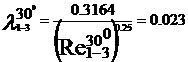
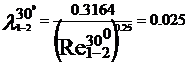

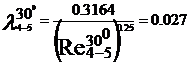
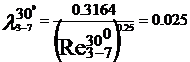
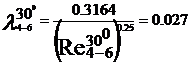
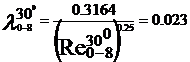

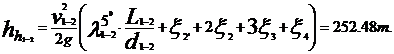
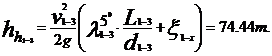
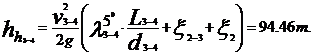
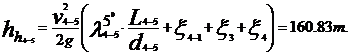
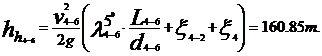
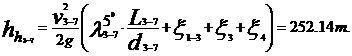

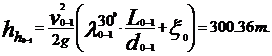
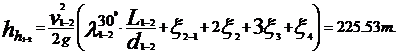
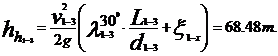
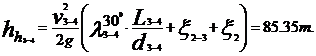
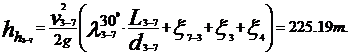
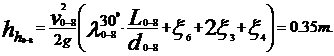
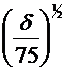 ·
·