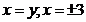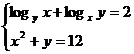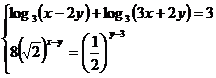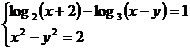Sisteme de ecuatii logaritmice rezolvate
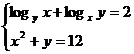
Rezolvare:
Conditiile de existenta ale logaritmului
sunt 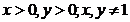
Se noteaza 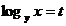 . Prima ecuatie a sistemului devine:
. Prima ecuatie a sistemului devine: 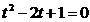 , adica
, adica
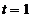 si de aici
si de aici 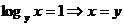 cu aceasta a doua ecuatie a sistemului devine:
cu aceasta a doua ecuatie a sistemului devine:
 cu
radacinile
cu
radacinile  . Retinem
. Retinem 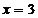 pentru care
pentru care 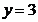 , deci solutiile sistemului
, deci solutiile sistemului 
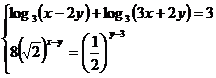
Rezolvare:
Conditiile de existenta ale
logaritmului sunt: 
Ecuatia exponentiala a sistemului este scrisa
sub forma 
Ecuatia logaritmica a sistemului se
mai scrie
 sau
sau  , sistemul devine:
, sistemul devine:

Solutia ce
verifica conditiile puse la inceput este: 
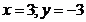
3. 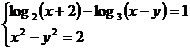
Rezolvare:
Conditiile de existenta ale
logaritmului sunt: 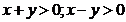
In prima ecuatie se aduc logaritmii in
aceeasi baza (2) si se obtine relatia:


Din a doua ecuatie a sistemului
rezulta  , deci prima
ecuatie a sistemului are forma
, deci prima
ecuatie a sistemului are forma  , iar de aici
, iar de aici 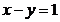 .
.
Sistemul se reduce la rezolvarea sistemului:
 rezulta
rezulta 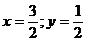

Rezolvare:
Se scrie prima
ecuatie sub forma:  . Se observa ca
. Se observa ca  este strict crescatoare si deci Injectiva.
este strict crescatoare si deci Injectiva.
Din prima
ecuatie  , iar din a doua:
, iar din a doua:  deci solutiile
sistemului sunt:
deci solutiile
sistemului sunt: