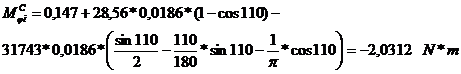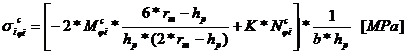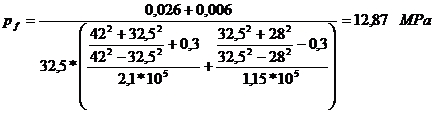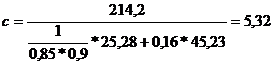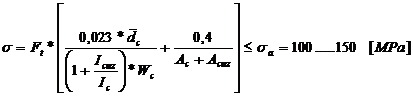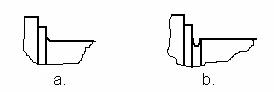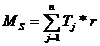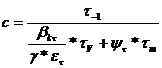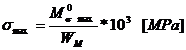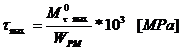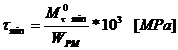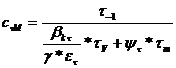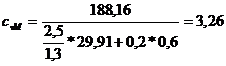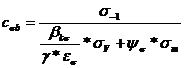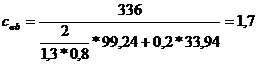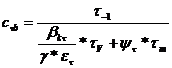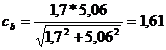AUTOVEHICULE RUTIERE - Calculul si Constructia Motoarelor cu Ardere
Interna - partea 2
IV.†† Biela
Piciorul bielei:
Dimensiunile
caracteristice ale piciorului bielei (Fig. 4.1), se determina pe baza
datelor constructive. Piciorul bielei suporta:
solicitarea de intindere produsa de
forta de inertie a grupului piston;
solicitarea de compresiune produsa de
forta de presiune a gazelor;
solicitarea de fretare, produsa de
bucsa sau de bolt.

Fig.
4.1 Dimensiunile caracteristice piciorului bielei
Semnificatia
punctelor de pe diagrama este:
 - diametrul
exterior al boltului;
- diametrul
exterior al boltului; - diametrul
interior al piciorului;
- diametrul
interior al piciorului;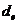 - diametrul
exterior al piciorului;
- diametrul
exterior al piciorului;  - grosimea
radiala a bucsei;
- grosimea
radiala a bucsei; 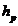 - grosimea
radiala a piciorului;
- grosimea
radiala a piciorului; 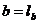 - lungimea de
sprijin al bielei (lungimea bielei).
- lungimea de
sprijin al bielei (lungimea bielei).
In
tabelul de mai jos sunt date urmatoarele date caracteristice ale
piciorului bielei (Tabel 4.1):
Tabel 4.1
|
MAC
|
|
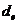
|
(1,3..1,7)*deb
|
|
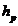
|
(0,16..0,2)*deb
|
|

|
(0,08..0,085)*deb
|



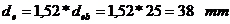


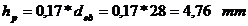

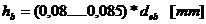

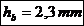

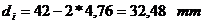
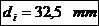
Solicitarea de
intindere:
Forta de tractiune  are valoare
maxima cand forta de presiune este neglijabila, atunci cand
pistonul se afla la pmi la inceputul cursei de admisie.
are valoare
maxima cand forta de presiune este neglijabila, atunci cand
pistonul se afla la pmi la inceputul cursei de admisie.
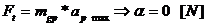

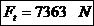
Unghiul de incastrare:

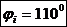
Raza medie a piciorului:

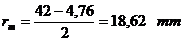
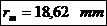
Forta normala si momentul de
incovoiere determinat de forta de tractiune:
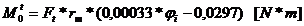
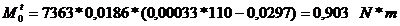




Tensiunile in fibra exterioara, respectiv
interioara pentru sectiunea de incastrare:
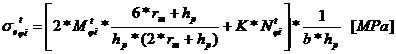
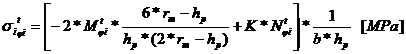

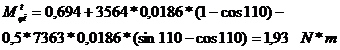


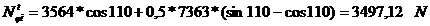
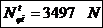
 - factor care pentru
boltul flotant este mai mic ca 1.
- factor care pentru
boltul flotant este mai mic ca 1.
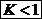

unde:
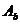 - aria
bucsei;
- aria
bucsei;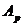 - aria
pistonului;
- aria
pistonului;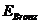 - modulul de
elasticitate pentru bronz;
- modulul de
elasticitate pentru bronz;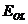 - modulul de
elasticitate pentru otel.
- modulul de
elasticitate pentru otel.

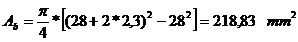
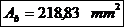
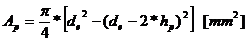
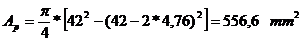
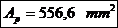
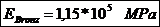
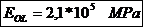
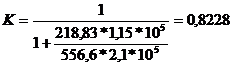
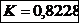
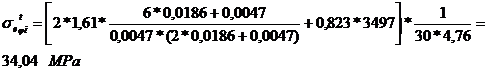
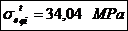
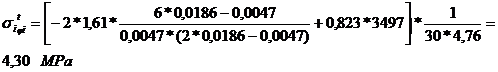
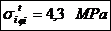
Solicitarea la
compresiune:
Forta
de compresiune 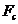 are valoare
maxima atunci cand presiunea din cilindru exte maxima. Se admite
conventional ca forta de presiune se realizeaza la pmi, la
inceputul cursei de destindere si ea este redusa de forta
de inertie a grupului piston.
are valoare
maxima atunci cand presiunea din cilindru exte maxima. Se admite
conventional ca forta de presiune se realizeaza la pmi, la
inceputul cursei de destindere si ea este redusa de forta
de inertie a grupului piston.

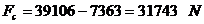

Forta normala si momentul de
incovoiere date de forta de compresiune:
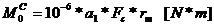

Pentru: 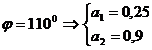 .
.
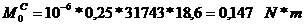

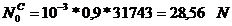

Forta normala si momentul
incovoietor in sectiunea de incastrare date de forta de compresiune:

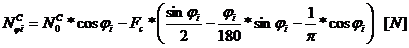
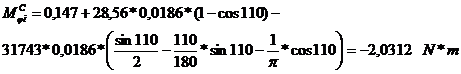
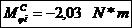
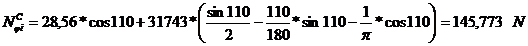

Tensiunea in fibra interioara, respectiv cea
exterioara data de forta de comprimare in sectiunea de
incastrare:

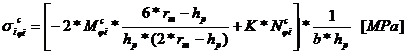
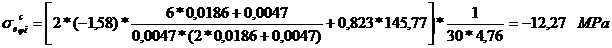
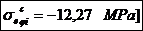
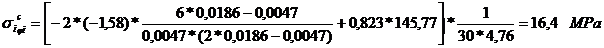
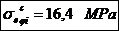
Solicitarea de
fretare:
Aceasta este o solicitare de compresiune. Ansamblul
picior-bucsa se asimileaza cu un sistem de doua tuburi
fretate fabricate din materiale diferite. In timpul functionarii,
bucsa din bronz se dilata mai mult decat piciorul, ceea ce produce o
solicitare suplimentara de compresiune.
Diferenta dintre cresterea diametrului exterior
al bucsei si cel interior al piciorului reprezinta strangerea
termica  la care se adauga
strangerea de montaj
la care se adauga
strangerea de montaj 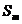 .
.
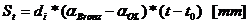
unde:
 -
coeficientul de dilatare termica liniara a bronzului;
-
coeficientul de dilatare termica liniara a bronzului; -
coeficientul de dilatare termica liniara a otelului.
-
coeficientul de dilatare termica liniara a otelului.


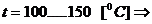
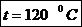
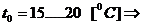
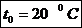

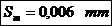
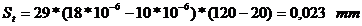
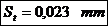
Presiunea de
fretaj:

unde:
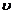 - coeficientul
lui Poisson.
- coeficientul
lui Poisson.

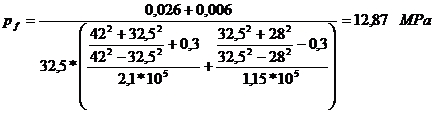
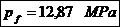
Tensiunea in
fibra exterioara, respectiv cea interioara determinata de
presiunea de fretaj:
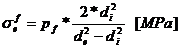
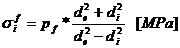

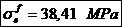

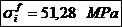
Tensiunea
maxima si minima in fibra exterioara:


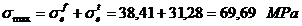

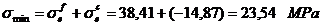
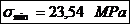
Coeficientul de siguranta:

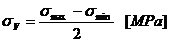
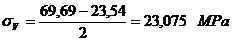

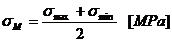


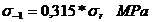
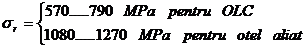
Se adopta:

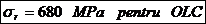

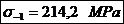

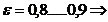


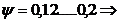
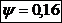



Deformatia
maxima a piciorului:
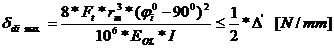
unde:
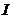 - momentul de
inertie al sectiunii.
- momentul de
inertie al sectiunii.
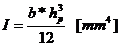
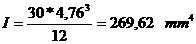
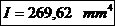
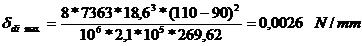
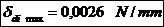
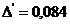
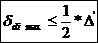
Calculul
corpului bielei:
Dimensiunile
caracteristice se stabilesc deasemenea pe baza datelor statistice. Calculul se
face pentru sectiunea mediana M-M si pentru sectiunea
minima m-m sub picior.
Se
determina mai intai Hp,
apoi se calculeaza a, B, h, e
in sectiunea m-m inlocuind pe H cu Hp Apoi
se calculeaza HC in
zona capului si apoi se determina a, B, h, e in sectiunea d-d. Valorile pentru a, B, h, e se determina facand media aritmetica a
valorilor corespunzatoare din sectiunea m-m, respectiv d-d
()
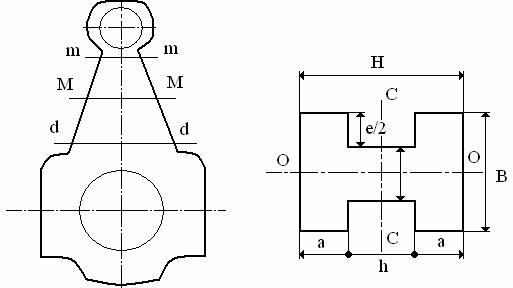
Fig. 4.2 Calculul corpului bielei
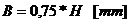
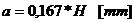


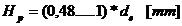

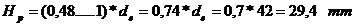


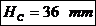
Pentru sectiunea m-m: H se inlocuieste cu Hp:

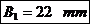



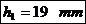


Pentru sectiunea d-d: H se inlocuieste cu HC:

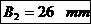



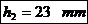
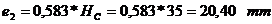

Pentru sectiunea M-M:
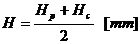
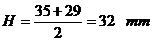
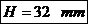
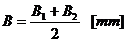


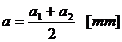
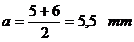
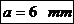
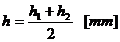

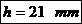

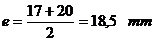

In
sectiunea minima, forta de tractiune:

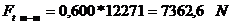

Tensiunea de
intindere:
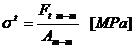
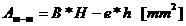
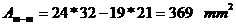


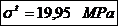
Forta de
compresiune:

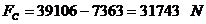
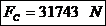
Tensiunea de
compresiune:
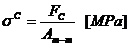


In planul de oscilatie, lungimea de flambaj este egala
cu lungimea bielei.
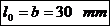
In planul de incastrare:

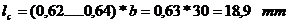

Coeficientul de
corectie in planul de oscilatie:
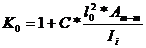

unde:
 - limita de
elasticitate;
- limita de
elasticitate; - momentul de
inetie al sectiuni fata de planul de incastrare C-C.
- momentul de
inetie al sectiuni fata de planul de incastrare C-C.

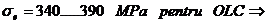




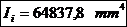
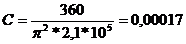

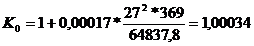

Coeficientul de
corectie in planul de incastrare:

unde:
 - momentul de
inetie al sectiuni fata de planul de incastrare O-O.
- momentul de
inetie al sectiuni fata de planul de incastrare O-O.

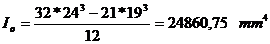

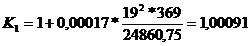

Tensiunea de
compresiune si flambaj in planul de oscilatie:
 oscilatie
oscilatie
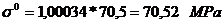

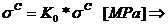 incastrare
incastrare
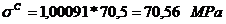

Tensiunea
maxima si minima:
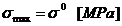



Coeficientul de
siguranta:

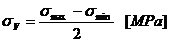


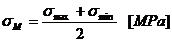

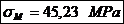
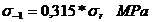
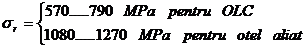
Se adopta:

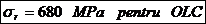

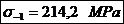

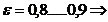


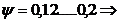
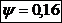
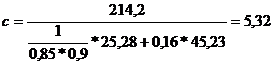
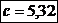
In
sectiunea mediana calculul se face analog cu urmatoarea
precizare:
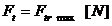
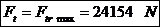
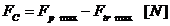

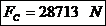
Calculul capului
bielei:
Dimensiunile
principale ale capului bielei sunt determinate de cele ale fusului maneton. In
tabelul de mai jos sunt date dimensiunile fusului maneton si ale cuzinetului
(Tabel 4.2).
Tabel 4.2
Dimensiuni
|
MAC
|
|
in linie
|
in V
|
|
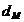
|
(0,55..0,72)*D
|
(0,6..0,72)*D
|
|

|
(0,5..0,65)*
dM
|
(0,8..1)* dM
|
|
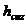
|
0,9..2,5 mm
(0,03..0,05)*dM
|
2..4 mm
|
unde:
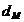 - diametrul
exterior al manetonului;
- diametrul
exterior al manetonului; - lungimea
fusului maneton;
- lungimea
fusului maneton;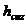 - grosimea
radiala a cuzinetului.
- grosimea
radiala a cuzinetului.
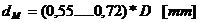

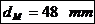


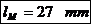


Datorita
racordarii largi a capului cu corpul, solicitarea de compresiune este
neinsemnata. Solicitarea de intindere se transmite numai capacului si
este determinata de forta de inertie a maselor in miscare
de translatie si de forta de inertie a masei bielei
aferenta miscarii de rotatie, mai putin masa
capacului.

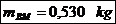
In
figura de mai jos sunt prezentate dimensiunile capacului de biela
(Fig. 4.3):
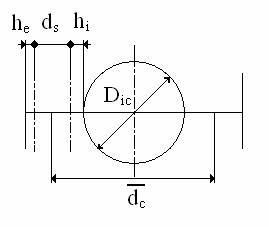
Fig. 4.3 Dimensiunile capacului de biela
unde:
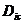 - diametrul
interior al capacului;
- diametrul
interior al capacului;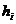 - grosimea
peretelui interior;
- grosimea
peretelui interior; - grosimea peretelui exterior;
- grosimea peretelui exterior; - diametrul mediu
al capului;
- diametrul mediu
al capului; - diametrul
surubului.
- diametrul
surubului.



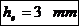

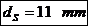

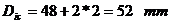
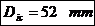
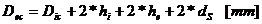
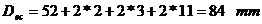
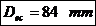
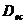 - diametrul exterior
al capacului.
- diametrul exterior
al capacului.
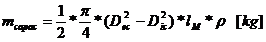
unde:
 - densitatea
materialului.
- densitatea
materialului.

Se alege:

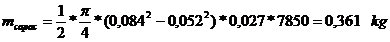

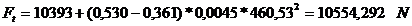


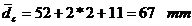
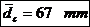
Tensiunea din
fibra exterioara:
Deoarece
unghiul de incastrare variaza in limitele restranse, se determina
tensiunea din fibra exterioara in ipoteza ca unghiul de incastrare
este de 1300.
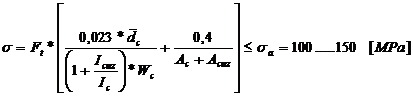
unde:
 - momentul de
inertie al sectiunii cuzinetului;
- momentul de
inertie al sectiunii cuzinetului; - momentul de
inertie al sectiunii capului;
- momentul de
inertie al sectiunii capului; - modulul de
reuzistenta la incovoiere pentru capul bielei;
- modulul de
reuzistenta la incovoiere pentru capul bielei; - aria
sectiunii transversale a capului;
- aria
sectiunii transversale a capului; - aria
sectiunii transversale a cuzinetului.
- aria
sectiunii transversale a cuzinetului.

unde:
 - lungimea
cuzinetului.
- lungimea
cuzinetului.
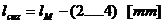





unde:
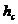 -
inaltimea capacului.
-
inaltimea capacului.




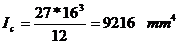
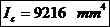






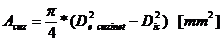

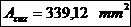





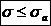
Deformatia
maxima a capului:

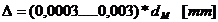
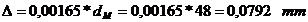




V. Arborele cotit
Arborele
cotit transforma miscarea de translatie a pistonului intr-o
miscare de rotatie si transmite momentul motor dezvoltat prin
arderea combustibilului spre utilizator.
Arborele
cotit este format dintr-un numar de coturi egal cu numarul de cilindri
la motoarele in linie si cu jumatate din numarul de cilindri la
motoarele in V.
De
asemenea trebuie sa aiba cel putin doua fusuri de reazem
numite fusuri paliere. Fiecare cot
este format dintr-un fus maneton (maneton) pe care se articuleaza biela (bielele
in cazul motoarelor in V) si doua brate alaturate acestuia.
Partile
componente ale unui arbore cotit sunt (fig. 5.1):
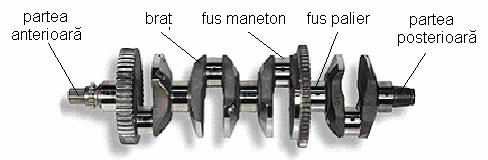
Fig. 5.1 Partile
componente al arborelui cotit
- fusul maneton - pe care se
articuleaza biela;
- fusul palier - reprezinta lagarul
de sprijin al arborelui cotit;
- bratul - face legatura
intre fusul palier si fusul maneton.
In
partea posterioara a motorului se fixeaza volantul si organele
de legatura cu utilizatorul, iar la partea anterioara se
fixeaza elementele necesare pentru antrenarea unor sisteme auxiliare (
sistemul de distributie a gazelor, sistemul de racire, sistemul de
ungere).
Arborele cotit este supus
unor solicitari extrem de mari si, de aceea, este necesar sa
posede o rigiditate deosebita. Acest lucru se poate realiza prin
marirea dimensiunilor constructive, solutie limitata de
scaderea frecventei vibratiilor libere (din cauza cresterii
masei proprii) cu pericolul aparitiei fenomenului de rezonanta
in timpul functionarii.
Pentru a micsora
masa, o solutie posibila este gaurirea fusurilor. Aplicand
aceasta solutie se imbunatateste rezistenta
la oboseala si se ofera posibilitatea de a aduce uleiul de
ungere spre fusuri prin interiorul arborelui cotit. Micsorarea abaterilor
de forma si pozitie are o deosebita importanta
atat in ceea ce priveste fusurile, cat si dispunerea coturilor.
Calitatea suprafetei fusurilor este importanta pentru micsorarea
uzurilor.
Uzual, numarul de
fusuri palier este cu unul mai mare decat numarul de fusuri maneton. La
MAS mai putin solicitate exista posibilitatea ca numarul de
fusuri palier sa fie mai mic decat cel al fusurilor maneton, caz in care
unele brate sunt comune pentru doua fusuri maneton alaturate. La
motoarele moderne bratele au o forma eliptica (fig. 5.2a), care
s-a dovedit avantajoasa in ceea ce priveste rezistenta la
solicitarile mecanice. La motoarele extrem de solicitate bratul poate
ajunge pana la forma circulara (fig. 5.2b).
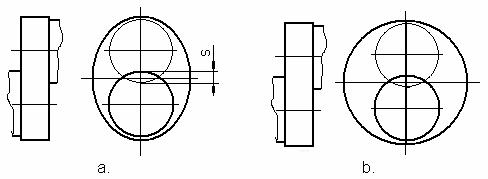
Fig.
5.2 Forme ale bratelor
Prin suprapunerea
fusurilor (fig. 5.2 a) se mareste rezistenta la oboseala a
arborelui. Reducerea concentratorilor de tensiuni in zona de racordare a
fusurilor cu bratul se face prin intermediul unor praguri (fig. 5.3).
Racordarea fusului cu
pragul se face fie cu o raza de racordare (fig. 5.3a), fie cu
degajari (fig. 5.3b).
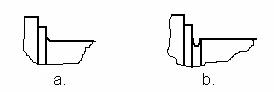
Fig.
5.3 Racordari ale fusului
Arborii cotiti pentru
motoarele care echipeaza autovehicule rutiere pot fi fabricati din
otel sau din fonta. Procedeul de obtinere a semifabrica-tului
pentru arborii din otel este forjarea in matrita, iar arborii
din fonta se realizeaza prin turnare.
Turnarea are avantajul
ca realizeaza mai usor forma contragreutati-lor. La
arborii din otel, contragreutatile se fabrica llegee
si sunt fixate de arbore cu asamblari filetate.
Calculul
arborelui cotit:
Arborele se dimensioneaza
pe baza datelor statistice. Calculul are un caracter de verificare a acestor
dimensiuni.
Fusurile
fiind supuse frecarii si uzarii, se verifica la presiune de
contact si la incalzire. Coturi arborelui sunt supuse la solicitarea
de incovoiere si de torsiune. Verificarea la vibratii torsionale
urmareste determinarea turatiilor critice si a tensiunilor
care apar la rezonanta.
In
tabelul de mai jos sunt date dimensiunile arborelui (Tabel 5.1):
Tabel 5.1
|
in linie
|
|
MAC
|
|
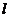
|
(1,15..1,35)*D
|
|
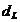
|
(0,7..0,85)*D
|
|

fus
intermediar
fus de
capat
|
(0,45..0,6)*dL
(0,55..0,75)*dL
|
|
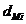
|
(0,6..0,75)*dM
|
|

|
(1,5..2)*dM
|
|

|
(0,2..0,35)*dM
|
|

|
(0,07..0,1)*dM
|
Dimensiunile
caracteristice ale arborelui cotit sunt prezentate in figura de mai jos (Fig.
5.4):

Fig. 5.4 Dimensiunile caracteristice ale arborelui
cotit
unde:
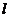 - lungimea
cotului;
- lungimea
cotului;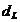 diametrul fusului palier;
diametrul fusului palier;
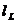 - lungimea
fusului palier;
- lungimea
fusului palier;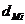 - diametrul
interior al fusului maneton;
- diametrul
interior al fusului maneton; -
latimea bratelor;
-
latimea bratelor; - grosimea
bratelor;
- grosimea
bratelor; - raza de
racordare dintre fus si brat;
- raza de
racordare dintre fus si brat;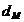 - diametrul
fusului maneton;
- diametrul
fusului maneton; - lungimea
fusului maneton;
- lungimea
fusului maneton; - diametrul
interior al fusului palier.
- diametrul
interior al fusului palier.
Diametrul fusului
palier:
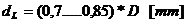

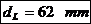
Lungimea fusului
maneton:
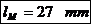
Lungimea fusului
palier:




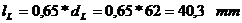
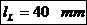
Diametrul
fusului maneton:
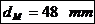
Diametrul
interioral fusului maneton:
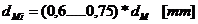


Diametrul
interior al fusului palier:

Latimea
bratelor:

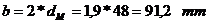
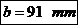
Grosimea
bratelor:

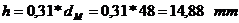

Raza de
racordare dintre fus si brat:
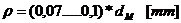

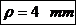
Lungimea
cotului:
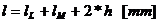 sau
sau 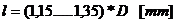
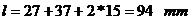 sau
sau 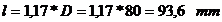
 sau
sau
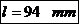
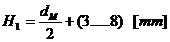

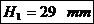



Verificarea fusului la presiunea de
contact si incalzire:
Presiunile specifice pe fusul maneton:
Presiunea specifica
medie:


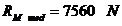

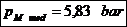
Presiunea
specifica maxima:
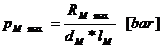
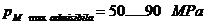


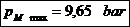
5.1.2.2. Presiunile specifice pe fusul palier:
Presiunea
specifica medie:
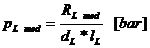

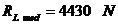
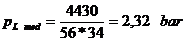

5.1.2.2.2. Presiunea specifica maxima:
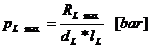


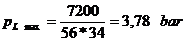
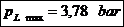
Verificarea
fusului la incalzire:
Coeficientul
de uzura pentru fusul maneton:

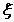 - tine cont
de oscilatiile bielei si are valori intre
- tine cont
de oscilatiile bielei si are valori intre 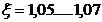 .
.
Se alege: 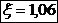

Se adopta:  .
.


Coeficientul
de uzura pentru fusul palier:

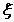 - tine cont
de oscilatiile bielei si are valori intre
- tine cont
de oscilatiile bielei si are valori intre 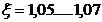 .
.
Se alege: 

Se adopta:  .
.


Diagramele
polare:
Diagrama polara a fusului maneton:
Solicitarea pe fusul maneton rezulta din compunerea
vectoriala dintre forta de inertie a masei bielei aferenta
miscarii de rotatie  si forta in
lungul bielei
si forta in
lungul bielei 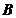 .
.

Fig. 5.5 Constructia diagramei
Diagrama polara este o constructie grafica
care permite compunerea vectoriala a fortelor 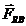 si
si 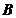 pentru diferite
pozitii ale mecanismului biela-manivela precizate de unghiul
pentru diferite
pozitii ale mecanismului biela-manivela precizate de unghiul  . In general diagramele polare se construiesc pentru valori
ale unghiului
. In general diagramele polare se construiesc pentru valori
ale unghiului  din 300 in
300. In timpul functionarii, fusul maneton se roteste
pe suprafata interioara a capului bielei.
din 300 in
300. In timpul functionarii, fusul maneton se roteste
pe suprafata interioara a capului bielei.
Pentru constructia diagramei polare a fusului
maneton se considera ca manivela este fixa si se biela se
roteste in jurul axei fusului maneton. La o scara aleasa a
lungimilor se construieste un cerc cu centrul in punctul M, a carui
raza este egala cu lungimea bielei.
La aceeasi scara a lungimilor, pe diametrul
vertical al cercului cu centrul in punctul M, se precizeaza punctul O
situat sub punctul M, astfel incat segmentul MO=r, raza manivelei. Cu centrul
in O se traseaza un cerc de raza oarecare care nu intersecteaza
nici un punct cercul cu centrul in M, dar intersecteaza diametrul
orizontal al acestuia care trece prin punctul M in doua puncte. Cercul cu
centrul in O se imparte in 12 parti egale (Fig. 5.6).

Fig.
5.6 Impartirea cercului
Prelungirea diagramelor
trasate in cercul cu centrul in O, intersecteaza cercul cu centrul in
punctul M in punctul Pi. OMPi
reprezinta pozitia mecanismului biela-manivela pentru
variatii ale unghiului  de 300
(Fig. 5.7).
de 300
(Fig. 5.7).

Fig.
5.7 Pozitia mecanismului biela-manivela
Cu varful in M se
traseaza la o scara aleasa a fortelor, vectorul 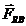 astfel incat punctul
sau de aplicatie sa fie in OM (Fig. 5.8).
astfel incat punctul
sau de aplicatie sa fie in OM (Fig. 5.8).

Fig.
5.8 Constructia vectorului 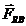
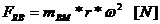

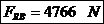
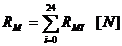
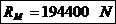

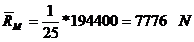
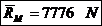
In tabelul de mai jos sunt date valorile pentru fusul
maneton
(Tabel 5.2).
Tabel 5.2
|
alfa
|
Numar
|
B
|
RM
|
|
[grd]
|
criteriu
|
[N]
|
[N]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Diagrama polara a fusului palier:
Solicitarea produsa asupra unui fus palier este suma
vectoriala a jumatatilor rezultantelor  care
actioneaza pe fusurile paliere invecinate (Fig. 5.9). Cu observatia
ca in locul fortei
care
actioneaza pe fusurile paliere invecinate (Fig. 5.9). Cu observatia
ca in locul fortei 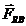 apare forta
apare forta  .
.



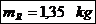
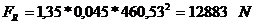
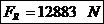

Fig. 5.9 Solicitarile pe fusul palier
Pe diagrama polara a fusului maneton la scara
fortelor aleasa anterior se traseaza segmentul MOL=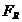
Se fac doua asemenea diagrame polare cu centrul OM precizat, se suprapun cele
doua astfel incat punctul OL sa coincida si se
rotesc intre ele astfel incat unghiul format de axele care includ segmentul OM
sa fie egal cu unghiul dintre manivela. La insumarea vectoriala,
trebuie luat in considerare si defazajul dintre aprinderi.
In tabelul de mai jos sunt date valorile pentru fusul
palier
(Tabel 5.3).
Tabel 5.3
|
alfa
|
Numar
|
B
|
RM
|
RL1
|
RL2
|
|
[grd]
|
criteriu
|
[N]
|
[N]
|
[N]
|
[N]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Verificarea la
oboseala:
Fusurile paliere sunt solicitate la torsiune de un ciclu
asimetric. Fusurile paliere dinspre partea centrala (ventilator) sunt
solicitate de momente de torsiune medii, mai mici decat cele dinspre partea
posterioara si in special fusul palier cate insumeaza momentele
produse de cilindrii anteriori (Fig. 5.10).
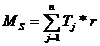

unde:
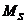 - momentul de intrare;
- momentul de intrare;
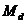 - momentul de
iesire.
- momentul de
iesire.
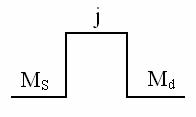
Fig. 5.10 Momentelede intrare si de iesire
la arbore
La calculul arborelui cotit numerotarea cilindrilor se
inverseaza, cilindrul 1 va fi dinspre ventilator (Fig. 5.11).
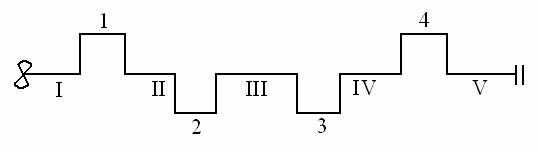
Fig. 5.11 Numerotarea arborelui cotit

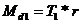 - coloana din tabelul
de momente corespunzatoare lui M4.
- coloana din tabelul
de momente corespunzatoare lui M4.

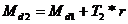 - coloana M4
+ coloana M3.
- coloana M4
+ coloana M3.
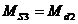
In tabelul de mai jos sunt date valorile calculate (Tabel
5.4):
Tabel 5.4
|
alfa
|
Ms1
|
Ms2
|
Ms3
|
|
alfa
|
Md1
|
Md2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tensiunile
maxime si minime:
Tensiunea
maxima:
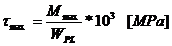
 - modulul de
rezistenta polar al fusului palier.
- modulul de
rezistenta polar al fusului palier.
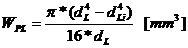
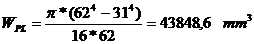

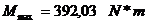
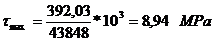
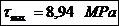
Tensiunea
minima:

 - modulul de
rezistenta polar al fusului palier.
- modulul de
rezistenta polar al fusului palier.
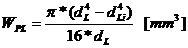



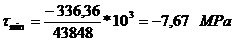
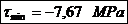
Coeficientul de
siguranta la oboseala:
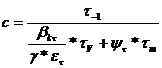
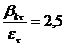
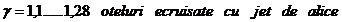

Rezistenta la oboseala:
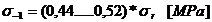
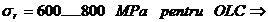




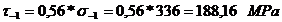
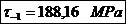
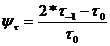
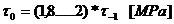
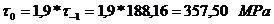

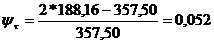
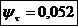
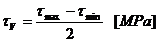
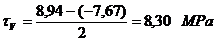
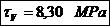
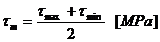

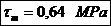

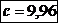
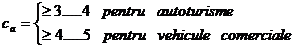
Calculul fusului
maneton:
Fusul maneton este supus la incovoiere si torsiune.
Modelul de calcul este valabil pentru un cot care este sprijinit pe 2 reazeme
si este incarcat cu forte concentrate cunoscute.
Reactiunile din reazeme se determina din
ecuatiile de echilibru ale fortelor si momentelor. Fortele
care actioneaza asupra fusului maneton se descompun dupa
doua directii: una normala situata in planul cotului,
cealalta tangenta la fusul maneton (Fig. 5.12).
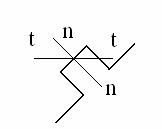
Fig. 5.12 Fortele care actioneaza pe
fusul maneton
Forta
tangentiala la fusul maneton:
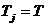 †- din tabelul de
forte.
†- din tabelul de
forte.

unde:
 †- componenta
radiala a fortei in lungul bielei;
†- componenta
radiala a fortei in lungul bielei;
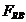 †- forta de
inetie a masei bielei aferenta miscarii de rotatie;
†- forta de
inetie a masei bielei aferenta miscarii de rotatie;
 †- forta de
inetie a masei fusului manetonului aferenta miscarii de
rotatie.
†- forta de
inetie a masei fusului manetonului aferenta miscarii de
rotatie.
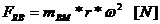


unde:
 - masa fusului
maneton.
- masa fusului
maneton.

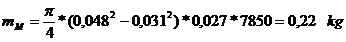
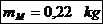

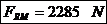
Reactiunile
din reazemul stang:


unde:
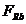 †- forta de
inertie determinate de masele neechilibrate;
†- forta de
inertie determinate de masele neechilibrate;
 †- forta de
inertie a contragreutatilor.
†- forta de
inertie a contragreutatilor.
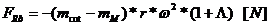

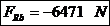

Momentul
incovoietor in planul tangential:
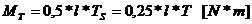
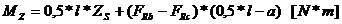
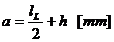


Momentul de
incovoiere in sectiunea slabita:



Momentul de torsiune al manetonului:

Toate
aceste calcule se organizeaza intr-un tabel in care apare:  .
.
In
tabelul de mai jos sunt rezultatele formulelor scrise la punctele 5.1.7; 5.1.8; 5.1.9; 5.1.10; 5.1.11
(Tabel 5.5).
Tabel 5.5
|
alfa
|
T
|
ZB
|
Zj
|
Zs
|
MT
|
MZ
|
Mσ
|
Mζ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Solicitarea de incovoiere:
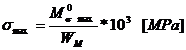
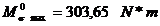

unde:
 - modulul de
rezistenta al fusului maneton.
- modulul de
rezistenta al fusului maneton.

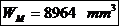
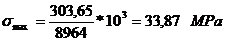
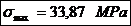

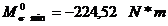
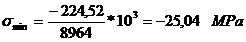

Coeficientul de siguranta la
maneton:


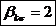


Rezistenta la oboseala:
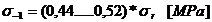
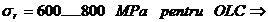



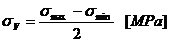
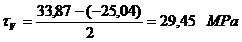
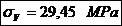
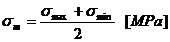
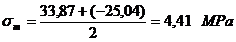



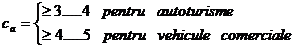
Solicitarea de torsiune:
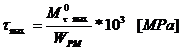


unde:
 - modulul polar de
rezistenta al fusului maneton.
- modulul polar de
rezistenta al fusului maneton.
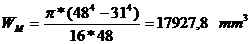
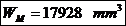

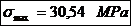
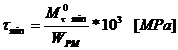

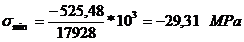
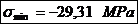
Coeficientul de siguranta pentru fusul
maneton:
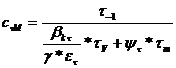
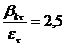
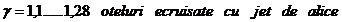
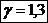
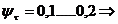
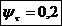
Rezistenta la oboseala:
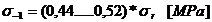
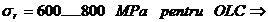




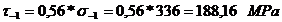
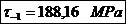
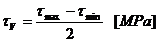
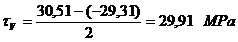

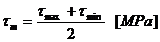
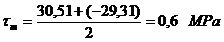

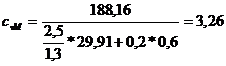

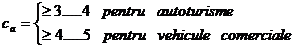
Coeficientul global de siguranta pentru
fusul maneton:
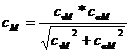
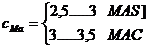
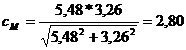
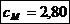
Calculul
bratelor:
Bratul
este solicitat la incovoiere, la intindere, la compresiune si la torsiune.
Incovoierea se face in doua planuri:
planul cotului;
intr-un plan
normal in planul cotului.
Drept
sectiune de calcul se alege ABCD tangente la fusul palier. Punctul cel mai
solicitat este punctul x situat la inetrsectia planului ABCD cu muchia
superioara a fusului palier (Fig. 5.13).
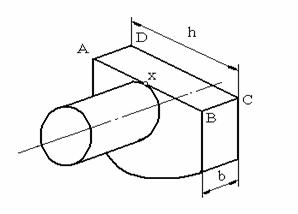
Fig. 5.13 Verificarea bratului la
oboseala
Momentul
incovoietor in planul bratelor:

Momentul
incovoietor in planul normal:

Tensiunea
normala de incovoiere si compresiune:

unde:
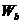 †- modulul de
rezistenta al bratului;
†- modulul de
rezistenta al bratului;
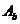 †- aria sectiunii
transversale ale bratului.
†- aria sectiunii
transversale ale bratului.
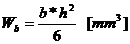
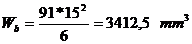

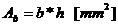


Toate
aceste formule se introduc in tabelul de mai jos (Tabel 5.6).
Tabel 5.6
Tensiunile normale de incovoiere
maxima si minima:


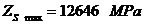
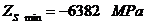
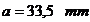

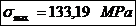

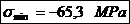
Coeficientul de
siguranta la solicitarea de incovoiere-compresiune pentru brat:
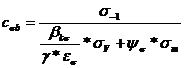

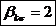
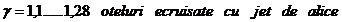
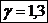
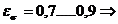

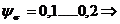

Rezistenta la oboseala:
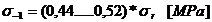
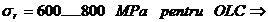



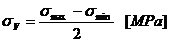
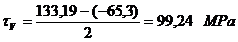
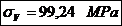
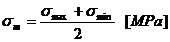

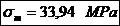
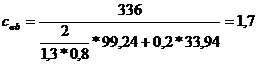

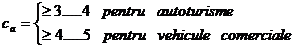
Solicitarea de
torsiune:
Momentul de torsiune al bratului este dat in
Tabelul 5.6 .
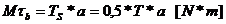
Tensiunea tangentiala
minima si maxima in punctul x:


unde:
 †- coeficientul lui
Saint-Vennant.
†- coeficientul lui
Saint-Vennant.
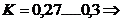



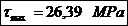
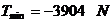
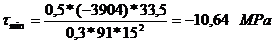
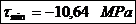
Coeficientul de
siguranta la torsiune pentru brat:
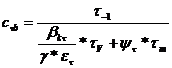
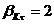
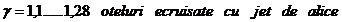
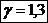
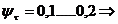
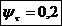
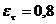
Rezistenta la oboseala:
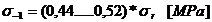
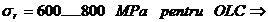




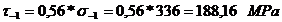
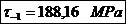
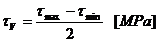
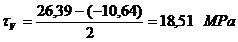

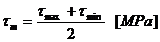
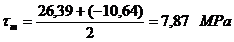
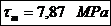

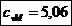
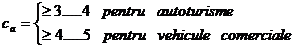
Coeficientul
global de siguranta al bratului:


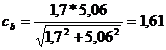
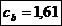
Bibliografie
v
Grunwald
Berthold: "Teoria, calculul si
constructia motoarelor pentru autovehicule rutiere", Editura
Didactica si Pedagogica, Bucuresti, 1980.
v
Gheorghe Bobescu
si altii: "Motoare pentru
automobile si tractoare. Volumul II", Editura Tehnica,
Chisinau, 1998.
v
D.
Abaitancei si altii: "Motoare pentru automobile si tractoare. Constructie si
tehnologie. Volumul I", Editura tehnica, Bucuresti, 1978.
v
R.
Mardarescu si altii: "Motoare pentru automobile si tractoare", Editura Didactica
si Pedagogica, Bucuresti, 1968.



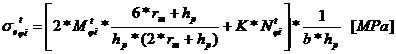
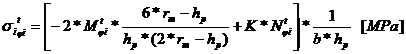
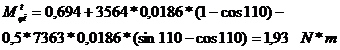

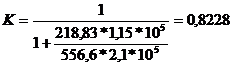
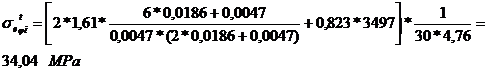
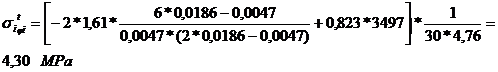
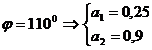 .
.