PROIECT DE LECTIE
Data: 20. IV. 2010
Clasa: a VIII-a A
Scoala: Gimnaziul de Stat "Octavian Goga"
Sighisoara
Titlul lectiei Functii
Scopul lectiei: Recapitularea cunostintelor si
pregatirea atat pentru lucrarea scrisa semestriala pe semestrul
al II-lea, cat si pentru testarea nationala pentru elevii alasei
a VIII-a in anul scolar 2009-2010
Obiectivul general
Dezvoltarea capacitatii de explorare/investigare si rezolvare de
probleme
Obiective operationale: La sfarsitul lectiei, elevul va fi capabil:
sa determine
coordonatele unui punct de pe graficul unei functii;
sa
determine coordonatele punctului de intersectie a graficelor a doua
functii;
sa
reprezinte grafic o functie;
sa
determine sume sau produse care se calculeaza cu ajutorul functiilor;
sa
determine unghiul format de graficul unei functii cu una dintre axele de
coordonate;
sa
aplice formulele functiilor trigonometrice (sinus, cosinus, tangenta,
cotangenta) in contexte variate;
sa
determine aria suprafetei
cuprinsa intre graficul unei functii si axele de coordonate.
Metode
si procedee didactice:
explicatia, exercitiul
Mijloace de invatamant: tabla, creta, creta colorata, culegere de probleme
pentru clasa a VIII-a, fisa de lucru
Tipul lectiei: Fixare si dezvoltare de priceperi si
deprinderi
Timp alocat: 50 minute
DESFǍSURAREA LECTIEI
Momentul organizatoric:
Se face prezenta.
Se stabileste linistea
si atmosfera propice invatarii.
Captarea atentiei si trezirea interesului
elevilor:
Se
reaminteste ca in ora precedenta de matematica s-au
recapitulat regula de 3 simpla si probabilitatile necesare
atat pentru lucrarea scrisa semestriala pe semestrul al II-lea, cat
si pentru testarea nationala.
Revitalizarea cunostintelor:
Se
verifica tema de casa.
Se
verifica, prin intrebari adresate elevilor, daca sunt cunoscute notiunile
de probabilitate, functie, graficul unei functii, distanta
dintre doua puncte, aria unui triunghi.
Anuntarea titlului si a obiectivelor
lectiei:
Se anunta ca
se vor rezolva in continuare exercitii cu functii, din modelele de teste din culegerea de clasa a
VIII -a, ca pregatire pentru testarea nationala.
Fixarea cunostintelor:
Culegere
Testare Nationala, Testul 23, pag. 55, III 1
Se considera punctele A(2; - 3), B(-1; 3) si C(m - 1; 5), m 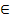 R.
R.
a)
Determinati functia care are drept grafic dreapta
AB.
b)
Determinati numarul real m, astfel incat
punctele A, B si C sa fie coliniare.
Rezolvare:
a)
Fie
functia f : R→R, f(x) = ax + b
A(2; -3) 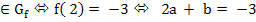
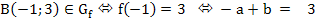

3a / = - 6 a = - 2
-a + b = 3 b = 3 + a b = 3 + ( -2 ) b = 1
Prin urmare, functia f
devine f(x) = -2x + 1.
b)
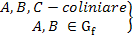 C(m - 1; 5)
C(m - 1; 5) 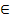

f(m - 1) = 5
-2(m - 1) + 1 = 5
-2m + 2 +1 = 5
-2m = 5 - 3
-2m = 2
m = -1 C( -2; 5)
Obs Orice alta
varianta de rezolvare corecta, este admisa.
Culegere
Testare Nationala, Testul 30, pag. 68, II 3
Fie functiile f : R→R, f(x) = 5 - 3x si g : R→R,
g(x )= 2x - 5.
a)
Aflati cosinusul unghiului ascutit determinat
de axa absciselor si graficul functiei f.
b)
Determinati punctul de intersectie al
graficelor celor doua functii.
Rezolvare:
a)
f(0) = 5 -
3∑0 = 5 ⇨ A (0; 5)
f(1) = 5 - 3∑1 = 2 ⇨ B (1; 2)
g(0) = 2∑0- 5 = -5 ⇨
C (0; -5)
g(1) = 2∑1- 3 = -1 ⇨
D (1; -1)
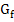 ∩ Ox y = 0 f(x) = 0 5 - 3x = 0 3x = 5 x =
∩ Ox y = 0 f(x) = 0 5 - 3x = 0 3x = 5 x =  E
E
AE = 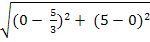 =
=  =
= 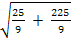 =
= 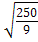 =
= 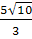
Fie O(0; 0).
EO = 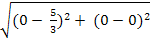 =
= 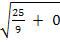 =
= 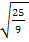 =
= 
cos = cos (
= cos (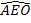
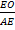 =
=  = =
= =  ∑
∑ 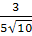 =
= 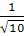 =
= 
b)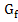 ∩
∩ = M(x; y)
= M(x; y) 
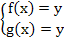

5 - 3x = 2x - 5 - 2x - 3x = -5 - 5 - 5x = -10 x = - 10 : (-5) x = 2
y = 5 -
3∑2 y = 5 - 6 y = - 1
Prin urmare, punctul
de intersectie al graficelor celor doua functii este M(2; -1)
Obs Orice alta
varianta de rezolvare corecta, este admisa.
Culegere
Testare Nationala, Testul 2(Tema), pag. 93, II 3
Se da functia f : R→R, f(x) = 2x - 2.
a)
Trasati graficul functiei f.
b)
Aflati aria triunghiului determinat de graficul
functiei f cu axele de coordonate.
Rezolvare:
a)
f(0) = 2∑0
- 2 = -2 ⇨ A (0; -2)
f(1) = 2∑1 - 2 = 0 ⇨ B (1; 0)
b)
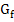 ∩ Ox y = 0 f(x) = 0 2x - 2 = 0 2x = 2 x = 1 ⇨ B (1; 0)
∩ Ox y = 0 f(x) = 0 2x - 2 = 0 2x = 2 x = 1 ⇨ B (1; 0)
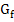 ∩ Oy x = 0 f(0) = -2 ⇨ A (0;
-2)
∩ Oy x = 0 f(0) = -2 ⇨ A (0;
-2)
Deducem deci ca trebuie
sa determinam aria  AOB.
AOB.
 AOB - dreptunghic AAOB
AOB - dreptunghic AAOB  AAOB
AAOB  AAOB
AAOB
Obs Orice alta
varianta de rezolvare corecta, este admisa.
Culegere
Testare Nationala, Testul 26, pag. 61, II 4
Se considera functia f : R→R, f(x) = 3x + 1. Sa se determine abscisa punctului de pe
graficul functiei care are ordonata 6.
Rezolvare:
M(x; 6) 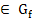 f(x) = 6 3x + 1 = 6 3x = 6 - 1 3x = 5 x =
f(x) = 6 3x + 1 = 6 3x = 6 - 1 3x = 5 x = 
Prin urmare, punctul de pe graficul functiei care
are ordonata 6 este M( ; 6) .
; 6) .
Obs Orice alta
varianta de rezolvare corecta, este admisa.
Culegere
Testare Nationala, Testul 33, pag. 74, II 3
Fie f : R→R, f(x) = ax + b, unde a si b sunt numere
reale.
a)
Aratati ca f(1)+ f(4 )= f(2) + f(3).
b)
Pentru a = 2 si b = -1, reprezentati grafic
functia f.
Rezolvare:
a)
f : R→R, f(x) = ax + b, unde a, b 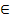 R
R
f(1) + f(4) = f(2) + f(3) a + b + 4a + b =
2a + b + 3a + b
5a + 2b = 5a + 2b†††
(Adevarat), oricare ar fi a,
b 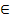 R .
R .
b)
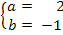 f(x) = 2x - 1
f(x) = 2x - 1
f(0) = 2∑0 - 1 = - 1 ⇨ A (0;
-1)
f(1) = 2∑1 - 1 = 1 ⇨ B (1;
1)
Obs: Orice alta varianta de rezolvare corecta, este
admisa.
Culegere
Testare Nationala, Testul 34, pag. 76, II 4
Se da functia f : R→R, f(x) = -4x + 12.
a)
Aflati punctul de pe grafic care are coordonatele
egale.
b)
Calculati produsul P = f(0) ∑ f(1) ∑ ∑ f(2010).
Rezolvare:
a)
A(x; x) 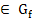 f(x) = x - 4x + 12 = x - 4x - x = -12 -5x = - 12 x =
f(x) = x - 4x + 12 = x - 4x - x = -12 -5x = - 12 x = 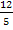 A (
A (
b)
f(0) = -4 ∑ 0 + 12 = 12
f(1) = -4 ∑ 1 + 12
= 8
f(2) = -4 ∑ 2 + 12
= 4
f(3) = -4 ∑ 3 +
12 = 0
f(2010) = -4 ∑
2010 + 12 = - 8028
P = f(0) ∑ f(1) ∑ ∑ f(2010) = 12 ∑ 8 ∑ 4 ∑ 0 ∑ ∑
(- 8028) = 0 .
Obs Orice alta
varianta de rezolvare corecta, este admisa.
Tema pentru acasa:
De recapitulat formulele de calcul prescurtat
si metodele de descompunere in factori.
Culegere
Testare Nationala, Testul 31,††
pag. 71, II 3
Testul 32, pag. 72, II 3
Testul 35, pag. 79, II 4
Fisa
de lucru : exercitiile 1, 2, 3 si 4.

