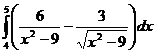Plan de lectie
Data: ..
Clasa a XII-a
Profesor: ..
Tema
lectiei: Integrala definita a
unei functii continue
Tipul lectiei: Lectie de
dobandire de noi cunostinte
Competente generale:
Identificarea
unor date si relatii matematice si corelarea lor in functie
de contextul in care au fost definite.
Prelucrarean
datelor de tip cantitativ, calitativ, structural, contextual cuprinse in
enunturile matematice.
Utilizarea
algoritmilor si conceptelor matematice pentru caracterizarea locala
sau globala a unei situatii concrete.
Exprimarea
caracteristicilor matematice cantitative sau calitative ale unei situatii
concrete si a algoritmilor de prelucrare a acestora.
Analiza
si interpretarea caracteristicilor matematice ale unei situatii -
problema.
Modelarea
matematica a unor contexte problematice variate, prin integrarea
cunostintelor din diferite domenii.
Competente specifice vizate:
C. 3. Utilizarea algoritmilor pentru calcularea unor integrale
definite.
C. 4. Explicarea optiunilor de calcul al integralelor definite, in scopul
optimizarii solutiilor.
C. 6. Aplicarea calculului diferential sau
integral in probleme practice.
Valori si atitudini:
Dezvoltarea unei gandiri deschise,
creative, a independentei in gandire si actiune.
Manifestarea initiativei, a
disponibilitatii de a aborda sarcini variate, a
tenacitatii, a perseverentei si a capacitatii de
concentrare.
Dezvoltarea simtului estetic si
critic, a capacitatii de a aprecia rigoarea, ordinea si
eleganta in arhitectura rezolvarii unei probleme sau a construirii
unei teorii.
Formarea obisnuintei de a
recurge la concepte si metode matematice in abordarea unor situatii
cotidiene sau pentru rezolvarea unor probleme practice.
Formarea
motivatiei pentru studierea matematicii ca domeniu relevant pentru
viata sociala si profesionala.
Desfasurarea lectiei
|
Etapele lectiei
|
Continutul
lectiei
|
Strategii didactice
|
|
1. Moment
organizatoric
|
Asigurarea conditiilor optime pentru desfasurarea
lectiei (curatenie, lumina, tinuta . ).
Verificarea prezentei elevilor.
|
Conversatie
|
|
2. Captarea
atentiei
|
Verificarea frontala a temei, calitativ si cantitativ (prin
sondaj).
|
Conversatie
|
|
3.
Anuntarea temei si a obiectivelor
|
Ne propunem
sa discutam despre
Integrala definita a unei functii continue
|
Conversatie
|
|
4. Reactualizarea cunostintelor
|
Fie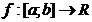 o functie continua pe intervalul o functie continua pe intervalul 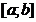 si si  doua primitive ale lui f pe doua primitive ale lui f pe 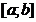 .
Notam .
Notam 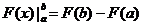 . Deoarece . Deoarece 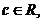 avem avem 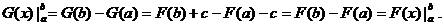
|
Conversatie
|
|
5. Prezentarea
continutului si dirijarea invatarii
|
Definitie. Fie I
un interval si doua numere  . Fie . Fie 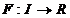 o primitiva a
functiei continue o primitiva a
functiei continue  . Se numeste integrala definita (sau
integrala) a functiei f
de la a la b numarul real notat prin realtia: . Se numeste integrala definita (sau
integrala) a functiei f
de la a la b numarul real notat prin realtia:  (formula lui Leibniz
-Newton ). (formula lui Leibniz
-Newton ).
Observatii:
Variabila de integrare nu joaca
nici un rol in definitia integralei :  . .


 este o
primitiva a lui f care se
anuleaza in t=a. este o
primitiva a lui f care se
anuleaza in t=a.
Exemplu: 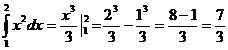
Teorema. Fie functiile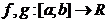 continue pe continue pe 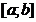 si fie si fie  . Atunci
avem: . Atunci
avem:
a)
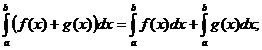
b)

Exemple: Sa se determine :



 . .
|
Conversatie
Explicatie
|
|
6.
Intensificarea retentiei si asigurarea transferului
|
Fisa de lucru exercitiile
de la 1 la 20
|
Conversatie
Explicatie
|
|
7. Asigurarea
feed - back-ului
|
Fisa de lucru exercitiile de la 21 la 25
|
Munca independenta
|
|
8. Evaluare
|
Profesorul rezolva la tabla exercitiile dificile.
Aprecierea elevilor care s-au remarcat la lectie (+, - eventual
finalizare cu nota in catalog).
|
Conversatie
Explicatie
|
|
9. Tema pentru
acasa
|
Manual
Pagina 194 exercitiile de la 36 la 40.
|
Conversatie
|
Anexa. Fisa de lucru. Integrala definita a unei functii
continue
Folosind formula lui Leibniz -Newton
calculati urmatoarele integrale:


 (formula lui Leibniz
-Newton ).
(formula lui Leibniz
-Newton ). .
.

 este o
primitiva a lui f care se
anuleaza in t=a.
este o
primitiva a lui f care se
anuleaza in t=a.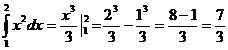
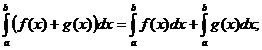




 .
.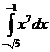 ;
; ;
;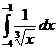 ;
;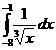 ;
; ;
;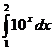 ;
;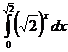 ;
;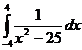 ;
;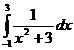 ;
; ;
;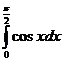 ;
; ;
;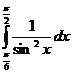 ;
;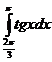 ;
;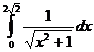 ;
;
 ;
;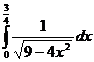 ;
;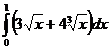 ;
;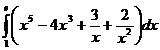 ;
;