didactic Clasa: a VII-a Matematica - Geometrie - Linii importante in triungi

Secventele

lectiei

Comp.

spec.

Activitati de invatare

Timp

Metode

Evaluare

1. Moment organizatoric

verificarea prezentei elevilor si notarea absentelor in catalog ;

- verificarea tinutei elevilor si celor necesare desfasurarii orei;

asigurarea unei atmosfere adecvate pentru buna desfasurare a orei;

2. Captarea atentiei

- verificarea temei elevilor prin sondaj, utilizand dialogul profesor-elev, elev-elev, prin confruntarea rezultatelor. In cazul in care apar diferente mari la rezultat se rezolva exercitiul la tabla;

Activitate comuna

Observare sistematica

3. Reactualizarea cunostintelor

C1

C2

Elevii vor raspunde la intrebarile:

- Care sunt tipurile de triunghiuri invatate?

- Care sunt liniile importante in triunghi invatate?

- Care sunt proprietatile liniilor importante in triunghi invatate?

Conversatia euristica

Analiza raspunsurilor

4. Informarea elevilor asupra lectiei noi

In cadrul orei de astazi vom recapitula liniile importante in triunghi invatate precum si proprietatile lor.

Explicatia

5. Dirijarea invatarii

C1

C2

C3

C4

Linii importante in triunghi

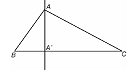
Sa consideram un triunghi fixat ABC.

1. Mediana

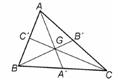
Definitie: Se numeste mediana a triunghiului ABC un segment care uneste un varf al Δ ABC cu mijlocul laturii opuse.Asadar exista trei mediane [AA'], [BB'], [CC'].

Teorema: Cele trei mediane ale unui triunghi sunt concurente (adica trec prin acelasi punct). Punctul lor comun se numeste centrul de greutate (sau baricentrul) triunghiului (notat cu G).

Punctul G este interior triunghiului ABC si este situat de fiecare mediana la o treime de baza si la doua treimi de varf.

Observatie: Mediana imparte un triunghi in doua triunghiuri de arii egale (triunghiuri echivalente).

2. Bisectoarea

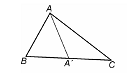
Definitie: Se numeste bisectoare a triunghiului ABC o bisectoare a unuia din unghiurile Δ ABC.

Asadar, exista trei bisectoare [AA' [BB' [CC'. Am notat cu A' punctul de intersectie al bisectoarei lui A cu latura [BC] etc.

Teorema: Cele trei bisectoare ale unui triunghi sunt concurente. Punctul lor comun se numeste centrul cercului inscris in triunghi.

3. Mediatoarea

Definitie: Se numeste mediatoare a triunghiului ABC o mediatoare a uneia din laturi.

De exemplu, mediatoarea lui [BC] se numeste mediatoarea laturii [BC].

Teorema: Cele trei mediatoare ale unui triunghi sunt concurente. Punctul lor comun se numeste centrul cercului circumscris triunghiului.

Remarca. Daca Δ ABC este dreptunghic in A, atunci centrul cercului circumscris Δ ABC coincide cu mijlocul ipotenuzei [BC].

4. Inaltimea

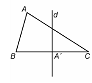
Definitie: Se numeste inaltime a unui triunghi o dreapta care trece printr-un varf al triunghiului si este perpendiculara pe latura opusa.

Teorema: Cele trei inaltimi ale unui triunghi sunt concurente. Punctul lor comun se numeste ortocentrul triunghiului.

5. Linia mijlocie intr-un triunghi

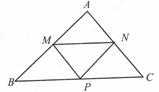
Definitie: Intr-un triunghi, segmentul determinat de mijloacele a doua laturi se numeste linie mijlocie.

Deci, in Δ ABC [MN], [MP] si [NP] sunt linii mijlocii.

Teorema: Segmentul care uneste mijloacele a doua laturi ale unui triunghi este paralel cu cea de a treia latura si are lungimea egala cu jumatate din lungimea acestei laturi.

Explicatia

Conversatia euristica

Observare sistematica

Analiza raspunsurilor

6. Asigurarea  feed-back-ului

C3

C4

Elevii rezolva pe caiete, individual problema 2 / pag 103 din manual

Munca independenta

Conversatia euristica

Exercitiul

Aprecieri verbale

Analiza raspunsurilor

7. Retentia si transferul

C1

Se face o scurta recapitulare a notiunilor dobandite.

Conversatia

Probe orale

8. Tema pentru acasa

Exercitiile 6, 7, 8, 9, 10 (Aplicatii) / pag. 103 din manual.

Conversatia

9. Aprecieri

se apreciaza elevii ce s au evidentiat in timpul orei

Conversatia

Aprecieri verbale