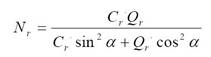Calculul barelor din lemn cu sectiune simpla

CALCULUL BARELOR DIN LEMN CU SECTIUNE SIMPLA

Bare solicitate la compresiune perpendiculara pe fibre

Capacitatea de rezistenta a elementelor din lemn masiv cu sectiune simpla, solicitate la compresiune perpendiculara pe directia fibrelor, Qr, in N, se stabileste cu relatia:

Q_r = R_cc┴ . A_c . m_T . m_r

in care:

R_cc┴ ­ rezistenta de calcul a lemnului masiv la compresiune perpendicular pe fibre, stabilita in functie de specia de material lemnos, clasa de calitate a lemnului si conditiile de exploatare a elementelor de constructie, in N/mm²;

A_c ­ aria de contact dintre cele doua elemente (aria reazemului) in mm²;

m_T ­ coeficientul de tratare a lemnului cu valorile specificate in tabelul 4.1;

m_r ­ coeficient de reazem, stabilit dupa cum urmeaza

Valorile coeficientului de reazem, mr

pentru elemente la care aria de contact este egala cu aria elementului comprimat (a), precum si la imbinari cu crestari laterale (b), m_r = 1,00;

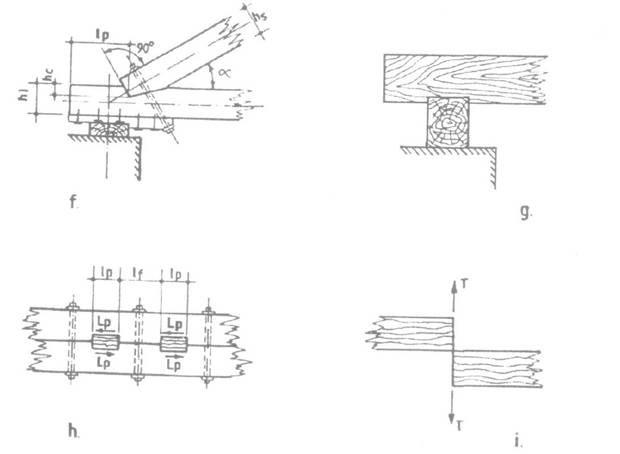
la piesele de rezemare (c si d), daca a ≥ h si a ≥ 10 cm, in imbinari cu pene prismatice care au fibrele dispuse normal pe fibrele elementelor imbinate (e), precum si la suprafetele de reazem ale constructiilor din lemn (g), m_r = 1,60;

la striviri sub saiba, m_r = 2,00.

Bare solicitate la strivire oblica

Capacitatea de rezistenta la strivire, N_r in N, cand forta la compresiune face un unghi α cu directia fibrelor (fig. 4.2, f) se determina cu relatia:

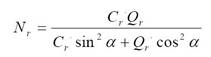
in care:

C_r ­ capacitatea de rezistenta a zonei comprimate (strivite), paralel cu directia fibrelor, care A_calcul este proiectia ariei de contact pe directia perpendiculara pe fibre;

Q_r ­ capacitatea de rezistenta a zonei comprimate (strivite), perpendicular pe directia fibrelor, in care A_c este proiectia ariei de contact pe directie perpendiculara fibrelor piesei care se striveste, iar m_r este coeficientul de reazem;

α ­ unghiul dintre directia fortei de compresiune (strivire) si directia fibrelor.

Bare solicitate la forfecare

forfecare perpendiculara pe fibre la grinzile incovoiate, solicitate de forte concentrate mari (i) sau la penele prismatice cu fibrele dispuse normal pe directia fibrelor pieselor imbinate (e)

forfecare in lungul fibrelor la imbinarile prin chertare pe lungimea pragurilor de forfecare (f) sau la penele prismatice cu fibrele dispuse in aceeasi directie cu fibrele elementelor imbinate (h).

Capacitatea de rezistenta la forfecare perpendiculara pe directia fibrelor elementelor din lemn masiv cu sectiune simpla, Vr, in N, se stabileste cu relatia:

Vr = R_cf┴ . A_f. m_T

in care:

R_cf┴ ­ este rezistenta la forfecare perpendiculara pe directia fibrelor stabilita in functie de specia de material lemnos,clasa de calitate a lemnului si conditiile de exploatare aelementelor de constructie, in N/mm²;

A_f ­ aria sectiunii care se foarfeca, egala cu aria piesei care preia efortul (aria sectiunii grinzii sau a penelor),in mm²;

m_T ­ coeficient de tratare a lemnului.

Capacitatea de rezistenta a pieselor din lemn masiv cu sectiune simpla la forfecare in lungul fibrelor, Fr, in N, se stabileste cu relatia:

F_r= R_cf|| . A_f . m_Tc / m_f

in care:

R_cf|| ­ rezistenta de calcul la forfecare paralela cu directii fibrelor, stabilita in functie de specia materialului lemnos, clasa de calitate a lemnului si conditiile de exploatare a elementelor de constructie, in N/mm²;

A_f ­ aria de forfecare, in mm²;

m_T ­ coeficientul de tratare;

m_f ­ coeficient de forfecare, care introduce raportul dintre lungimea pragului de forfecare si excentricitatea de aplicare a fortei fata de directia pragului, precum si modul de producere a forfecarii (unilaterala sau bilaterala).

Coeficientul de forfecare mf se calculeaza cu relatia:

m_f=1+β.l_p/e

in care:

β ­ coeficientul ce tine cont de tipul forfecarii, cu valoarea de 0,25 pentru forfecare unilaterala si 0,125 pentru forfecare bilaterala (fig. 4.3);

l_p ­ lungimea pragului de forfecare, limitata superior la 10 h_ch, in mm;

e ­ excentricitatea de aplicare a fortei de forfecare fata de axa neta a elementului, in mm.

Bare solicitate la incovoiere

Capacitatea de rezistenta a elementelor din lemn masiv cu sectiune simpla solicitate la incovoiere, M_r, in N mm se stabileste cu relatia:

M_r = R_ci . W_calcul . m_T

R_ci ­ rezistenta de calcul a lemnului masiv la incovoiere statica stabilita in functie de specia de material lemnos, clasa de calitate a lemnului si conditiile de exploatare a elementelor de constructie, in N/mm²;

W_calcul ­ modulul de rezistenta axial pentru sectiunea cea mai solicitata a elementului (W_brut daca elementul nu prezinta slabiri in sectiunea de calcul, respectiv W_net daca elementul are slabiri in zona de calcul);

m_T ­ coeficientul de tratare a lemnului.

La elementele incovoiate se verifica in mod obligatoriu si conditia de rigiditate (deformatie), cu relatia:

f_{max,final ≤} f_adm

f_max,final ­ deformatia maxima finala din incovoiere;

f_adm ­ deformatia maxima admisa, cu valorile din tabel.

Bare solicitate la intindere si incovoiere (intindere excentrica)

Barele simple din lemn masiv solicitate la intindere excentrica se verifica cu relatia:

T_ef este incarcarea axiala de calcul in bara, in N;

T_r ­ capacitatea de rezistenta a barei la intindere centrica, in N;

M_ef ­ momentul incovoietor de calcul, stabilit in raport cu axa centrala de inertie perpendiculara pe directia de actiune a fortei, in Nmm;

M_r ­ capacitatea de rezistenta a barei la incovoiere in raport cu aceeasi axa, in Nmm.

Bare solicitate la compresiune si incovoiere (compresiune excentrica)

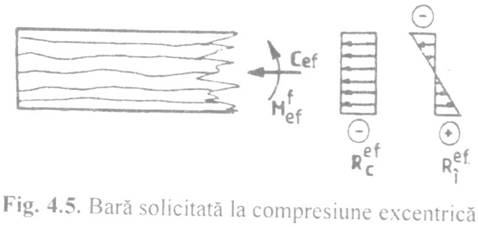
Barele simple din lemn masiv solicitate la compresiune excentrica se verifica in raport cu axa perpendiculara pe directia fortelor ce produc incovoierea (x-­x, in fig. 4.5), cu relatia:

C_ef- este efortul axial de calcul in bara, in N;

C_r ­ capacitatea de rezistenta a barei la compresiune, in N:

M^f_ef ­ momentul incovoietor maxim final stabilit in raport cu axa centrala principala de inertie, perpendiculara pe directia de actiune a fortei, in Nmm;

M_r ­ capacitatea de rezistenta a barei la incovoiere in raport cu aceeasi axa, in Nmm.

Momentul incovoietor efectiv final se calculeaza tinand cont de momentul incovoietor secundar (moment de ordinul 2) produs de forta axiala de compresiune care actioneaza excentric fata de axa barei, cu relatia:

in care:

E _0,05 ­ modulul de elasticitate caracteristic, cu valorile din tabelul 2.4, in functie de specia de material lemnos utilizata, in N/mm²;

m_uE ­ coeficient al conditiilor de lucru, cu valorile date in tabelul 2.5, in functie de esenta si de clasa de exploatare a elementului de constructie din lemn care se proiecteaza;

m_T ­ coeficient de tratare a lemnului cu valorile specificate in tabelul 4.1;

I ­ momentul de inertie axial in raport cu axa perpendiculara pe directia de aplicare a fortelor ce produc incovoierea, in mm⁴ ;

l_f ­ lungimea de flambaj a barei, in mm.