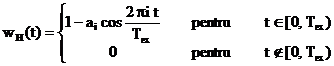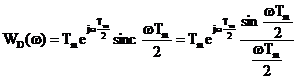Functii fereastra
In acest
capitol se introduce notiunea de semnal quasiperiodic (semnal cu aspect
periodic) si se arata ca semnalele periodice prelevate din
natura nu au modele matematice analitice, dar aceste semnale au spectre
discrete care pot fi calculate cu algoritmul FFT.
In
capitolul 2 trunchierea in timp a semnalului analizat s‑a facut prin
ponderare cu o functie fereastra rectangulara. In continuare se
studiaza alte functii fereastra care reduc diferenta dintre
cazul cel mai favorabil si cel mai putin favorabil si reduc
influenta lobilor secundari asupra amplitudinii liniilor spectrale.
Introducere
In
capitolul 2 s‑a discutat influenta trunchierii in timp asupra
spectrului de linii rezultat in urma transformatei analizei unui semnal
armonic cu ajutorul transformatei Fourier discrete. Semnalul armonic 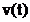 a fost esantionat
si trunchiat in timp prin ponderarea cu functia
fereastra rectangulara
a fost esantionat
si trunchiat in timp prin ponderarea cu functia
fereastra rectangulara 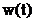 . Aplicand formulele 2.13 si 2.15 se obtine
secventa
. Aplicand formulele 2.13 si 2.15 se obtine
secventa
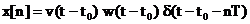 , (4.1)
, (4.1)
unde 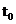 este momentul in care
incepe achizitia datelor,
este momentul in care
incepe achizitia datelor, 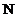 este numarul de
esantioane prelevat din semnalul
este numarul de
esantioane prelevat din semnalul 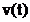 iar
iar 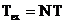 este durata functiei
fereastra
este durata functiei
fereastra 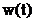 .
.
Secventa 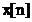 este analizata
prin Transformata Fourier Discreta (implementata prin algoritmul
FFT). Se obtine spectrul esantionat
este analizata
prin Transformata Fourier Discreta (implementata prin algoritmul
FFT). Se obtine spectrul esantionat
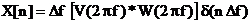 . (4.2)
. (4.2)
In figurile 2.7, 2.8 si 2.9 se
observa ca semnalul armonic 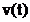 are un spectru discret
cu o singura linie spectrala, iar functia
fereastra
are un spectru discret
cu o singura linie spectrala, iar functia
fereastra 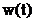 are un spectru
continuu. Produsul de convolutie
are un spectru
continuu. Produsul de convolutie 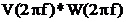 ingroasa
linia spectrala din spectrul continuu si produce diferentele
dintre cazul favorabil si cazul cel mai putin favorabil din spectrul
esantionat.
ingroasa
linia spectrala din spectrul continuu si produce diferentele
dintre cazul favorabil si cazul cel mai putin favorabil din spectrul
esantionat.
Lobii secundari ai functiei fereastra
In Figura 2.6
se prezinta forma functiei de densitate spectrala a
ferestrei rectangulare 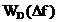 (fereastra Dirichlet).
In figura se observa ca functia are un lob principal cu
latimea
(fereastra Dirichlet).
In figura se observa ca functia are un lob principal cu
latimea 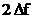 si multi
lobi secundari cu latimea
si multi
lobi secundari cu latimea 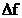 . In figurile 2.8 si 2.9 se prezinta functiile
de densitate spectrala ale unui semnal sinusoidal, cu amplitudinea de
. In figurile 2.8 si 2.9 se prezinta functiile
de densitate spectrala ale unui semnal sinusoidal, cu amplitudinea de 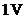 , trunchiat in timp cu o fereastra rectangulara.
, trunchiat in timp cu o fereastra rectangulara.
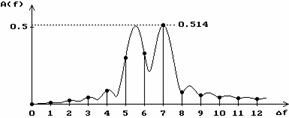
In cazul cel mai favorabil prezentat in
Figura 2.8 se observa ca lobii secundari nu au im pentru ca in
urma esantionarii in frecventa a functiei de densitate
spectrala ramane doar o pereche de linii spectrale cu amplitudinea de
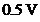 si
frecventele
si
frecventele 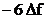 si
si 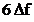 . Partea negativa a axei frecventei nu a fost
reprezentata grafic.
. Partea negativa a axei frecventei nu a fost
reprezentata grafic.
In cazul cel mai putin favorabil
prezentat in Figura 2.9 se observa ca in spectru exista
doua linii spectrale egale cu frecventele de 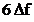 si
si 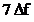 , iar valoarea amplitudinii acestor linii spectrale este de
, iar valoarea amplitudinii acestor linii spectrale este de
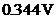 , adica
, adica 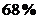 din valoarea
adevarata si ca datorita lobilor secundari ai
functiei de densitate spectrala
din valoarea
adevarata si ca datorita lobilor secundari ai
functiei de densitate spectrala 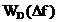 apar componente spectrale care nu au
semnificatie fizica. Amplitudinea maxima a acestor componente
este de
apar componente spectrale care nu au
semnificatie fizica. Amplitudinea maxima a acestor componente
este de 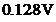 adica
adica 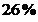 din valoarea
adevarata.
din valoarea
adevarata.
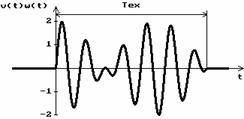
Figura
4.1. Spectrul unei sume de doua semnale armonice
Rezultatele
din capitolul 2 pot fi imediat extinse asupra semnalelor periodice care au spectre
de linii sau asupra combinatiilor de semnale armonice. In figura 4.1 se
prezinta forma de unda a unei sume de semnale armonice cu
frecventele  si
si 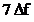 .
.
Cele doua semnale armonice au
amplitudinea de 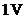 deci in partea
pozitiva a spectrului ar trebui sa se gaseasca doua
linii spectrale cu amplitudinea de
deci in partea
pozitiva a spectrului ar trebui sa se gaseasca doua
linii spectrale cu amplitudinea de 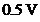 . In realitate linia spectrala cu frecventa
. In realitate linia spectrala cu frecventa 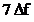 are amplitudinea mai
mare de
are amplitudinea mai
mare de 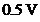 pentru ca se
suprapune cu amplitudinea primului lob secundar al spectrului semnalului cu
frecventa de
pentru ca se
suprapune cu amplitudinea primului lob secundar al spectrului semnalului cu
frecventa de 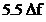 .
.
Semnale quasiperiodice
Pana
in prezent s‑au analizat numai semnale analitice adica semnale
descrise prin modele matematice compuse dintr‑un numar finit de
functii algebrice sau trigonometrice simple. Achizitia datelor
este o succesiune de trei operatii: esantionare, cuantizare si
trunchiere in timp. Semnalele prelevate din natura si transferate
in calculator prin achizitia datelor nu au modele matematice analitice.
Semnalele
cu aspect periodic carora nu li se cunoaste exact frecventa se
numesc semnalele quasiperiodice.
Pentru
semnalele quasiperiodice nu se poate verifica conditia de periodicitate
(2.2) ci doar se poate formula o ipoteza de periodicitate. Notiunile
"perioada principala" notata 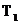 si
"frecventa fundamentala" notata
si
"frecventa fundamentala" notata 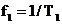 isi
pastreaza sensul definit in sectiunea 2.1.1. Semnalele quasiperiodice esantionate si trunchiate in timp
pot fi analizate cu transformata Fourier discreta.
isi
pastreaza sensul definit in sectiunea 2.1.1. Semnalele quasiperiodice esantionate si trunchiate in timp
pot fi analizate cu transformata Fourier discreta.
Functii de ponderare de tip "cosinus insumat"
Functiile
de ponderare de tip "cosinus insumat" au doua avantaje: au expresii
analitice simple iar performantele lor pot fi analizate cu metoda dezvoltata
din sectiunile 2.3.1 unde se prezinta analiza ferestrei Dirichlet
si 2.3.2 unde se analizeaza o portiune de semnal armonic.
Functia 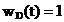 pentru
pentru 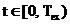 si
si 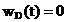 in rest se numeste
fereastra rectangulara sau fereastra Dirichlet. Forma
functiilor de ponderare de tip "cosinus insumat" se calculeaza cu
formula
in rest se numeste
fereastra rectangulara sau fereastra Dirichlet. Forma
functiilor de ponderare de tip "cosinus insumat" se calculeaza cu
formula
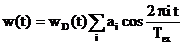 (4.3)
(4.3)
unde inmultirea cu 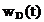 anuleaza
functiile
anuleaza
functiile 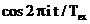 pentru
pentru 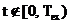 , deci functia de ponderare
, deci functia de ponderare 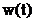 facen si
trunchierea in timp a semnalului analizat
facen si
trunchierea in timp a semnalului analizat 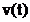 . Coeficientii
. Coeficientii 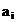 sunt:
sunt:
|
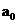
|
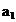
|
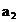
|
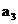
|
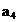
|
|
Dirichlet
|
|
|
|
|
|
|
Hanning
|
|
|
|
|
|
|
Kaiser-Bessel
|
|
|
|
|
|
|
Flat
Top
|
|
|
|
|
|
Tabelul 4.1. Coeficientii 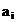
Din (4.__) rezulta ca fereastra
Dirichlet face si ea parte din categoria functiilor fereastra de
tip "cosinus insumat" si ca spectrul ferestrei Dirichlet este o
componenta a spectrului celorlalte functii din aceasta
categorie.
Figura
4.1. Metoda de calcul a indecsilor 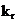 ,
, 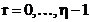
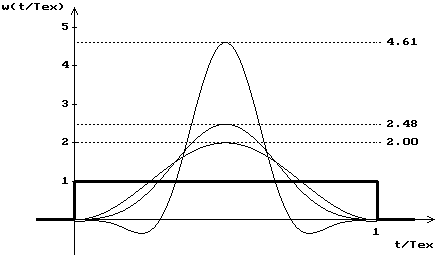
In figura 4.1 se prezinta forma
functiilor fereastra calculata cu formula (4.__) si coeficientii
din tabelul 4.1. Pe abscisa s‑a reprezentat timpul normat 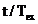 iar pe ordonata
functia
iar pe ordonata
functia 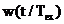 . Fereastra Dirichlet este reprezentata cu linie
groasa. In ordinea crescatoare a maximelor sunt reprezentate
ferestrele Hanning, Kaiser‑Bessel si Flat Top.
. Fereastra Dirichlet este reprezentata cu linie
groasa. In ordinea crescatoare a maximelor sunt reprezentate
ferestrele Hanning, Kaiser‑Bessel si Flat Top.
|
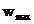
|
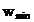
|
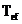
|
|
Dirichlet
|
|
|
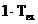
|
|
Hanning
|
|
|
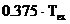
|
|
Kaiser-Bessel
|
|
|
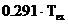
|
|
Flat
Top
|
|
|
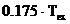
|
Tabelul 4.2. Amplitudinea maxima, amplitudinea minima si
durata efectiva a functiilor de ponderare de tip "cosinus insumat"
Se observa ca pentru 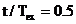 celelalte functii
de ponderare au un maxim.
celelalte functii
de ponderare au un maxim.
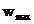 si
si 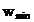
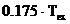
fereastra Hanning are 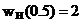 , fereastra
, fereastra
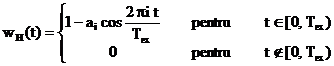 (2.7)
(2.7)
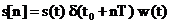 ,
, 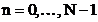 (2.7)
(2.7)
Se pune problema gasirii unor
functii altor functii de ponderare de forma 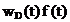 care sa
reduca diferentele dintre cazul favorabil si cel defavorabil.
care sa
reduca diferentele dintre cazul favorabil si cel defavorabil.
Functia 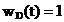 , pentru
, pentru 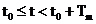 si
si 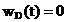 in rest se
numeste fereastra rectangulara sau fereastra Dirichlet
(v. formula (2__), sectiunea 2.__). Se pune problema gasirii unor
functii altor functii de ponderare de forma
in rest se
numeste fereastra rectangulara sau fereastra Dirichlet
(v. formula (2__), sectiunea 2.__). Se pune problema gasirii unor
functii altor functii de ponderare de forma 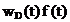 care sa
reduca diferentele dintre cazul favorabil si cel defavorabil.
care sa
reduca diferentele dintre cazul favorabil si cel defavorabil.
Functii de ponderare
Fie semnalul 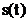 si secventa
si secventa 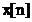 prelevata din
semnalul
prelevata din
semnalul 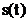 esantionat cu
perioada
esantionat cu
perioada 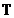
este
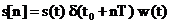 ,
, 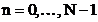 (2.7)
(2.7)
Au fost studiate multe tipuri de functii
de ponderare
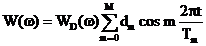 (2.7)
(2.7)
Spectrul ferestrei Dirichlet
Spectrul functiei fereastra
Dirichlet din figura este:
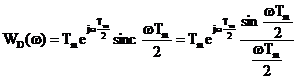 (2.7)
(2.7)
unde N este numarul de esantionare
memorat in vectorul 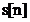 , iar regula de indexare folosita in transformata
Fourier discreta este
, iar regula de indexare folosita in transformata
Fourier discreta este 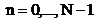 .
.