Legea conservarii sarcinii electrice
Este o lege generala. Pentru corpuri
izolatoare este data de rel. (2.1.30). Astfel, daca se considera
o suprafata inchisa 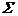 a unui corp izolator
electrizat, astfel incat aceasta sa nu fie strabatuta de
curent electric de conductie, se constata, experimental, ca
sarcina totala localizata in interiorul suprafetei ramane
constanta:
a unui corp izolator
electrizat, astfel incat aceasta sa nu fie strabatuta de
curent electric de conductie, se constata, experimental, ca
sarcina totala localizata in interiorul suprafetei ramane
constanta:
|
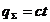 . .
|
|
Daca insa
suprafata 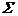 este
strabatuta si de conductoare parcurse de curenti
electrici de conductie, sarcina electrica variaza in timp,
conform interpretarii fizice date acestor curenti, expresia legii
fiind data de rel. (2.1.31).
este
strabatuta si de conductoare parcurse de curenti
electrici de conductie, sarcina electrica variaza in timp,
conform interpretarii fizice date acestor curenti, expresia legii
fiind data de rel. (2.1.31).
Sa
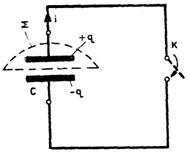
consideram, de exemplu, un condensator electric incarcat cu sarcina q, ale carui armaturi se
leaga printr-un conductor metalic (fig. 2.1.7). In interiorul
conductorului potentialul nu mai poate ramane constant
(armaturile au potentiale diferite) si echilibrul electrostatic
nu se mai mentine la inchiderea circuitului. In timpul regimului
tranzitoriu de descarcare a condensatorului, prin conductor va trece un
curent electric, care este egal cu viteza de scadere in timp a sarcinii de
pe armaturile condensatorului.
|
|
|
Fig. 2.1.7 Descarcarea
unui condensator electric
|
Generalizand problema,
se poate enunta legea conductiei electrice sub forma
integrala: intensitatea 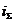 a curentului electric
de conductie care iese dintr-o
suprafata inchisa
a curentului electric
de conductie care iese dintr-o
suprafata inchisa 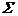 , atasata conductoarelor parcurse de curent,
este egala, in fiecare moment, cu viteza de scadere a sarcinii
, atasata conductoarelor parcurse de curent,
este egala, in fiecare moment, cu viteza de scadere a sarcinii 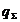 , localizate in interiorul suprafetei.
, localizate in interiorul suprafetei.
Relatia de definitie a legii este
urmatoarea:
Conventie: curentul 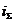 trebuie considerat
pozitiv daca iese din suprafata
trebuie considerat
pozitiv daca iese din suprafata 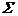 si negativ
daca intra, fiind asociat, prin conventie, cu sensul pozitiv al
normalei
si negativ
daca intra, fiind asociat, prin conventie, cu sensul pozitiv al
normalei  la suprafata
elementara
la suprafata
elementara 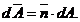
Relatia de mai sus poate fi pusa
si sub forma:
Pentru forma locala a legii se
aplica teorema Gauss - Ostrogradski membrului I al
relatiei (2.1.32):
Tinand seama de expresia din membrul
drept al aceleiasi relatii, se obtine:
Relatia (2.1.34)
reprezinta forma locala a legii conservarii sarcinii electrice
pentru circuite imobile.
Daca mediul
analizat este in miscare (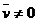 ), in conductoare apare un curent suplimentar - curentul de convectie, astfel incat
legea sub forma integrala devine:
), in conductoare apare un curent suplimentar - curentul de convectie, astfel incat
legea sub forma integrala devine:


