Legea
fluxului magnetic
In orice moment fluxul
magnetic prin orice suprafata inchisa 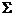 este nul:
este nul:
Este o lege
generala. Legea fluxului magnetic exprima, ca sens fizic, inexistenta sarcinilor magnetice.
Conform acesteia,
fluxul magnetic ce intra printr-o parte a suprafetei 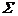 este egal cu cel
care iese prin alta parte, in acelasi moment, cu conditia ca in
interiorul suprafetei sa nu existe alte surse de camp magnetic.
este egal cu cel
care iese prin alta parte, in acelasi moment, cu conditia ca in
interiorul suprafetei sa nu existe alte surse de camp magnetic.
Relatia (2.1.9)
reprezinta forma generala (integrala) a legii. Pentru a
obtine forma locala, se aplica teorema divergentei (teorema
Gauss - Ostrogradski) relatiei
(2.1.9) :
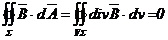
de unde rezulta:
|
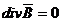 sau sau 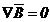
|
|
Ca urmare,
inductia magnetica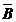 este un vector camp
solenoidal (fara surse, rotational) de forma
este un vector camp
solenoidal (fara surse, rotational) de forma 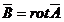 sau
sau 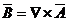 .
.
Marimea 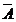 se numeste potential magnetic vector al
campului magnetic, fara a avea o semnificatie fizica; este
o marime de calcul.
se numeste potential magnetic vector al
campului magnetic, fara a avea o semnificatie fizica; este
o marime de calcul.
Fluxul magnetic devine in acest caz:
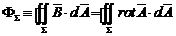
Aplicand teorema lui Stokes relatiei de
mai sus, aceasta capata forma:
Relatia (2.1.11)
este o alta expresie a legii fluxului magnetic, care arata ca
fluxul magnetic are aceeasi valoare prin orice suprafata
deschisa 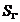 care se sprijina
pe un contur inchis
care se sprijina
pe un contur inchis 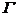 . Fluxul magnetic depinde numai de conturul
. Fluxul magnetic depinde numai de conturul 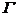 si nu de forma
suprafetei care se sprijina pe el.
si nu de forma
suprafetei care se sprijina pe el.
Precizare
La calculul lui 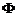 cu
cu 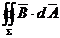 , este necesar sa se cunoasca valorile
inductiei
, este necesar sa se cunoasca valorile
inductiei 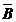 in toate punctele
suprafetei
in toate punctele
suprafetei 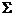 .
.
La calculul lui 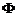 cu
cu 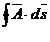 , este suficient sa se cunoasca valorile lui
, este suficient sa se cunoasca valorile lui 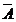 doar pe conturul care
limiteaza suprafata
doar pe conturul care
limiteaza suprafata 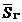 , deci rezolvarea problemei se simplifica.
, deci rezolvarea problemei se simplifica.

