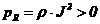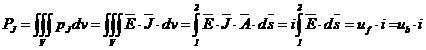Legea transformarii energiei in conductoare parcurse
de curent electric de conductie (legea Joule-
Lenz)
Este o lege generala.Forma locala a
legii este urmatoarea:
Puterea instantanee a campului electromagnetic
transformata in caldura pe unitatea de volum a unui conductor
parcurs de curent electric de conductie este data de produsul scalar dintre intensitatea campului electric
(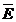 ) si densitatea de curent (
) si densitatea de curent (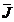 ) , din conductor, in punctul( volumul infinitezimal ) in
care se calculeaza aceasta:
) , din conductor, in punctul( volumul infinitezimal ) in
care se calculeaza aceasta:
In cazul
conductoarelor liniare, izotrope si omogene, fara surse, vectorii
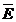 si
si 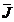 sunt omoparaleli
si cum, conform legii conductiei electrice
sunt omoparaleli
si cum, conform legii conductiei electrice 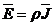 , pentru aceste conductoare se obtine expresia:
, pentru aceste conductoare se obtine expresia:
Marimea  se mai numeste densitatea
de volum a puterii transformate ireversibil in caldura
prin efect Joule - Lenz, in conductor.
se mai numeste densitatea
de volum a puterii transformate ireversibil in caldura
prin efect Joule - Lenz, in conductor.
Daca conductorul
este neomogen (contine surse de energie electrica, de tipul
acumulatorului electric), din legea conductiei electrice 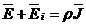 se determina
se determina

Inlocuind pe 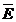 in relatia lui
in relatia lui  se obtine:
se obtine:
In aceasta relatie:
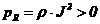
este partea din puterea
electromagnetica primita de conductor de la retea, in unitatea
de timp, si transformata ireversibil in caldura pe unitatea
de volum a conductorului ( independent de sensul curentului), iar marimea:
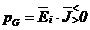
este partea din puterea
electromagnetica schimbata intre sursa din latura (cand aceasta
sursa exista) si campul electromagnetic.
In cazul in care 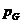 >0, vectorii
>0, vectorii 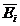 si
si  sunt omoparaleli (au
acelasi sens) si
sunt omoparaleli (au
acelasi sens) si 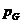 este cedata de sursa si primita de latura.
este cedata de sursa si primita de latura.
In cazul in care 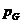 <0, vectorii
<0, vectorii 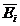 si
si  sunt antiparaleli
si
sunt antiparaleli
si 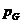 este primita de
sursa si cedata de latura (cazul incarcarii unui acumulator de
la retea). In acest caz, in rel. (2.1.26) termenul
este primita de
sursa si cedata de latura (cazul incarcarii unui acumulator de
la retea). In acest caz, in rel. (2.1.26) termenul 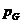 intra cu semnul plus.
intra cu semnul plus.
Sub forma
integrala, legea se obtine integrand relatia (2.1.24) pe
intregul volum (V) al unui conductor.
Se obtine expresia puterii totale, 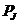 , cedate de
campul electromagnetic unei laturi sau unui segment omogen de circuit (fig.2.1.4):
, cedate de
campul electromagnetic unei laturi sau unui segment omogen de circuit (fig.2.1.4):
|

|
|
Fig.2.1.4 Segment omogen de
circuit (conductor)
|
unde:
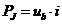 - reprezinta
puterea totala cedata de retea circuitului.
- reprezinta
puterea totala cedata de retea circuitului.
In cazul in care in
latura de circuit receptoare exista si o sursa de t.e.m.,
tinand cont de ecuatia laturii,  , relatia (2.1.19) devine:
, relatia (2.1.19) devine:
unde: 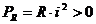 corespunde
transformarii ireversibile a energiei electromagnetice in
caldura prin efect Joule-Lenz,
la nivelul intregii laturi de circuit;
corespunde
transformarii ireversibile a energiei electromagnetice in
caldura prin efect Joule-Lenz,
la nivelul intregii laturi de circuit;
 corespunde
transformarii energiei chimice a sursei in energie electrica (sursa cedeaza
energie), la nivelul intregii laturi de
circuit;
corespunde
transformarii energiei chimice a sursei in energie electrica (sursa cedeaza
energie), la nivelul intregii laturi de
circuit;
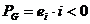 corespunde
transformarii energiei electrice din conductor in energie chimica
(sursa preia energie de la circuit, adica se incarca).
corespunde
transformarii energiei electrice din conductor in energie chimica
(sursa preia energie de la circuit, adica se incarca).
Sensul puterii in
circuit (latura de circuit) este dat de relatia de sensuri dintre ei si i:
daca
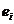 si
si  au acelasi sens,
atunci
au acelasi sens,
atunci 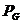 >0 si sursa
cedeaza energie laturii de circuit, deci latura este generatoare (fig.
2.1.5):
>0 si sursa
cedeaza energie laturii de circuit, deci latura este generatoare (fig.
2.1.5):
|

|
|
Fig. 2.1.5 Latura
generatoare
|
- daca 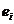 si
si  au sensuri opuse,
atunci
au sensuri opuse,
atunci 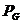 <0 si sursa
primeste energie de la latura/circuit, deci latura este receptoare (consumatoare);
este cazul incarcarii unui acumulator (fig.2.1.6):
<0 si sursa
primeste energie de la latura/circuit, deci latura este receptoare (consumatoare);
este cazul incarcarii unui acumulator (fig.2.1.6):
|

|
|
Fig. 2.1.6. Latura
receptoare
|