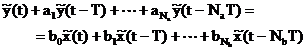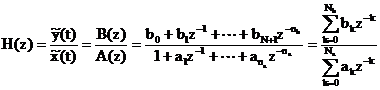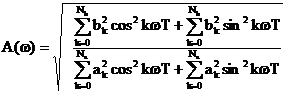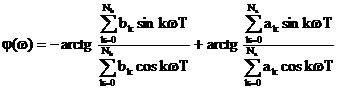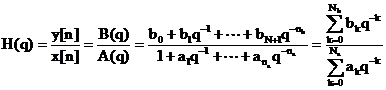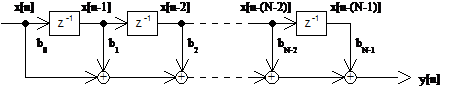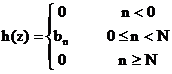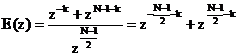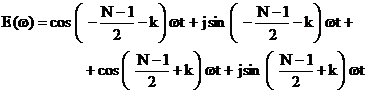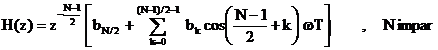Metoda de proiectare a filtrelor FIR cu faza liniara
In acest
capitol se prezinta pe scurt ecuatia in diferente, functia
de transfer si functia pondere ale unui a unui filtru digital. Apoi
se particularizeaza aceste pentru filtrele fir si se prezinta o metoda
de calcul a parametrilor unui filtru FIR pornind de la forma unei functii
fereastra cunoscute.
Filtre
digitale
In Figura
5.1 se prezinta schema bloc a unui DSP (Digital Signal Processor) care este filtru analogic
cu implementare digitala.

Figura
5.1. Schema bloc a filtrului digital
In
schema 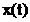 si
si  sunt semnalele
analogice de intrare si de iesire ale filtrului,
sunt semnalele
analogice de intrare si de iesire ale filtrului, 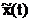 si
si 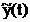 sunt semnale analogice
sunt semnale analogice
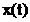 si
si  esantionate cu
perioada T .
esantionate cu
perioada T .
Filtrul
digital din Figura 5.1 functioneaza in timp real (on‑line).
Functionarea filtrului digital este descrisa de ecuatia in
diferente
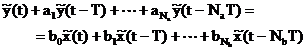 , (5.1)
, (5.1)
unde 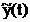 este valoarea
esantionului curent al semnalului de iesire. Din ecuatia (5.1)
se poate explicita functia de filtrare, sau formula de calcul al valorii
esantionului curent al semnalului
de iesire:
este valoarea
esantionului curent al semnalului de iesire. Din ecuatia (5.1)
se poate explicita functia de filtrare, sau formula de calcul al valorii
esantionului curent al semnalului
de iesire:
 . (5.2)
. (5.2)
Formula
(5.2) se citeste:
"Valoarea esantionului curent al
semnalului de iesire se calculeaza din valorile anterioare ale
esantioanelor semnalului de iesire si din valorile
curenta si anterioare ale esantioanelor semnalului de
intrare".
Formula
(5.2) este importanta pentru ca da cea mai comoda cale de
scriere a unui program care implementeaza un filtru digital care
functioneaza in timp real (on‑line
Daca
se aplica transformata Z ecuatiei in diferente (5.1) se
obtine ecuatia discreta
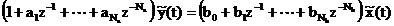 , (5.3)
, (5.3)
unde 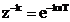 este operatorul de
intarziere cu k perioade de esantionare. In ecuatia discreta
(5.3) esantionate
este operatorul de
intarziere cu k perioade de esantionare. In ecuatia discreta
(5.3) esantionate 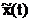 si
si 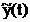 sunt imaginile prin
transformata Z ale semnalelor analogice
sunt imaginile prin
transformata Z ale semnalelor analogice 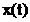 si
si  . Evident functia de filtrare (5.2) poate fi pusa
si sub forma:
. Evident functia de filtrare (5.2) poate fi pusa
si sub forma:
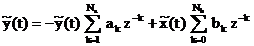 . (5.4)
. (5.4)
Prin
calculul raportului dintre imaginile 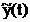 si
si 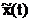 din ecuatia
discreta (5.3) se obtine functia de transfer a filtrului
digital:
din ecuatia
discreta (5.3) se obtine functia de transfer a filtrului
digital:
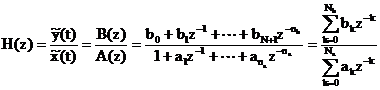 , (5.5)
, (5.5)
Din notatia 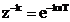 , dupa trecerea din transformata Laplace in transformata
Fourier, prin aplicarea formulei lui Euler se obtine:
, dupa trecerea din transformata Laplace in transformata
Fourier, prin aplicarea formulei lui Euler se obtine:
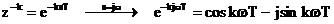 . (5.6)
. (5.6)
Daca se substituie (5.5) in (5.4)
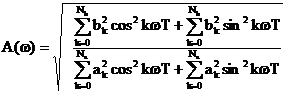 , (5.7)
, (5.7)
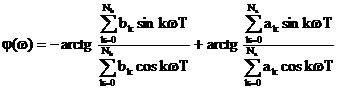 , (5.8)
, (5.8)
In momentul
in care se implementeaza filtrul digital printr‑un program, perioada
de esantionare T nu mai are semnificatie fizica explicita.
In acest caz:
perioada de esantionare se normeaza la un tact 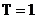
secventele de intrare si de iesire ale filtrului digital
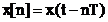 si
si  se memoreaza sub
forma unor vectori;
se memoreaza sub
forma unor vectori;
operatorul 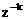 cu semnificatia "
intarziere cu k perioade de esantionare" se inlocuieste cu operatorul
cu semnificatia "
intarziere cu k perioade de esantionare" se inlocuieste cu operatorul
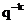 care are
semnificatia "intarziere cu k tacte".
care are
semnificatia "intarziere cu k tacte".
In aceste
conditii functia de filtrare normata este:
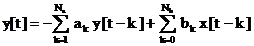 . (5.9)
. (5.9)
Substituind
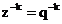 in (5.5) se
obtine functia de transfer normata:
in (5.5) se
obtine functia de transfer normata:
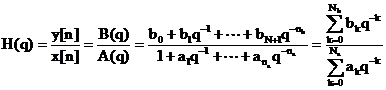 , (5.10)
, (5.10)
unde  si
si  sunt esantioanele
curente ale semnalelor de intrare si de iesire iar
sunt esantioanele
curente ale semnalelor de intrare si de iesire iar 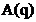 si
si  sunt polinoame.
sunt polinoame.
Filtre
FIR
Un filtru digital care are 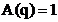 se numeste filtru
digital de tip FIR (Finite
Impulse response). Functia de filtrare a
filtrului FIR este:
se numeste filtru
digital de tip FIR (Finite
Impulse response). Functia de filtrare a
filtrului FIR este:
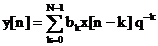 , (5.11)
, (5.11)
unde  si
si 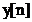 , sunt secventele de intrare si de iesire ale
unui filtrului digital,
, sunt secventele de intrare si de iesire ale
unui filtrului digital, 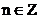 si
coeficientii
si
coeficientii 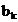 ,
, 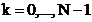 , sunt coeficientii filtrului digital. Filtrul se
implementeaza prin urmatorul graful de fluenta din Figura
5.2.
, sunt coeficientii filtrului digital. Filtrul se
implementeaza prin urmatorul graful de fluenta din Figura
5.2.
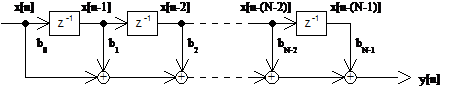
Figura
5.2. Filtrul FIR
Functia
de transfer a filtrului este:
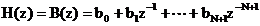 . (5.12)
. (5.12)
Fie functia pondere discreta
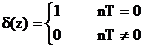 , (5.13)
, (5.13)
raspunsul filtrului FIR la functia
delta discreta este functia pondere discreta este data de
coeficientii filtrului FIR (5.12)
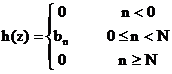 , (5.14)
, (5.14)
Transformarea
unui filtru IIR intr‑un filtru FIR echivalent
Fie filtrul IIR de ordinul 1
 . (5.15)
. (5.15)
Orice filtru IIR poate fi transformat intr‑un
filtru FIR prin metoda impartirii continue prezentata in Figura
5.3

Figura
5.3 Metoda impartirii continue
Se spune ca impartirea continua
este convergenta daca coeficientii filtrului FIR scad odata
cu cresterea exponentului 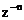 . Daca filtrul are un pol in apropierea cercului unitar
atunci convergenta este slaba. Daca filtrul are un pol pe cercul
unitar sau in afara lui impartirea nu este convergenta dar nici
filtrul IIR nu este stabil.
. Daca filtrul are un pol in apropierea cercului unitar
atunci convergenta este slaba. Daca filtrul are un pol pe cercul
unitar sau in afara lui impartirea nu este convergenta dar nici
filtrul IIR nu este stabil.
Teoretic
filtrul FIR echivalent are un numar infinit de coeficienti, dar in
practica rezultatul impartirii se truncheaza. Intotdeauna
filtrul FIR echivalent are mai multi coeficienti decat filtrul IIR
din care a fost obtinut.
Filtre
FIR cu faza liniara
Fie un filtru FIR cu proprietatea 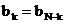 ,
, 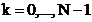
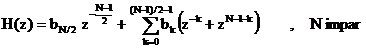 (5.16)
(5.16)
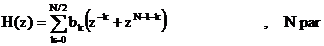 (5.17)
(5.17)
Din relatiile lui Euler rezulta
ca
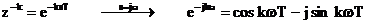 , (5.18)
, (5.18)
unde 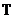 este perioada de
esantionare. Se calculeaza expresia:
este perioada de
esantionare. Se calculeaza expresia:
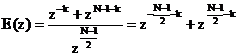 , (5.19)
, (5.19)
de unde prin substitutia 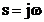
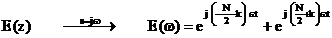 , (5.20)
, (5.20)
In aceste conditii
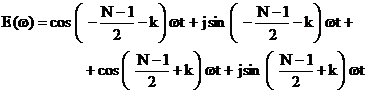 , (5.21)
, (5.21)
se observa ca termenii imaginari se
reduc si ca expresia finala este:
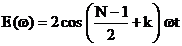 , (5.22)
, (5.22)
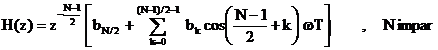 (3.23)
(3.23)
 (5.24)
(5.24)
Problema
Se da o secventa  esantionat cu
frecventa de
esantionat cu
frecventa de  . Sa se proiecteze un filtru trece jos de tip FIR care
sa aiba
. Sa se proiecteze un filtru trece jos de tip FIR care
sa aiba 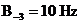 si caracteristica
de frecventa a ferestrei Hanning.
si caracteristica
de frecventa a ferestrei Hanning.
Din tabelul __ aflam 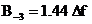 pentru fereastra
Hanning.
pentru fereastra
Hanning.
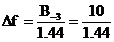 (5.25)
(5.25)
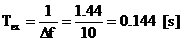 (5.26)
(5.26)
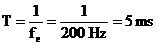 (5.27)
(5.27)
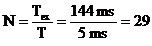 (5.28)
(5.28)
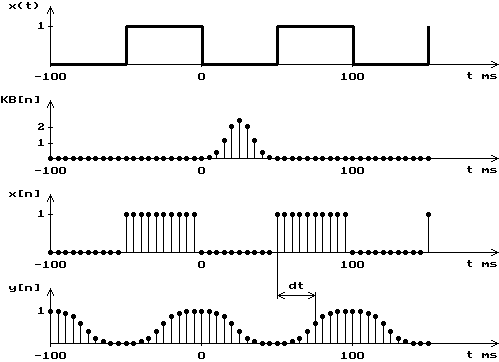
Filtru
FIR KB‑10 windov