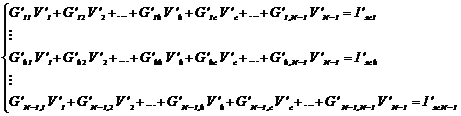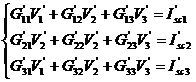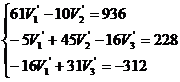Metoda potentialelor de/la noduri
In cazul metodei
potentialelor de noduri se opereaza cu (N-1) variabile, mai putine fata de cele utilizate
in cazul metodei curentilor de ochiuri, respectiv, al metodei teoremelor
lui Kirchhoff:
(N-1) < 0 < L
Noile variabile sunt potentialele nodurilor
independente sau diferentele de potential dintre fiecare nod al
retelei si un nod (al N-lea),
ales arbitrar ca referinta (potential
de referinta), considerat in mod obisnuit ca fiind legat la pamant (VN = 0).
|
|
|
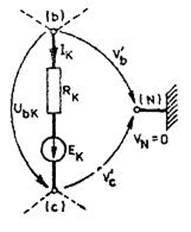
Fig. 4.4.19 Latura de circuit
|
Fie latura de circuit
din figura 4.4.19, apartinand nodurilor (b) si (c) si
nodul N al retelei, cu rol de
referinta. Conform primei teoreme a lui Kirchhoff se poate scrie pentru nodul (b):
|
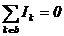 , b = 1,2,.,N-1 , b = 1,2,.,N-1
|
|
Ecuatia
de functionare a laturii k este:
unde semnele 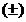 arata ca
poate fi utilizata fie conventia de la receptoare, fie cea de la
generatoare (evident - cu conditia ca latura sa fie rec. sau gen.).
arata ca
poate fi utilizata fie conventia de la receptoare, fie cea de la
generatoare (evident - cu conditia ca latura sa fie rec. sau gen.).
Din relatia de mai sus curentul 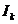 rezulta sub
forma:
rezulta sub
forma:
Se noteaza cu 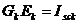 curentul de
scurtcircuit al laturii k, avand
semnul (+) cand iese dintr-un nod al laturii (nodul b) si cu (-) cand intra (nodul c),
curentul de
scurtcircuit al laturii k, avand
semnul (+) cand iese dintr-un nod al laturii (nodul b) si cu (-) cand intra (nodul c), 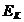 si
si 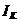 avand acelasi
sens prin latura k; in caz contrar
semnele de mai sus se inverseaza. Ca urmare:
avand acelasi
sens prin latura k; in caz contrar
semnele de mai sus se inverseaza. Ca urmare:
Inlocuind pe
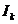 in ecuatia
corespunzatoare primei teoreme a lui Kirchhoff, se poate scrie:
in ecuatia
corespunzatoare primei teoreme a lui Kirchhoff, se poate scrie:
de unde:
Tensiunea 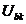 , la bornele laturii k,
este data de diferenta de preferential dintre cele doua
noduri, b si c:
, la bornele laturii k,
este data de diferenta de preferential dintre cele doua
noduri, b si c:
relatie ce poate fi folosita ca o schimbare
de variabila, astfel incat sistemul sa se reduca la (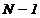 ) necunoscute, care sunt potentialele nodurilor independente.
) necunoscute, care sunt potentialele nodurilor independente.
Este necesar insa ca schimbarea de variabila
sa fie compatibila cu sistemul de ecuatii al teoremelor lui Kirchhoff.
Astfel, se constata ca cele O ecuatii date de teorema a II-a
sunt identic satisfacute de relatia 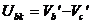 , deoarece fiecare potential de nod intra in
aceasta relatie de doua ori: intai cu (+), cand latura iese din nod si apoi cu (-), cand
latura intra in nod. Ca atare:
, deoarece fiecare potential de nod intra in
aceasta relatie de doua ori: intai cu (+), cand latura iese din nod si apoi cu (-), cand
latura intra in nod. Ca atare:
|
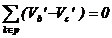 , respectiv , respectiv 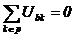
|
|
Rezulta ca cele (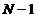 ) variabile cautate (potentialele de noduri) vor fi
univoc determinate de cele (
) variabile cautate (potentialele de noduri) vor fi
univoc determinate de cele (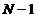 ) ecuatii ramase, date de teorema I.
) ecuatii ramase, date de teorema I.
In aceste conditii, sistemul de ecuatii
(4.4.56) devine:
luand, de
exemplu, ecuatia laturii dupa conventia de la receptoare.
Ordonand dupa potentialele nodurilor,
relatia (4.4.57) se mai poate scrie sub forma:
|
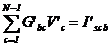 , , 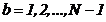
|
|
unde:
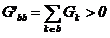 este conductanta
proprie a nodului b, egala cu
suma aritmetica a conductantelor laturilor concurente in nodul b;
este conductanta
proprie a nodului b, egala cu
suma aritmetica a conductantelor laturilor concurente in nodul b;
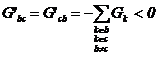 este conductanta
de cuplaj,dintre nodurile b si c, egala cu suma, luata cu semn schimbat, o
conductantelor laturilor care leaga nemijlocit (direct) cele
doua noduri, b si c.
este conductanta
de cuplaj,dintre nodurile b si c, egala cu suma, luata cu semn schimbat, o
conductantelor laturilor care leaga nemijlocit (direct) cele
doua noduri, b si c.
Daca cele doua noduri nu sunt unite
nemijlocit, atunci 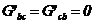 ;
;
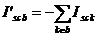 este curentul de scurtcircuit injectat in nodul b, format din suma algebrica a
curentilor de scurtcircuit ai laturilor active,
este curentul de scurtcircuit injectat in nodul b, format din suma algebrica a
curentilor de scurtcircuit ai laturilor active, 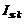 , legate la nodul b,
luata cu semnul schimbat; in aceasta relatie
, legate la nodul b,
luata cu semnul schimbat; in aceasta relatie 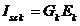 .
.
Dezvoltat,
sistemul (4.4.58) se scrie sub forma:
Algoritmul de aplicare a metodei
este urmatorul:
Se aleg nodurile independente (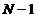 ) si nodul de referinta, N, pentru care se scriu ecuatiile potentialelor de
noduri.
) si nodul de referinta, N, pentru care se scriu ecuatiile potentialelor de
noduri.
Se calculeaza conductantele
laturilor (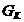 ).
).
Se calculeaza conductantele proprii
si de cuplaj si curentii de scurtcircuit injectati in
noduri (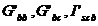 ).
).
Se scrie sistemul de ecuatii al
potentialelor si se rezolva in raport cu acestea.
Se calculeaza tensiunile la bornele
laturilor:
Se calculeaza curentii din laturi,
pornind de la ecuatiile laturilor. De exemplu, in cazul utilizarii
conventiei de la receptoare se poate scrie:
sau:
unde 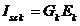 este, cum s-a
aratat, curentul de scurtcircuit al laturii k.
este, cum s-a
aratat, curentul de scurtcircuit al laturii k.
Se face verificarea rezultatelor, de exemplu,
cu ajutorul teoremei bilantului puterilor.
Nota
Curentul de scurtcircuit al unei
laturi (active), 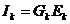 , nu trebuie confundat cu cel de scurtcircuit al unui nod al
retelei, la care este conectata latura respectiva:
, nu trebuie confundat cu cel de scurtcircuit al unui nod al
retelei, la care este conectata latura respectiva: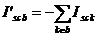 , acesta din urma fiind constituit, asa cum s-a
aratat, din suma algebrica a curentilor de scurtcircuit ai
laturilor active, legate la nodul (b), luata cu semn schimbat.
, acesta din urma fiind constituit, asa cum s-a
aratat, din suma algebrica a curentilor de scurtcircuit ai
laturilor active, legate la nodul (b), luata cu semn schimbat.
Aplicatie
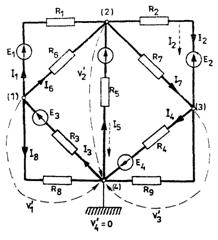
Se
da reteaua liniara de c.c. din figura (4.4.20), pentru care se
cunosc:
Sa
se calculeze curentii cu ajutorul metodei potentialelor de noduri
si sa se verifice rezultatele.
Rezolvare
Se
alege arbitrar nodul (4) ca referinta
(V4 = 0), respectiv se
considera acesta legat la pamant.
Se calculeaza conductantele proprii
si de cuplaj ale laturilor si curentii de scurtcircuit din
nodurile retelei:
Curentii de scurtcircuit injectati in noduri
sunt:
Se scrie sistemul de ecuatii in potentiale
si se rezolva:
Inlocuind valorile conductantelor si
curentilor se obtine:
de unde:
Se calculeaza curentii din laturi:
Curentul 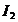 va avea sensul opus
celui ales arbitrar (initial), respectiv sensul sagetii punctate.
va avea sensul opus
celui ales arbitrar (initial), respectiv sensul sagetii punctate.
Curentul 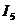 va avea, de asemenea,
sens opus celui ales initial, motiv pentru care i se va schimba sensul pe
schema electrica (sageata punctata). Se vede ca in acest
caz curentul nu va mai avea acelasi sens cu
va avea, de asemenea,
sens opus celui ales initial, motiv pentru care i se va schimba sensul pe
schema electrica (sageata punctata). Se vede ca in acest
caz curentul nu va mai avea acelasi sens cu 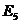 , deci sursa
, deci sursa 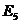 se incarca,
respectiv absoarbe energie din retea.
se incarca,
respectiv absoarbe energie din retea.
Verificare:
Se vede ca: 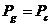 .
.
Nota
La
calculul lui 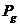 termenul
termenul 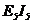 se scade, deoarece
sursa
se scade, deoarece
sursa 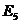 , asa cum s-a aratat, absoarbe energie de la
retea in loc sa-i cedeze energie acesteia (are semnul opus lui
, asa cum s-a aratat, absoarbe energie de la
retea in loc sa-i cedeze energie acesteia (are semnul opus lui 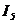 )
)



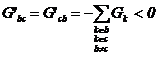 este conductanta
de cuplaj,dintre nodurile b si c, egala cu suma, luata cu semn schimbat, o
conductantelor laturilor care leaga nemijlocit (direct) cele
doua noduri, b si c.
este conductanta
de cuplaj,dintre nodurile b si c, egala cu suma, luata cu semn schimbat, o
conductantelor laturilor care leaga nemijlocit (direct) cele
doua noduri, b si c.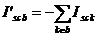 este curentul de scurtcircuit injectat in nodul b, format din suma algebrica a
curentilor de scurtcircuit ai laturilor active,
este curentul de scurtcircuit injectat in nodul b, format din suma algebrica a
curentilor de scurtcircuit ai laturilor active,