Optimizari dinamice
Optimizarea regimurilor dinamice a fost
caracteristica atumaticii inca de la inceputurile aplicatiilor practice ale
acesteia, intrucat intr-o forma sau alta proiectarea unui sistem automat
trebuie sa includa anumite elemente de optimizare a regimurilor tranzitorii, in
caz contrar existand pericolul ca functionarea sistemului sa fie
necorespunzatoare si ca urmare sa rezulte o calitate nesatisfacatoare a
produselor obtinute din instalatia tehnologica automatizata, o uzura accelerata
a acestei instalatii sau o exploatare nerationala etc.
Dupa cum se stie, in cazul sistemelor de
reglare automata regimurile tranzitorii (care pot fi denumite si regimuri
dinamice) sunt provocate de variatiile marimii de intrare a sistemului - numita
si marime de referinta - sau de variatiile unor perturbari [3, 4].
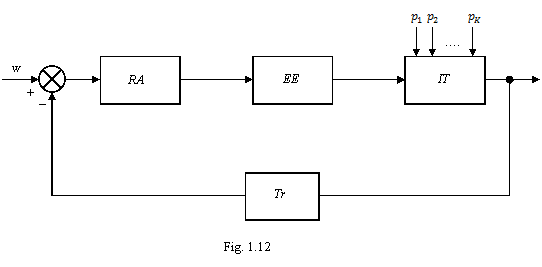
In cazul cel mai simplu al unui sistem de
reglare automata in functie de iesire, monovariabil (cu o singura marime de
referinta 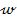 si o
singura marime reglata), liniar si continuu, schema de elemente are aspectul
din figura 1.12, unde RA este
regulatorul automat, EE - elementul
de executie, IT - instalatia
tehnologica, Tr - traductorul,
si o
singura marime reglata), liniar si continuu, schema de elemente are aspectul
din figura 1.12, unde RA este
regulatorul automat, EE - elementul
de executie, IT - instalatia
tehnologica, Tr - traductorul, 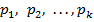 -
perurbarile care actioneaza asupra insalatiei tehnologice.
-
perurbarile care actioneaza asupra insalatiei tehnologice.
Sistemele de reglarein functie de iesire
au fost primele folosite in practica industriala si se utilizeaza cu succes
teoria reglarii in functie de stare [3, 4].
Grupand elementele EE, IT si Tr intr-un singur bloc echivalent F rezulta pentru schema de elemente
aspectul din figura 1.13, unde F este
blocul echivalent al partii fixate a sistemului ("fixate" in sensul ca pentru a
influenta performantele sistemului proiectantul automatizarii are foarte putine
posibilitati de a modifica parametri din blocul F, in raport cu posibilitatile de a alege structura si parametrii
regulatorului automat), ε - eroarea, u - marimea de comanda, y
- marimea reglata, respectiv marimea de iesire a sistemului, iar RA, 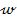
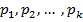 au aceleasi
semnificatii ca in figura 1.12.
au aceleasi
semnificatii ca in figura 1.12.
Regimul tranzitoriu al marimii reglate y, provocat de o variatie treapta
unitara a marimii de referinta 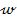 , are aspectul din figura 1.14 (in ipoteza ca in
regim stationar
, are aspectul din figura 1.14 (in ipoteza ca in
regim stationar 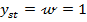 , deci in ipoteza unei valori nule a erorii
stationare
, deci in ipoteza unei valori nule a erorii
stationare 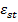 , intrucat - conform figurii 1.13 -
, intrucat - conform figurii 1.13 - 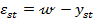 , deci
, deci 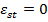 ), iar regimul tranzitoriu provocat de o variatie
treapta a unei perturbari are aspectul din figura 1.15, in aceeasi ipoteza.
), iar regimul tranzitoriu provocat de o variatie
treapta a unei perturbari are aspectul din figura 1.15, in aceeasi ipoteza.
Considerand schema din figura 1.13, din
care se obtine
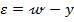 (1.3)
(1.3)
rezulta ca din
curbele din figurile 1.14 si 1.15 se obtin aspectele variatiilor in timp
corespunzatoare ale erorii ε din figurile 1.16 si 1.17.
In cazul raspunsului la variatia treapta
unitara pozitiva a marimii de referinta 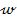 (fig. 1.14)
regimul tranzitoriu indeal al marimii reglate y ar fi cel in care marimea reglata ar urmari fidel - si deci
instantaneu - variatia marimii de referinta, deci pentru marimea y ar rezulta tot o treapta unitara
pozitiva; ca urmare din figurile 1.14 si 1.16 rezulta ca aria delimitata de
curba ε din figura 1.16
ar trebui sa tinda catre zero.
(fig. 1.14)
regimul tranzitoriu indeal al marimii reglate y ar fi cel in care marimea reglata ar urmari fidel - si deci
instantaneu - variatia marimii de referinta, deci pentru marimea y ar rezulta tot o treapta unitara
pozitiva; ca urmare din figurile 1.14 si 1.16 rezulta ca aria delimitata de
curba ε din figura 1.16
ar trebui sa tinda catre zero.
O asemenea comportare ideala nu este
posibila, intrucat transmiterea variatiei marimii de referinta spre iesirea
sistemului se efectueaza cu anumite intarzieri inerente cu cat insa aria
mentionata anterior va fi mai mica, cu atat regimul tranzitoriu se va apropia
de cel ideal. Acest considerent a condus la ideea alegerii unui criteriu de
optimizare dinamica legat de minimizarea ariei respective.


Valoarea ariei este definita de integrala
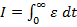 (1.4)
(1.4)
dar aceasta
expresie nu poate fi folosita in calitate de criteriu, deoarece ordonatele
marimii ε pot interveni
cu semne diferite si deci o valoare redusa pentru I nu atesta prezenta unui regim tranzitoriu de calitate buna.
Acest inconvenient poate fi eliminat pe
mai multe cai. Cea mai simpla consta in adoptarea unui criteriu de optimizare
de forma
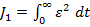 (1.5)
(1.5)
minimizarea
acestui criteriu integral patratic asigurand un optim pentru regimul
tranzitoriu in sensul obtinerii unei anumite apropieri dorite de regimul ideal.
In cazul raspunsului la perturbare (fig.
1.15) regimul tranzitoriu ideal ar fi cel in care marimea reglata y nu ar fi
deloc influientata, pastrandu-si neschimbata valoarea anterioara variatiei
perturbarii p. Ca urmare, dupa cum
rezulta din figurile 1.15 si 1.17, se constata ca si in acest caz regimul
tranzitoriu va fi cu atat mai apropiat de cel ideal, cu cat va fi mai mica aria
delimitata de curba ε
din figura 1.17.
In consecinta raman valabile
considerentele care au condus la expresia unui criteriu de optimizare de forma
(1.5), deci la adoptarea criteriilor integrale patratice.
Minimizarea criteriilor integrale
mentionate conduce la valori optime ale parametrilor regulatorului automat,
care asigura un indice sintetic de calitate a regimului tranzitoriu, in sensul
ca nu pot asigura anumite performante specificate separat pentru acest regim,
cum ar fi valoarea suprareglakului 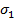 (figurile
1.14 si 1.16), valoarea abaterii maxime
(figurile
1.14 si 1.16), valoarea abaterii maxime 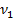 (figurile
1.15 si 1.17), amortizarea oscilatiilor - definita de rapoartele
(figurile
1.15 si 1.17), amortizarea oscilatiilor - definita de rapoartele 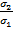 sau
sau 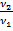 - sau
durata regimului tranzitoriu.
- sau
durata regimului tranzitoriu.
Pentru obtinerea unei asemenea
performante specificate separat pot fi alese criterii de optimizare de alta
forma, de exemplu de forma
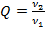 (1.6)
(1.6)
minimizarea
acestui criteriu conduce la parametrii regulatorului care asigura cea mai buna
amortizare a oscilatiilor.
In multe cazuri criteriile integrale
patratice au un obiectiv combinat, urmand nu numai optimizarea regimului
tranzitoriu, ci o optimizare care reprezinta un compromis intre atingerea
primului obiectiv (calitate buna a regimului tranzitoriu) si a celui de al
doilea obiectiv; de cele mai multe ori in practica acest al doilea obiectiv
vizeaza reducerea consumului de energie pentru realizarea actiunii de reglare
automata, respectiv pentru comanda deplasarii elementului de executie.
Reducerea acestui consum poate fi obtinuta prin adoptarea unui criteriu
integral patratic de forma
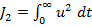 (1.7)
(1.7)
- unde u
este marimea de comanda de la iesirea regulatorului automat RA (fig. 1.13) - intrucat marimea u este un curent electric sau o
tensiune, cum este cazul regulatoarelor electrice.
Compromisul intre obiectivele referitoare
la regimul tranzitoriu si la consumul de energie se realizeaza usor, adoptand
un criteriu combinat, de forma
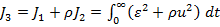 (1.8)
(1.8)
unde ρ este un factor de ponderare.
Expresia (1.8) ilustreaza unul din cele mai simple cazuri de optimizare
dupa mai multe criterii, denumita "polioptimizare".
In stadiul actual de dezvoltare a
instalatiilor tehnologice, care au atins un grad de complexitate foarte
ridicat, necesitatea polioptimizarii intervine intr-un numar din ce in ce mai
mare de probleme de optimizare.
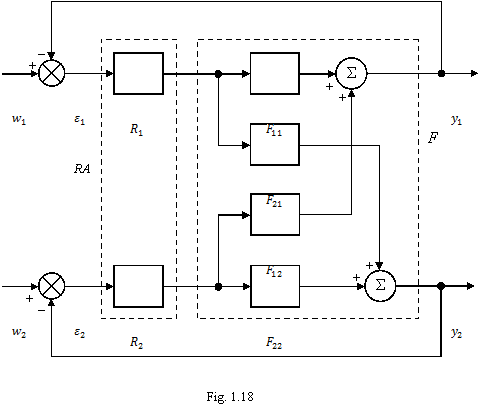
Un exemplu imediat poate fi oferit de un
sistem de reglare automata multivariabil, cu doua marimi de referinta  si
si  si cu doua
marimi reglate
si cu doua
marimi reglate 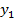 si
si 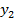 , avand schema din figura 1.18. In cadrul
regulatorului automat intervin blocurile
, avand schema din figura 1.18. In cadrul
regulatorului automat intervin blocurile 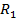 si
si 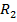 , care primesc erorile
, care primesc erorile 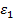 si
si 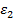 ale celor
doua bucle, iar in cadrul partii fixate F
intervin blocurile
ale celor
doua bucle, iar in cadrul partii fixate F
intervin blocurile 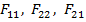 si
si 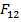 , ultimile doua reprezentand caile de transmiterea
actiunilor de interinfluienta [16].
, ultimile doua reprezentand caile de transmiterea
actiunilor de interinfluienta [16].
Se constata ca in calitate de criteriu
integral patratic pentru optimizare poate fi folosita expresia
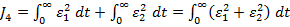 (1.9)
(1.9)
In multe cazuri, in criteriile integrale
patratice pentru optimizarea regimurilor tranzitorii intervin si derivate ale
erorii [3, 4].
Criteriile integrale patratice se
formuleaza si in limbajul intrare-stare-iesire, care descrie functionarea
sistemului prin intermediul ecuatiilor de stare.
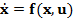 (1.10)
(1.10)
unde x este vectorul starilor, iar u este de regula vectorul comenzilor
dar poate defini si un set de parametri [22].
Exemple care ilustreaza formularea criteriilor integrale in limbaj
intrare-stare-iesire sunt reprezentate de expresiile
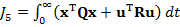 (1.11)
(1.11)
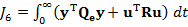 (1.12)
(1.12)
unde x, u, y sunt
vectorii starilor, comenzilor si marimilor de iesire (reglate); 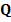
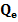 , R -
matrice de ponderare.
, R -
matrice de ponderare.
Aspectul criteriilor integrale
prezentate anterior rezulta din doua ipoteze prealabile, Prima, pusa in
evidenta de figurile 1.14 . 1.17 consta in considerarea conditiei de
eroare stationara nula.
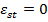 (1.13)
(1.13)
iar a doua - rezultand din expresiile (1.5), (1.7), (1.8),
(1.9), (1,11) - consta in faptul ca nu se impune la un moment final 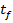 si ca urmare acest moment reprezinta limita
superioara a operatiei de integrare, iar uneori se impune si o anumita valoare
a variabilelor pentru momentul
si ca urmare acest moment reprezinta limita
superioara a operatiei de integrare, iar uneori se impune si o anumita valoare
a variabilelor pentru momentul 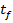 . Astfel, pentru ilustrare, se
considera un motor electric - comandat prin intermediul tensiunii de excitatie
- si se urmareste gasirea comenzii optime u
(reprezentand tensiunea aplicata circuitului de excitatie) pentru ca sa rezulte
o variatie cat mai apropiata de o treapta, a pozitiei unghiulare θ a
arborelui de la o valoare initiala considerata 0 radiani la o valoare finala de
10 radiani, impunandu-se un timp final
. Astfel, pentru ilustrare, se
considera un motor electric - comandat prin intermediul tensiunii de excitatie
- si se urmareste gasirea comenzii optime u
(reprezentand tensiunea aplicata circuitului de excitatie) pentru ca sa rezulte
o variatie cat mai apropiata de o treapta, a pozitiei unghiulare θ a
arborelui de la o valoare initiala considerata 0 radiani la o valoare finala de
10 radiani, impunandu-se un timp final 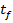 si deci o valoare finala
si deci o valoare finala 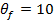 rad [22].
rad [22].
Pentru obtinerea
comenzii optime se poate filosi in acest caz un criteriu integral de forma
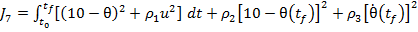 (1.14)
(1.14)
unde
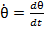
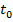 - momentul initial, cand are loc aplicarea
comenzii u;
- momentul initial, cand are loc aplicarea
comenzii u;
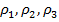 - factori de ponderare.
- factori de ponderare.
Primul termen al
sumei din (1.14) prezinta analogii cu expresia (1.8), intrucat
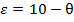 (1.15)
(1.15)
valoarea de 10
radiani fiind valoarea prescrisa pentru variatia pozitiei unghiulare θ
Introducerea celui de-al doilea termen
are ca obiectiv sa asigure si o minimizare a diferentei dintre pozitia
unghiulara finala 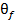 - la care
se va ajunge efectiv - si pozitia finala prescrisa, de 10 radiani; folosirea
patratului diferentei din al doilea tremen are acelasi scop cu folosirea la
patrat a integranzilor din primul termen, respectiv de a elimina efectele
nedorite ale variatiei semnului diferentei mentionate.
- la care
se va ajunge efectiv - si pozitia finala prescrisa, de 10 radiani; folosirea
patratului diferentei din al doilea tremen are acelasi scop cu folosirea la
patrat a integranzilor din primul termen, respectiv de a elimina efectele
nedorite ale variatiei semnului diferentei mentionate.
In al treilea termen intervine patratul
valorii derivatei 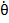 la monentul
final
la monentul
final 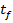 ; daca regimul tranzitoriu se incheie pana la
acest moment final impus, atunci pozitia unghiulara
; daca regimul tranzitoriu se incheie pana la
acest moment final impus, atunci pozitia unghiulara 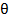 ajunge la
valoarea constanta de 10 radiani si deci
ajunge la
valoarea constanta de 10 radiani si deci
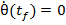 (1.16)
(1.16)
Introducerea
celui de-al treilea termen in expresia (1.14) are ca obiectiv sa asigure si o
minimizare a valorii derivatei 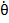 la momentul
final
la momentul
final 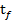 , pentru acest moment fiind prescrisa o valoare
nula a derivatei respective.
, pentru acest moment fiind prescrisa o valoare
nula a derivatei respective.
Folosirea unui criteriu integral de tipul
(1.14) permite nu numai obtinerea unui regim tranzitoriu de buna calitate -
prin termenul integral din (1.14) - ci si obtinerea unei comportari bune la
intrarea in noul regim stationar, prin intermediul celorlalti doi termeni din (1.14).
Aplicarea puternicei metode de optimizare
pe care o reprezinta criteriile integrale este tratata in capitolele urmatoare
pentru sistemele liniare.