Optimizari stationare
In foarte multe domenii industriale se
pune problema determinarii anumitor valori optime ale unor marimi si a
mentinerii acestor valori pe perioade de timp relativ indelungate, fara ca in
cadrul acestei probleme sa fie oportuna si studierea caracteristicilor unor
regimuri tranzitorii care apar la eventuale modificari ale valorilor marimilor
mentionate.
Asemenea optimizari, care au ca scop
determinarea valorilor stationare optime pentru anumite marimi sunt denumite
optimizari ale regimurilor stationare sau optimizari stationare (uneori se
foloseste si denumirea "optimizari statice" [20] ).
In unele cazuri valorile stationare
optime sunt determinate prin intermediul unor calculatoare care nu sunt conectate la procesele tehnologice si
la echipamentele de reglare automata aferente (calculatoarele "off-line"),
operatorul uman luand masuri pentru aducerea marimilor respective la valorile
optime, de regula prin fixarea acestor valori pentru semnalele de referinta ale
unor bucle de reglare. In alte cazuri, calculatorul care determina valorile
optime realizeaza o conducere in regim de supraveghere a procesului de
tehnologic [4], primind direct de la proces o serie de marimi masurate si
asigurand stabilirea valorilor optime pentru semnalele de referinta ale
buclelor de reglare mentionate.
Evident, in fiecare bucla de reglare vor
exista regimuri tranzitorii, provocate de modificarea valorii semnalelor de referintasau de actiunea unor perturbari,
dar optimizarea acestor regimuri constituie o problema locala a fiecarei bucle,
separata de problema de ansamblu a optimizarii regimurilor stationare.
Importanta optimizarii stationare si a
efectelor economice pe care le realizeaza poate fi pusa in evidenta prin
numeroase exemple din diferite domenii industriale. In figura 1.11 este
prezentat un exemplu de instalatie tehnologica din industria chimica [21], care
ilustreaza aspectele problemelor de optimizare a regimurilor stationare.
 Instalatia include reactorul R,
schimbatorul de caldura S, decantorul
D si coloana de distilare C. In reactorul R, prevazut cu paleta de amestecare PA, intra reactantii A si
B - cu debitele
Instalatia include reactorul R,
schimbatorul de caldura S, decantorul
D si coloana de distilare C. In reactorul R, prevazut cu paleta de amestecare PA, intra reactantii A si
B - cu debitele 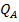 si
si  - precum si
debitul
- precum si
debitul 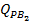 , reprezentand fractiunea recirculata prin reactor
din debitul total
, reprezentand fractiunea recirculata prin reactor
din debitul total  de produs
de baza al coloanei; restul produsului de baza, respectiv debitul
de produs
de baza al coloanei; restul produsului de baza, respectiv debitul  , este folosit in calitate de combustibil.
, este folosit in calitate de combustibil.
Din reactorul R, in care temperatura are valoarea T, se obtine debitul total 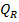 , care insumeaza debitele a 6 componente rezultate
din reactile: debitele
, care insumeaza debitele a 6 componente rezultate
din reactile: debitele  si
si 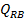 , corespunzatoare cantitatiilor din reactantii A si B
care nu au participat la reactie, debitele
, corespunzatoare cantitatiilor din reactantii A si B
care nu au participat la reactie, debitele 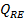 si
si  ale
produselor secundare E si F obtinute din reactie, debitul
ale
produselor secundare E si F obtinute din reactie, debitul 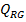 de produs
secundar greu, uleios, G, obtinut din
reactie si debitul
de produs
secundar greu, uleios, G, obtinut din
reactie si debitul 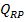 de produs
principal.
de produs
principal.
Debitul total 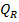 de iesire
din reactor intra in schimbatorul de caldura S (in care are loc un proces de racire datorita fluidului de racire
FR), trecand apoi in decantorul D, care separa produsul greu G, la baza decantorului rezultand
debitul
de iesire
din reactor intra in schimbatorul de caldura S (in care are loc un proces de racire datorita fluidului de racire
FR), trecand apoi in decantorul D, care separa produsul greu G, la baza decantorului rezultand
debitul 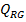 ; produsul greu G nu poate fi utilizat si in plus necesita o anumita tratare - deci
implica o anumita cheltuiala - inainte de a fi evacuat ca reziduu,
evitandu-se astfel efectele de poluare
provocate de produsul respectiv.
; produsul greu G nu poate fi utilizat si in plus necesita o anumita tratare - deci
implica o anumita cheltuiala - inainte de a fi evacuat ca reziduu,
evitandu-se astfel efectele de poluare
provocate de produsul respectiv.
Produsele intermediare E si F
pot fi folosite numai in calitate de combustibili si au deci o valoare utila
corespunzatoarel folosirea debitului  - o parte din debitul
- o parte din debitul  de produs
de baza al coloanei C - in calitate
de combustibil este posibila datorita acestei proprietati utile a produselor
intermediare E si F.
de produs
de baza al coloanei C - in calitate
de combustibil este posibila datorita acestei proprietati utile a produselor
intermediare E si F.
Dupa separarea produsului greu G, in decantor, restul componentelor
debitului 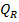 intra in
coloana C, din care se obtine la varf
produsul principal P, cu debitul
intra in
coloana C, din care se obtine la varf
produsul principal P, cu debitul 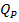 , iar la baza rezulta debitul de produs de baza PB, cu debitul
, iar la baza rezulta debitul de produs de baza PB, cu debitul  , impartit in debitul de combustibil
, impartit in debitul de combustibil  si debitul de recirculare in reactor
si debitul de recirculare in reactor 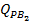
Functionarea instalatiei tehnologice este
caracterizata de 12 marimi: debitele 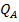

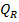
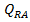
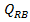
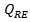


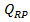

 si
temperatura din reactor T; aceste
marimi intervin atat in expresia criteriului de optimizare, cat si in
expresiile restrictiilor.
si
temperatura din reactor T; aceste
marimi intervin atat in expresia criteriului de optimizare, cat si in
expresiile restrictiilor.
Optimizarea stationara are ca obiectiv sa
determine pentru instalatia tehnologica acel regim de functionare de lunga
durata - respectiv acele valori stationare optime ale marimilor caracterizand
functionarea instalatiei - care sa asigure maximizarea ratei anuale de
recuperare a investitiilor, in ipoteza unui anumit numar de ore de functionare
pe an (de exemplu, 8400 ore/an).
Expresia criteriului de optimizare -
respectiv a ratei anuale de recuperare a investitiilor - se obtine in functie
de unele din cele 12 marimi mentionate anterior [21]. Prin intermediul
deferitelor grupe de marimie se obtin expresiile restrictiilor de tip egalitate
(9 restrictii).
Restrictiile de tip egalitate rezulta
scriind ecuatiile bilanturilor de material pe ansamblu si pentru fiecare
componenta. De exemplu, pentru ansamblul instalatiei tehnologice rezulta
relatia de egalitate a debitelor de intrare si de iesire:
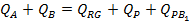 (1.1)
(1.1)
deci se obtine
relatia de tip egalitate
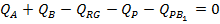 (1.2)
(1.2)
Restrictiile de tip inegalitate rezulta
din admisibilitatea unei game limitate (superior si inferior) pentru
temperatura T din reactorul R, din limitarea debitului de produs
principal 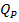 care poate
fi obtinut de instalatie si din conditiile de pozitivitate a debitelor
diferitelor componente.
care poate
fi obtinut de instalatie si din conditiile de pozitivitate a debitelor
diferitelor componente.
Dupa cum se constata din exemplul
considerat, optimizarea stationara isi propune ca obiectiv determinarea
valorilor stationare optime ale unor marimi, care vor fi mentinute timp
indelungat pentru obtinerea unui maxim al criteriului, reprezentat de rata
anuala de recuperare a investitiilor, insasi criteriul fiind formulat prin
intermediul unui interval mare de timp.
Mentinerea anumitor marimi la valorile
optime stabilite se va face prin intermediul unor bucle locale de reglare
automata in care vor interveni regimuri tranzitorii, dar eventuala optimizare a
acestor regimuri formeaza obiectul unei alte clase de probleme: problemele de
optimizare dinamica.
Exemplul analizat pune in evidenta
importantele efecte economice care pot rezulta prin intermediul optimizarilor stationare.


