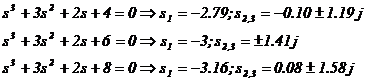Stabilitatea
BIBO a sistemelor dinamice liniare
Obiectiv:
Explicarea notiunii de sistem dinamic liniar BIBO stabil. Prezentarea
teoremelor si criteriilor ce permit analiza BIBO stabilitatii
sistemelor dinamice liniare.
1. Breviar
teoretic
Definitii
1. Un sistem dinamic liniar se numeste BIBO stabil
daca si numai daca raspunsul acestui sistem, la orice
semnal de intrare marginit, este marginit.
2. Un sistem dinamic liniar se numeste instabil BIBO
daca exista un semnal de intrare marginita pentru care
raspunsul sistemului este nemarginit.
Teoreme de caracterizare a BIBO stabilitatii
T1. Un sistem dinamic liniar este BIBO
stabil daca si numai daca toti polii sistemului au partea
reala strict negativa
Exemple:
a)
Fie sistemul dinamic liniar descris de functia de transfer:
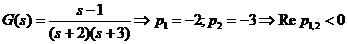
Sistemul
este BIBO stabil.
b) Fie sistemul dinamic liniar descris de
functia de transfer:
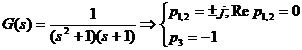
Sistemul
este instabil BIBO.
T2. Un sistem dinamic liniar este BIBO
stabil daca si numai daca raspunsul indicial al sistemului
tinde catre o valoare constanta (numita valoare de regim
permanent/stationar):
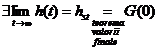
Exemple:
a)
Fie:
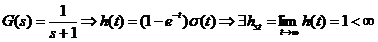
Sistemul
este BIBO stabil.
b)
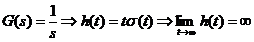
Sistemul
este instabil BIBO.
T3. Un sistem dinamic liniar este BIBO
stabil daca si numai daca :
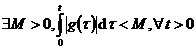
Exemple:
a) Fie:
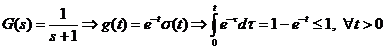
Sistemul este BIBO stabil.
b)
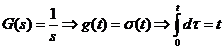
Sistemul este instabil BIBO.
T4. Daca un sistem dinamic liniar
este BIBO stabil atunci toti coeficientii din polinomul polilor sunt
strict pozitivi. Daca cel putin un coeficient din polinomul polilor
este zero sau strict negativ sistemul este instabil BIBO.
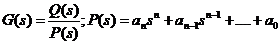 ,
, 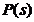 = polinomul polilor.
= polinomul polilor.
Daca 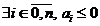 , atunci sistemul este instabil BIBO. Daca toti
coeficientii lui P(s) sunt
strict pozitivi nu se poate preciza nimic, pe baza acestei teoreme, despre BIBO
stabilitatea sistemului.
, atunci sistemul este instabil BIBO. Daca toti
coeficientii lui P(s) sunt
strict pozitivi nu se poate preciza nimic, pe baza acestei teoreme, despre BIBO
stabilitatea sistemului.
Exemple:
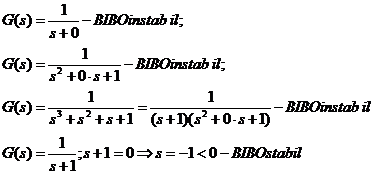
Criterii polinomiale de analiza a BIBO
stabilitatii
Daca polinomul polilor este de grad mare
si/sau coeficientii lui sunt dependenti de parametri reali este
dificila aplicarea teroremelor de mai sus pentru a studia BIBO
stabilitatea sistemelor dinamice liniare.
Se recomanda in aceste situatii
aplicarea unuia din urmatoarele criterii polinomiale:
C1. Criteriul Hurwitz:
Fie
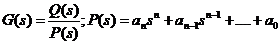 ,
, 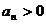 .
.
Se construieste matricea Hurwitz:
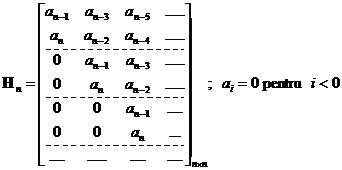
Polinomul P(s) este hurwitzian (admite doar
radacini cu parte reala strict negativa) si deci sistemul
G(s) este BIBO stabil daca toti minorii principali diagonali ai
matricii H sunt strict pozitivi.
Observatii
Se poate
considera ca matrice Hurwitz transpusa lui Hn anterior indicat, avand
in vedere ca minorii principali diagonali rezulta aceiasi.
Polinomul 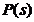 poate fi adus la forma
monica
poate fi adus la forma
monica 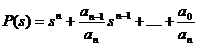 , garantand astfel indeplinirea conditiei care
solicita ca
, garantand astfel indeplinirea conditiei care
solicita ca 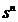 sa aiba
coeficient pozitiv.
sa aiba
coeficient pozitiv.
Exemplu:
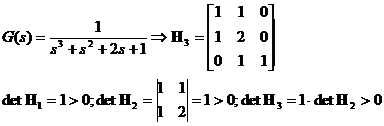
Sistemul
este BIBO stabil.
C2. Criteriul Routh:
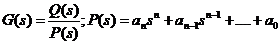 ,
, 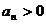 .
.
Se completeaza schema Routh
dupa urmatorul algoritm:

Ultima linie din schema Routh va contine un singur
element.
Polinomul P(s) este hurwitzian (sistemul G(s) BIBO stabil)
daca si numai daca toate elementele din prima coloana a
schemei Routh sunt strict pozitive.
Observatie:
Polinomul 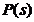 poate fi adus la forma
monica
poate fi adus la forma
monica 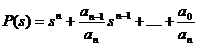 , garantand astfel indeplinirea conditiei care
solicita ca
, garantand astfel indeplinirea conditiei care
solicita ca 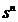 sa aiba
coeficient pozitiv.
sa aiba
coeficient pozitiv.
Exemplu:
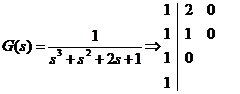 - Sistem BIBO stabil
- Sistem BIBO stabil
2.Exercitii
rezolvate (analitic)
Exercitiul 1 Fie circuitul electric din fig.1. Se
considera: 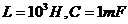 .
.
Studiati BIBO
stabilitatea sistemului.
Solutie: Acest circuit este modelat prin urmatoarea functie de
transfer:
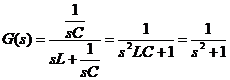
Polii sistemului sunt: 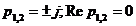
Sistemul este instabil BIBO.
Aceasta proprietate poate fi
evidentiata experimental urmarind raspunsul sistemului la
un semnal de intrare marginit:
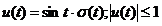
Se obtine:
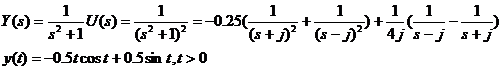
|
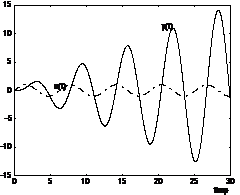
Fig. 2
|
Raspunsul sistemului este
nemarginit, desi intrarea aplicata sistemului este
marginita (vezi fig.2)
Exercitiul 2 Fie sistemul dinamic liniar descris de functia
de transfer:
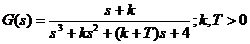
Gasiti valorile
parametrilor reali k si T pentru care sistemul este BIBO stabil.
Solutie: Se aplica criteriul Hurwitz. Matricea corespunzatoare
polinomului polilor este:
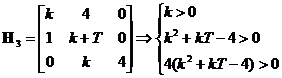
|

Fig. 3
|
Sistemul este BIBO stabil pentru:
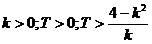
Pe baza tabloului de variatie de mai jos
se poate obtine in planul parametrilor k
si T domeniul de stabilitate
BIBO a sistemului (vezi fig. 3)
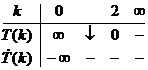
Se urmareste in continuare
comportarea sistemului pe raspuns indicial, in domeniul de BIBO
stabilitate, BIBO instabilitate si la limita de stabilitate.
a) in domeniul de BIBO stabilitate:
pentru 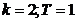 :
:
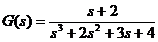
Polii sistemului sunt cu parte reala
negativa: 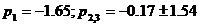 . Raspunsul indicial al sistemului trebuie sa
tinda (conform teoremei 1) la o valoare constanta de regim permanent:
. Raspunsul indicial al sistemului trebuie sa
tinda (conform teoremei 1) la o valoare constanta de regim permanent:
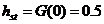 (vezi fig. 4a)
(vezi fig. 4a)
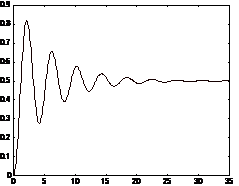

Fig.
4a Fig. 4b
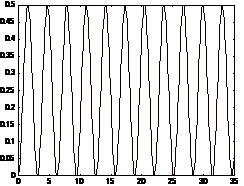
Fig. 4c
b) in domeniul de instabilitate BIBO
Se alege: 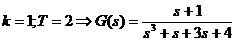
Raspunsul indicial al sistemului nu tinde
catre o valoare constanta.
Polii sistemului sunt: 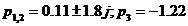
Doi poli au parte reala strict
pozitiva si raspunsul indicial al sistemului este
nemarginit (vezi fig. 4b).
c) la limita de stabilitate este
indeplinita una din conditiile:
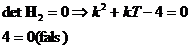
Se alege
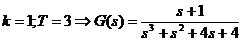
Polii sistemului sunt: 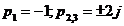
Doi poli complecsi au partea reala
nula. Sistemul este instabil BIBO si raspunsul indicial nu tinde
catre o valoare constanta (vezi fig. 4c). In aceasta
situatie, deoarece sistemul admite poli pur imaginari si polul real
este strict negativ, raspunsul indicial este marginit.
3. Analiza
stabilitatii BIBO in Matlab
BIBO stabilitatea sistemelor dinamice liniare poate fi
verificata in Matlab cu ajutorul teoremei T2, vizualizand graficul
raspunsului indicial, sau cu ajutorul teoremei T1, determinand polii
sistemului si urmarind semnul partii lor reale.
4. Probleme
propuse
Problema 1 Fie sistemul dinamic liniar descris de functia de
transfer:
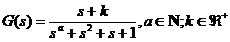
a) gasiti
valorile parametrului a pentru care
sistemul este BIBO stabil (indicatie: considerati cazurile
a>3; a=3; a=2; a=1; a=0).
b) determinati
in
domeniul de BIBO stabilitate valoarea de regim stationar a raspunsului
indicial.
c)
verficati
experimental rezulatul de la punctuele a), b).
Problema 2 Fie sistemul dinamic liniar descris de schema bloc din fig.
5, in
care T>0;K>0.
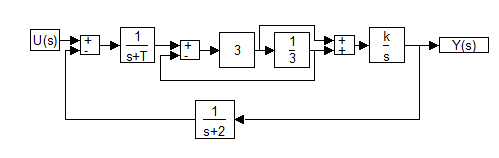 Fig. 5
Fig. 5
a) stiind ca
sistemul este descris prin functia de transfer echivalenta
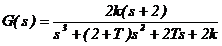
se cere sa
se studieze stabilitatea BIBO in planul parametrilor k >0 si T
>0; care este valoarea de regim stationar? (Atentie! valoarea de
regim stationar
poate fi calculata
doar in domeniul de BIBO stabilitate)
b) sa se obtina
(analitic si
prin simulare) raspunsul
indicial pentru:
Pentru rezolvarea analitica
sunt oferite rezultatele:
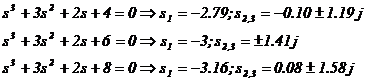


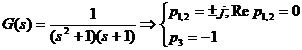
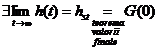
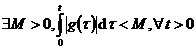
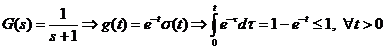
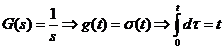
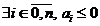 , atunci sistemul este instabil BIBO. Daca toti
coeficientii lui P(s) sunt
strict pozitivi nu se poate preciza nimic, pe baza acestei teoreme, despre BIBO
stabilitatea sistemului.
, atunci sistemul este instabil BIBO. Daca toti
coeficientii lui P(s) sunt
strict pozitivi nu se poate preciza nimic, pe baza acestei teoreme, despre BIBO
stabilitatea sistemului.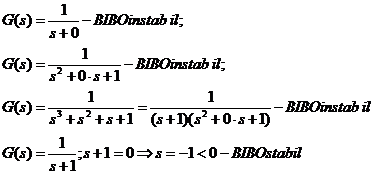
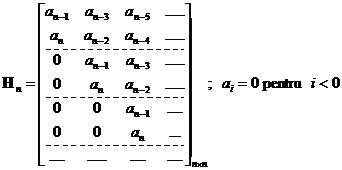
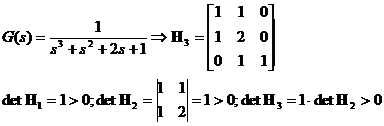

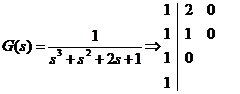 - Sistem BIBO stabil
- Sistem BIBO stabil
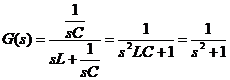
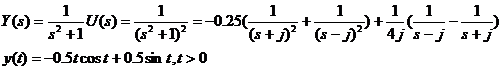
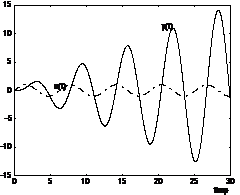
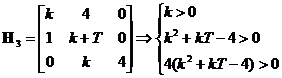

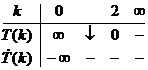



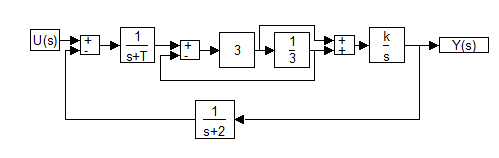 Fig. 5
Fig. 5