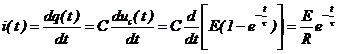Studiul incarcarii unui condensator

Studiul incarcarii unui condensator

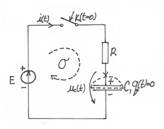
Fie un circuit de c.c. care contine o sursa de c.c., E, o rezistenta R si condensatorul C. Se va analiza procesul de incarcare al condensatorului, incepand din momentul inchiderii intrerupatorului K si alimentarii circuitului.

Ecuatia circuitului in momentul inchiderii intrerupatorului K(t=0) este:

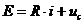Regimul de incarcare este un regim variabil (tranzitoriu), astfel ca marimile de stare, 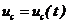si,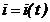, sunt variabile in timp pe intreaga durata a acestui proces.

Se aplica legea conservarii sarcinii electrice (pentru cazul incarcarii unui condensator):

care in cazul de fata devine:

Se vede ca pe durata incarcarii condensatorului sarcina electrica de pe armaturi creste continuu (mai departe se va vedea ca aceasta crestere este exponentiala).

Ecuatia (3.4.18.) devine:

deoarece , conform teoremei condensatorului, .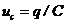

Solutia ecuatiei diferentiale neomogene este :

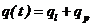unde:

- solutia de regim liber, regim care are loc doar pe durata incarcarii condensatorului;

- solutia de regim fortat sau permanent, valabila dupa trecerea regimului tranzitoriu, reprezentand sarcina maxima la care se incarca condensatorul si cu care se calculeaza capacitatea acestuia.

Solutia de regim liber este solutia ecuatiei diferentiale omogene:

Pentru obtinerea acesteia se rezolva ecuatia caracteristica:

obtinand . Ca urmare, solutia ecuatiei (3.4.21) devine :

unde solutia de regim permanent este:

si reprezinta cantitatea de sarcina pe fiecare armatura (evident, cu semnele plus si minus) cand condensatorul este incarcat.

Determinarea constantei A se face punand conditia initiala privitoare la asigurarea, pe considerente fizice, a continuitatii sarcinii pe armaturile condensatorului in momentul inchiderii intrerupatorului, deci in momentul (ca o consecinta a legii conservarii sarcinii electrice):

Cu alte cuvinte, sarcina 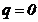dinaintea inchiderii intrerupatorului, respectiv din momentul (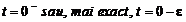) tinde sa ramana nemodificata pentru un interval de timp foarte scurt (), pe durata inchiderii intrerupatorului, pana la momentul (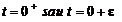). Este vorba de conditii initiale nule.

Acelasi lucru se poate spune despre tensiunea de la bornele condensatorului. Ca urmare , in conditii initiale nule se poate scrie:

sau:

de unde rezulta ca .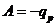

Asadar solutia ecuatiei (3.4.21) devine:

unde, asa cum s-a aratat, solutia de regim permanent este:

Relatia (3.4.3.1) reprezinta teorema capacitatii, valabila dupa incarcarea condensatorului, cand nu mai circula curent prin circuit si .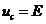

In continuare se poate scrie:

relatie care arata modul de evolutie al sarcinii pe armaturile condensatorului pe durata procesului de incarcare si din care se pot deduce si cazurile pentru , respectiv .

Concluzii

1. Pe toata durata incarcarii condensatorului (durata regimului liber, tranzitoriu) sarcina creste pe armaturile acestuia de la

2. Tensiunea la bornele condensatorului creste si ea conform relatiei:

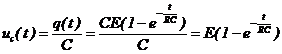La terminarea incarcarii (teoretic la 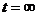), tensiunea devine:

expresie obtinuta din rel. anterioara pentru .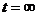

3. Capacitatea condensatorului creste si ea pe durata incarcarii, de la valoare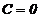a: la 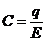pentru 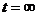(teoretic). Practic, incarcarea completa se atinge dupa un interval de timp unde 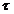reprezinta constanta de timp a circuitului.

Determinarea grafica a acestei constante este evidentiata in figura 4.5.7.

4. Variatia curentului prin circuit se obtine din legea conservarii sarcinii electrice (pentru cazul incarcarii condensatorului):

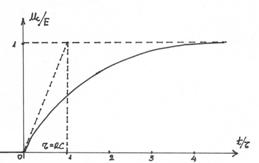
Graficul evolutiei tensiunii la bornele condensatorului si a curentului ( de deplasare) prin condensator, in valori normate, pe durata incarcarii acestuia, sunt prezentate in figura 3.4.9. a si b. Graficul evolutiei sarcinii este asemanator celui al evolutiei tensiunii la bornele condensatorului, la o alta scara.

Constanta de timp a circuitului, 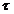, se determina grafic prin ducerea tangentelor la cele doua curbe in origine. Se observa din cele doua grafice ca incarcarea completa se atinge dupa un interval de timp .
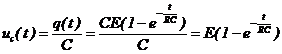