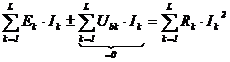Teorema conservarii
puterilor
Numita si teorema bilantului de puteri,
aceasta teorema se enunta altfel:
Suma
algebrica a puterilor primite si cedate de toate laturile unei
retele electrice izolate (autonome) pe la borne este nula (fig.
4.4.4).
Expresia
teoremei este data de relatia:
|
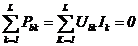
|
|
|
|
|
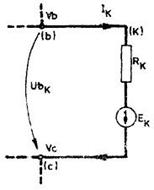
Fig. 4.4.4 Retea
izolata (autonoma)
|
Teorema
conservarii puterilor este o consecinta a primei teoreme a lui Kirchhoff. Astfel, daca expresia
corespunzatoare primei teoreme a lui Kirchhoff
se inmulteste cu potentialul nodului pentru care este
scrisa teorema si se sumeaza expresia obtinuta pentru
toate nodurile retelei, se obtine:
Curentul 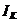 din fiecare
latura intervine in aceasta suma de doua ori: mai intai cu
semnul (+), pentru nodul din care iese (b), apoi cu semnul (-), pentru nodul in
care intra (c).
din fiecare
latura intervine in aceasta suma de doua ori: mai intai cu
semnul (+), pentru nodul din care iese (b), apoi cu semnul (-), pentru nodul in
care intra (c).
Regrupand termenii dupa laturi, se poate scrie:
unde (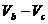 ) este diferenta de potential la bornele laturii k.
) este diferenta de potential la bornele laturii k.
Astfel, teorema este demonstrata.
Forma
de bilant a teoremei
Suma algebrica a puterilor debitate de sursele
din laturile retelei izolate este egala cu suma puterilor consumate
in rezistentele laturilor.
Observatie
Daca
o sursa de t.e.m. are sens opus curentului intr-o latura, aceasta va
intra in expresie cu semnul minus.
Sub forma de bilant teorema se exprima
prin relatia:
|
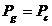
|
(4.4.15. a)
|
respectiv :
|
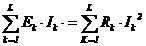
|
(4.4.15.b.)
|
Relatia
(4.4.15.b) se obtine pornind de la ecuatia laturii de circuit, care
se inmulteste cu curentul din latura respectiva si se
sumeaza pentru toate laturile retelei, tinand cont ca:
|
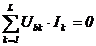 ( conform primei
forme a teoremei conservarii). ( conform primei
forme a teoremei conservarii).
|
|
Se
obtine:
|
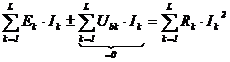
|
(4.4.15.c)
|