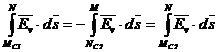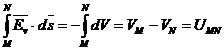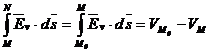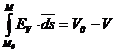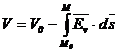Teorema potentialului electrostatic (
si electric)
Enunt: In regim electrostatic circulatia
vectorului camp electric de-a lungul oricarei curbe inchise 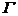 , dusa prin vid, este nula:
, dusa prin vid, este nula:
|
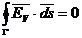
|
(2.2.5.a)
|
Relatia
(2.2.5.a) reprezinta forma integrala a legii. Forma locala este
data de relatia:
|
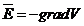
|
(2.2.5.b)
|
Teorema reprezinta un caz
particular al legii inductiei electromagnetice.
Consecintele
teoremei potentialului electrostatic sunt urmatoarele:
a.
In
regim (camp) electrostatic tensiunea electrica dintre doua puncte nu
depinde de drum.
Demonstratie:
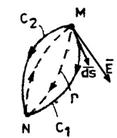
Fie doua puncte, M si N, intr-un camp electrostatic oarecare, in vid, si doua
drumuri oarecare intre aceste puncte (fig. 2.2.2).
|
|
|
Fig. 2.2.2 Consecinta a
|
Se vede ca cele
doua drumuri (C1
si C2) constituie
impreuna drumul inchis 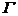 :
:
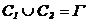
Relatia (2.2.5.a.)
se mai poate scrie sub forma:
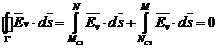
de unde:
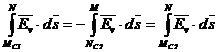
b. Tensiunea
electrica dintre doua puncte aflate in camp electrostatic este
egala cu diferenta potentialelor celor doua puncte.
Deoarece
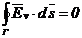 , inseamna ca marimea infinitezimala
, inseamna ca marimea infinitezimala 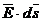 este o diferentiala
totala. Ca urmare se poate introduce o marime scalara V, numita potential electric, astfel incat se poate scrie:
este o diferentiala
totala. Ca urmare se poate introduce o marime scalara V, numita potential electric, astfel incat se poate scrie: 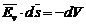 .
.
Semnul minus este introdus prin conventie si are
semnificatia fizica urmatoare: deplasarea unei sarcini unitare
in lungul unei linii de camp, in sens opus acesteia, de pe pamant (in
general de la mare distanta) spre sarcina sau distributia de
sarcini care produce campul, presupune invingerea fortei campului (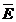 ). Integrand pe
). Integrand pe 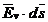 pe un drum oarecare
intre cele doua puncte din camp, se poate scrie:
pe un drum oarecare
intre cele doua puncte din camp, se poate scrie:
sau:
Desi 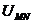 este o marime
scalara, se da acesteia un sens pozitiv, prin conventie,
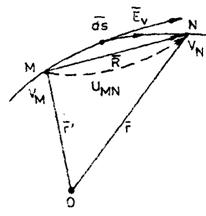
orientat de la primul indice catre cel de-al doilea (fig. 2.2.3).
este o marime
scalara, se da acesteia un sens pozitiv, prin conventie,
orientat de la primul indice catre cel de-al doilea (fig. 2.2.3).
|
|
|
Fig. 2.2.3 Consecinta
b
|
Daca se considera ca punctul 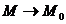 , unde
, unde 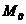 este situat la
distanta mare (
este situat la
distanta mare (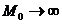 ) de punctul N (de
regula - pe pamant), atunci se
poate aprecia ca punctul N
devine practic acelasi cu M in
raport cu aceasta distanta (
) de punctul N (de
regula - pe pamant), atunci se
poate aprecia ca punctul N
devine practic acelasi cu M in
raport cu aceasta distanta (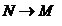 ) si, in aceste conditii, se poate scrie:
) si, in aceste conditii, se poate scrie:
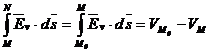
Punand 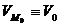 si
si 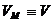 se obtine, in
final:
se obtine, in
final:
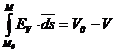
sau:
Relatia (2.2.7) constituie
relatia de definitie a potentialului
electrostatic (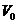 este potentialul
de referinta, in mod obisnuit acesta fiind potentialul
pamantului:
este potentialul
de referinta, in mod obisnuit acesta fiind potentialul
pamantului:  ).
).
Observatie
Relatiile
legate de cele doua consecinte a si b sunt valabile atat in vid, cat si in aer,
dupa cum arata experienta.