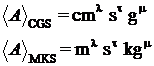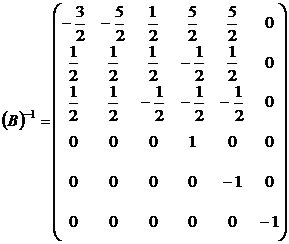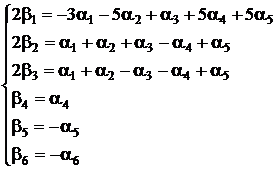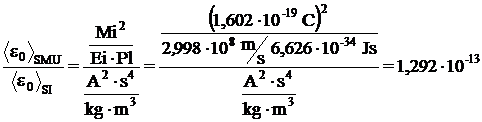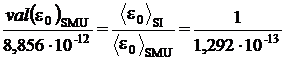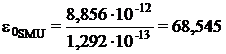DEFINITII SI FORMULE
DEFINITII SI FORMULE
Sistemul International de Unitati de
Masura (SI) este folosit prin
lege atat in tara noastra, cat si pe plan
international. Tabelul urmator cuprinde lista marimilor fizice
fundamentale ale Sistemului International :
Sistemul MKS a fost la origine un sistem de
unitati de masura folosit in tehnica, in domeniul
marimilor fizice mecanice. Dimensiunile sale sunt lungimea, masa si
timpul, iar unitatile de masura corespunzatoare sunt
metrul, kilogramul si secunda.
Sistemul CGS a fost la origine un sistem de
unitati de masura folosit in fizica sau alte
stiinte experimentale si acopera tot domeniul
marimilor fizice mecanice. Dimensiunile sale sunt lungimea, masa si
timpul, iar unitatile de masura corespunzatoare sunt
centimetrul, gramul si secunda.
Formulele dimensionale ale marimilor fizice
sunt aceleasi atat in sistemul CGS, cat si in sistemul MKS, dar
unitatile de masura difera.
Sistemul MKfS a fost la origine un sistem de
unitati de masura folosit in tehnica, in domeniul
marimilor fizice mecanice. Dimensiunile sale sunt lungimea, forta
si timpul, iar unitatile de masura
corespunzatoare sunt metrul, kilogramul-forta si secunda.
Sistemul de unitati de masura anglo-american
are o foarte lunga istorie.
Inca
din timpurile cand a fost elaborata Magna
Carta (1215), a fost necesara includerea in continutul ei a unor
prevederi legate de masurile folosite pentru cereale si vinuri.
Cativa ani mai tarziu, printr-o ordonanta regala, s-a stabilit
o lunga lista de unitati si standarde, care a
ramas in vigoare aproape 600 de ani. De atunci dateaza yardul,
divizat in trei picioare, de cate 12 inch fiecare. Multiplul yardului este
prajina (5,5 yarzi). Interesanta este si originea cuvantului inch. Aceasta unitate de
masura isi trage numele din vechile cuvinte englezesti "unce" (sau "ynche"), care, la randul lor provin din latinul "uncia", care era a douasprezecea
parte din piciorul roman. Vechiul ynche a fost definit de regele David I
al Scotiei, pe la anul 1150. Un ynche
trebuia sa fie egal cu latimea degetului gros al unui
barbat, la baza unghiei. Pentru a se evita incurcaturile sau
confuziile, in practica se masurau latimile degetelor a
trei barbati de staturi de la mic, la mediu si la mare,
dupa care se facea media aritmetica. Pe vremea regelui Edward al
II-lea, la inceputul secolului 14, un inch se definea ca lungimea a trei
seminte de orz uscate, puse cap la cap. Din 1959, oficial, un inch
reprezinta 2,54 centimetri.
Expansiunea
coloniala si comerciala a Angliei a facut ca masurile
de englezesti de lungime, masa, volum sa capete
importanta deosebita la nivelul comertului mondial. Din
acest motiv, chiar dupa dobandirea independentei, Statele Unite ale
Americii nu au adoptat sistemul metric, preferand pastrarea celui
englezesc. Principalul neajuns al sistemului de unitati
anglo-american este legat de transformarile dificile intre
unitatile de masura.
Sistemele CGSe (sistemul absolut
de unitati electrostatice), CGSm (sistemul absolut
de unitati electromagnetice) si CGS Gauss (sistemul absolut de
unitati al lui Gauss) au in comun ca unitati de
masura fundamentale centimetrul, gramul si secunda, dar atribuie
valori conventionale, unitare, adimensionale, unor constante fizice universale
(in CGSe permitivitatea
electrica a vidului este egala cu 1, in CGSm permeabilitatea
magnetica a vidului este egala cu 1, iar in sistemul Gauss aceste
doua constante universale sunt ambele egale cu unitatea. Daca in
domeniul mecanicii folosirea acestor sisteme de unitati de
masura nu are prea mare influenta, in electromagnetism
ecuatiile campului electromagnetic se scriu sub o forma
nerationalizata.
Unitatile de masura tolerate nu
apartin Sistemului International si nici altor sisteme de
unitati de masura, dar se folosesc din motive practice,
istorice sau pur si simplu din inertie. In general, se recomanda
evitarea lor, si cu toate acestea le putem intalni adesea in viata de
zi cu zi.

ASPECTE TEORETICE
Vom
oferi in continuare cateva tabele de transformari, punand in
evidenta doar un numar de marimi fizice mai importante.
|
RELATII INTRE UNITATI DE MASURA MECANICE IN
SISTEMELE SI (MKS) SI CGS
|
|
Marimea fizica
|
Formula dimensionala
|
Unitatea de masura in SI
|
Simbolul unitatii de masura
in SI
|
Unitatea de masura in CGS
|
Simbolul unitatii de masura
in CGS
|
Raportul intre unitatile de masura
|
|
lungime
|
L1M0T0
|
metru
|
m
|
centimetru
|
cm
|
1 m = 102 cm
|
|
timp
|
L0M0T1
|
secunda
|
s
|
secunda
|
s
|
1 s = 1 s
|
|
masa
|
L0M1T0
|
kilogram
|
kg
|
gram
|
g
|
1 kg = 103 g
|
|
viteza
|
L1M0T-1
|
metru pe secunda
|
m/s
|
centimetru pe secunda
|
cm/s
|
1 m/s = 102
cm/s
|
|
acceleratie
|
L1M0T-2
|
metru pe secunda la
patrat
|
m/s2
|
centimetru pe secunda
la patrat
|
cm/s2
|
1 m/s2 = 100
cm/s2
|
|
forta
|
L1M1T-2
|
newton
|
N
|
dyn
|
dyn
|
1 N = 105 dyn
|
|
impuls
|
L1M1T-1
|
kilogram - metru pe secunda
|
kg m/s
|
gram - centimetru pe secunda
|
g cm/s
|
1 kg m/s = 105 g cm/s
|
|
energie
|
L2M1T-2
|
joule
|
J
|
erg
|
erg
|
1 J = 107 erg
|
|
putere
|
L2M1T-3
|
watt
|
W
|
erg pe secunda
|
erg/s
|
1 W = 107 erg/s
|
|
presiune
|
L-1M1T-2
|
pascal
|
Pa
|
barye
|
barye
|
1 Pa = 10 barye
|
|
densitate
|
L-3M1T0
|
kilogram pe metru cub
|
kg/m3 |
gram pe centimetru cub
|
g/cm3
|
1 kg/m3 = 10-3
g/cm3
|
|
momentul fortei
|
L2M1T-2
|
newton - metru
|
N m
|
dyn - centimetru
|
dyn cm
|
1 N m = 107 dyn cm
|
|
moment cinetic
|
L2M1T-1
|
kilogram - metru patrat
pe secunda
|
kg m2/s
|
gram - centimetru patrat
pe secunda
|
g cm2/s
|
1 kg m2/s = 107 g cm2/s
|
|
moment de inertie
|
L2M1T0
|
kilogram - metru patrat
|
kg m2
|
gram - centimetru patrat
|
g cm2
|
1 kg m2 = 107 g cm2
|
Atat
sistemul CGS cat si sistemul MKS sunt sisteme de unitati de
masura coerente. Mai mult, marimile
fizice fundamentale ale celor doua sisteme sunt aceleasi.
Rezulta de aici ca transformarile de unitati de
masura intre cele doua sisteme, revin, de fapt, la redefinirea
unitatilor de masura fundamentale :

adica noile unitati de masura sunt
multipli ai vechilor unitati, factorii Ki fiind doar coeficienti numerici. Conditia
de omogenitate dimensionala corespunzatoare unei legi a fizicii de
forma :

este :

si devine :

In virtutea conditiei de omogenitate,  , rezultand
, rezultand
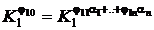
s.a.m.d., astfel incat toti coeficientii
numerici se simplifica, ramanandu-ne :
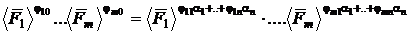
Concluzia este aceea ca date fiind doua sisteme de unitati de masura
coerente, bazate pe aceleasi marimi fizice fundamentale, formulele
dimensionale ale marimilor fizice au aceeasi forma in ambele
sisteme, diferite fiind doar unitatile de masura.
Pornind de la aceasta concluzie, putem gasi o relatie
generala dupa care se poate face transformarea unei unitati
de masura din MKS in CGS sau invers.
Avem :
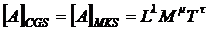
Atunci :
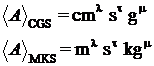
Rezulta :

Deci :

astfel incat, in final obtinem :

In
tehnica, s-a folosit in paralel cu sistemul MKS sistemul MKfS (metru - kilogram-forta
- secunda). Marimile fizice fundamentale ale celor doua sisteme
sunt diferite. Asa cum am vazut sistemul MKS este bazat pe lungime (L), timp (T) si masa (M),
in timp ce sistemul MKfS are ca marimi fundamentale lungimea (L), timpul (T) si forta (F).
In aceste conditii, formulele
dimensionale ale marimilor fizice sunt diferite in cele doua sisteme.
Sa
luam ca exemplu puterea mecanica, definita ca lucrul mecanic
efectuat in unitatea de timp :
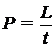
obtinem urmatoarele relatii
dimensionale

unitatile de masura
corespunzatoare sunt

Daca tinem cont ca 1 kgf = 9,8 N,
rezulta

adica unitatea de masura a puterii in MKfS
este de 9,8 ori mai mare decat in SI.
In
general, relatiile de transformare ale formulelor dimensionale si ale
unitatilor de masura din sistemul MKfS in Sistemul
International se scriu astfel:

Pentru
marimile mecanice mai importante, tabelul de transformari intre MKS
si CGS este urmatorul :
|
RELATII INTRE UNITATI DE MASURA MECANICE IN
SISTEMELE SI (MKS) SI MKfS
|
|
Marimea fizica
|
Unitatea de masura in SI
|
Simbolul unitatii de masura
in SI
|
Unitatea de masura in MKfS
|
Simbolul unitatii de masura
in MKfS
|
Raportul intre unitatile de
masura
|
|
lungime
|
metru
|
m
|
metru
|
cm
|
1 m = 1 m
|
|
timp
|
secunda
|
s
|
secunda
|
s
|
1 s = 1 s
|
|
masa
|
kilogram
|
kg
|
kilogram
|
kg
|
1 kg = 1 kg = 1/9,8 kgf s2/m
|
|
viteza
|
metru pe secunda
|
m/s
|
metru pe secunda
|
m/s
|
1 m/s = 1m/s
|
|
acceleratie
|
metru pe secunda la
patrat
|
m/s2
|
metru pe secunda la
patrat
|
m/s2
|
1 m/s2 = 1 m/s2
|
|
forta
|
newton
|
N
|
kilogram-forta
|
kgf
|
1 N = 1/9,8 kgf
|
|
energie
|
joule
|
J
|
kilogram-forta -
metru
|
kgf m
|
1 J = 1/9,8 kgf m
|
|
putere
|
watt
|
W
|
kilogram-forta -
metru pe secunda
|
kgf m/s
|
1 W = 1/9,8 kgf m/s
|
|
presiune
|
pascal
|
Pa
|
kilogram-forta
pe metru patrat
|
kgf/m2
|
1 Pa = 1/9,8 kgf/m2
|
Ne
vom margini in continuare sa prezentam, fara prea
multe amanunte, unitatile de masura ale unor
marimi electromagnetice in SI, CGSm0 si CGSe0
:
|
UNITATI DE
MASURA
|
|
Marimea fizica
|
SI
|
CGSm
|
CGSe
|
|
Intensitatea curentului electric (I)
|
amper (A)
|
biot (Bi)
|
statamper (stA)
|
|
Sarcina electrica (Q)
|
coulomb (C)
|
abcoulomb (abC)
|
statcoulomb (stC)
|
|
Tensiunea electrica (U)
|
volt (V) |
abvolt (abV)
|
statvolt (stV)
|
|
Rezistenta electrica (R)
|
ohm (W)
|
abohm (abW)
|
statohm (stW)
|
|
Capacitatea electrica (C)
|
farad (F)
|
abfarad (abF)
|
statfarad (stF)
|
|
Inductanta (L)
|
henry (H)
|
abhenry (abH)
|
stathenry (stH)
|
|
Intensitatea campului electric (E)
|
volt pe metru (V/m)
|
abvolt pe centimetru (abV/cm)
|
statvolt pe centimetru (stV/cm)
|
|
Inductia campului magnetic (B)
|
tesla (T)
|
gauss (Gs)
|
stattesla (stT)
|
Alaturi
de unitatile de masura apartinand diferitelor sisteme
de unitati de masura, putem intalni si unitatile
de masura tolerate. Acestea sunt mentinute fie
datorita caracterului lor istoric, fie pentru ca utilizarea lor este
raspandita in practica. Vom mentiona in continuare cateva
dintre cele mai cunoscute unitati de masura tolerate:
|
Nume
|
Simbol
|
Marimea
masurata
|
Relatia cu
unitatea SI
|
|
tona
|
t
|
masa
|
1 t = 1000 kg
|
|
carat
|
ct
|
masa
|
1 ct = 2 10-4
kg
|
|
unitate
atomica de masa
|
uam
|
masa
|
1 uam = 1,67 10-27
kg
|
|
kilogram-forta
|
kgf
|
forta
|
1 kgf = 9,8 N
|
|
bar
|
bar
|
presiunea
|
1 bar = 100000 Pa
|
|
atmosfera
fizica
|
atm
|
presiunea
|
1 atm = 101325 Pa
|
|
atmosfera
tehnica
|
at
|
presiunea
|
1 at = 98000 Pa
|
|
milimetru
coloana de mercur (torr)
|
mmHg
(torr)
|
presiunea
|
1 mmHg = 133,32 Pa
|
|
milimetru
coloana de apa
|
mmH2O
|
presiunea
|
mmH2O =
9,8 Pa
|
|
calorie
|
cal
|
caldura
|
1 cal = 4,18 J
|
|
kilowatt-ora
|
kWh
|
energia
|
1 kWh = 3,6 106
J
|
|
electron-volt
|
eV
|
energia
|
1 eV = 1,6 10-19
J
|
|
cal-putere
|
CP
|
puterea
|
1 CP = 735,5 W
|
|
litru
|
l
|
volumul
|
1 l = 0,001 m3
|
|
angstrom
|
|
lungimea
|
1 Å = 10-10 m
|
Cu
titlu de curiozitate, deoarece nu mai au de mult timp semnificatia originala,
vom mentiona si cateva unitati de masura
romanesti :
|
Nume
|
Marimea
masurata
|
Relatia cu
unitatea SI
|
|
litra
|
volum
|
0,322 dm3
in Muntenia, 0,380 dm3 in Moldova
|
|
litra
|
masa
|
0,318 kg in
Muntenia, 0,323 kg in Moldova
|
|
oca
|
volum
|
1,288 dm3
in Muntenia, 1,250 dm3 in Moldova
|
|
oca
|
masa
|
1,71 kg in
Muntenia, 1,291 kg in Moldova
|
|
banita
|
volum de cereale
|
circa 34 dm3
|
|
ar
|
suprafata
de teren
|
100 m2
|
|
cot
|
lungime
|
0,664 m in
Muntenia, 0,637 m in Moldova
|
|
vadra
|
volum
|
12,88 dm3
in Muntenia, 12,50 dm3 in Moldova
|
|
prajina
|
lungime
|
5,9 m in Muntenia,
6,69 m in Moldova
|
|
prajina
|
suprafata
de teren
|
202,8 m2
in Muntenia, 179 m2 in Moldova
|
|
dram
|
volum
|
3,22 cm3
in Muntenia, 3,80 dm3 in Moldova
|
|
dram
|
masa
|
3,18 g in Muntenia,
3,23 g in Moldova
|
Iata
si cateva unitati de masura anglo-americane :
1 inch = 2,54 cm
1 picior = 0,3048 m
1 yard = 0,9144 m
1 mila terestra = 1,6093 km
1 mila marina = 1,852 km
1 acru = 0,4047 ha
1 gallon (SUA) = 3,7854 l, 1 gallon (MB) = 4,546
l
1 pinta (SUA) = 0,4732 l, 1 pinta (MB)
= 0,5682 l
1 uncie = 28,3495 g
1 livra (funt) = 453,59 g
In
stransa legatura cu sistemele de unitati de
masura se gasesc si valorile constantelor fizice
universale. Iata, in continuare, un tabel cu cele mai reprezentative
dintre acestea :
|
Constante fizice universale
|
|
Denumirea constantei
|
Simbol
|
Valoarea in SI
|
|
Accceleratia gravitationala
la latitudinea de 45 , la nivelul marii
|
g
|
g = 9,80616 m/s2
|
|
Constanta gravitationala
|
k
|
k 10-11 N m2/kg2
|
|
Constanta gazelor ideale
|
R
|
R = 8310 J/(kmol K)
|
|
Volumul molar in conditii normale
|
Vm |
Vm = 22,4146 m3/kmol
|
|
Numarul lui Avogadro
|
NA
|
NA 1026 kmol-1
|
|
Constanta lui Boltzmann
|
k
|
k 10-23 J/K
|
|
Numarul lui Faraday
|
F
|
F = 96501,2 C/echiv-gram
|
|
Masa de repaus a protonului
|
mp
|
mp 10-27 kg
|
|
Masa de repaus a electronului
|
me
|
me 10-31 kg
|
|
Sarcina electrica a electronului
|
e
|
e 10-19 C
|
|
Sarcina specifica a electronului
|
e/
me
|
e/
me 1011
C/kg
|
|
Viteza luminii in vid
|
c
|
c 108 m/s
|
|
Constanta lui Planck
|
h
|
h 10-34 J s
|
|
Constanta lui Rydberg
|
R
|
R 107 m-1
|
|
Permitivitatea electrica absoluta
a vidului
|
e
|
e 10-12 F/m
|
|
Permeabilitatea magnetica absoluta
a vidului
|
m
|
m p 10-7
H/m
|
|
Lungimea de unda Compton
|
L
|
L 10-12
m
|
|
Constanta Stefan-Boltzmann
|
s
|
s 10-8
W/(m2 K4)
|
EXEMPLU
Sistem
de unitati de masura bazat pe constante fizice universale
Intr-un sistem
de unitati de masura, asa cum este si Sistemul
International, unitatile de masura fundamentale sunt
stabilite in mod arbitrar. Pentru a evita definirea arbitrara a
unitatilor de masura fundamentale, s-ar putea imagina un
sistem de unitati de masura bazat pe un numar de
constante fizice universale. Definirea arbitrara
a unitatilor de masura ar fi inlocuita in acest caz cu
atribuirea unor valori egale cu unitatea acestor constante fizice.
Sa luam in discutie
urmatoarea propunere de sistem de unitati de masura :
|
constanta
universala
|
valoarea si
unitatea de
masura in SI
|
formula
dimensionala
in
SI
|
noua
formula
dimensionala
|
noua valoare
si unitate
de masura
|
|
viteza luminii
in vid
|
c = 2,998 108 m/s
|
LT-1
|
C
|
c = 1 Ei (einstein)
|
|
constanta lui Planck
|
h = 6,626 10-34 Js
|
L2MT-1
|
H
|
h = 1 Pl
(planck)
|
|
constanta
gravitationala
|
g =
6,673 10-11 Nm2/kg2
|
L3M-1T-2
|
G
|
g =
1 Ne
(newton)
|
|
sarcina
electronului
|
e = 1,602 10-19 C
|
TI
|
E
|
e = 1 Mi
(millikan)
|
|
constanta lui
Boltzmann
|
k = 1,381 10-23 J/K
|
L2MT-2Q-1
|
K
|
k = 1 Bo
(boltzmann)
|
|
numarul lui
Avogadro
|
NA = 6,023 1026
kmol-1
|
N-1
|
N
|
NA = 1 Av
(avogadro)
|
Ne propunem
sa determinam formula dimensionala si valoarea unei
marimi fizice in noul sistem al marimilor fizice fundamentale (SMU).
fie formulele dimensionale ale unei marimi A in cele doua sisteme de
unitati de masura :

problema pe care trebuie s-o rezolvam
consta in a gasi expresiile exponentilor b1, b2,
b6
in functie de exponentii a1, a2, a6
si formulele dimensionale ale noilor marimi fundamentale
mai intai, vom inlocui in a doua formula
dimensionala noile dimensiuni cu cele vechi :

am efectuat astfel transformarea formulei
dimensionale a marimii A,
obtinand :

deoarece exponentii celor doua
modalitati de exprimare a formulei dimensionale a marimii A in SI trebuie sa fie egali,
rezulta :

putem transcrie acest sistem de ecuatii sub
forma matriciala :

sau, pe scurt :

unde (B) este
matricea dimensionala de trecere de la SMU la SI.
determinantul matricei de transformare este
unitar, iar inversa matricei de transformare este :
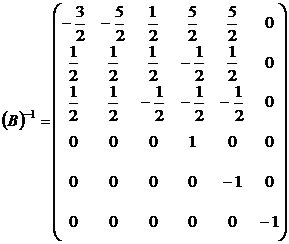
in aceste conditii matricea (b)
este data de :

sau :
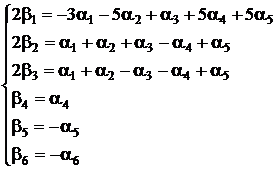
formula dimensionala si unitatea de
masura ale marimii A
in SMU devin :

Fie o alta constanta
fizica universala: e0 =8,856 10-12 F/m. Deoarece :

Rezulta :

si :

In aceste conditii :

sau :

Conform acestei formule, noua unitate de masura a
permitivitatii este :

Raportul unitatilor de masura din cele
doua sisteme de unitati este :
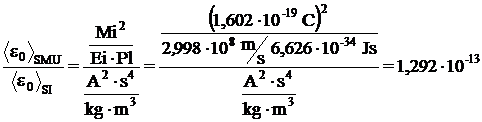
Conform
teoremei fundamentale a unitatilor de masura, raportul
valorilor numerice ale permitivitatii electrice absolute a vidului in
cele doua sisteme de unitati de masura este invers
proportional cu raportul unitatilor de masura.
Rezulta :
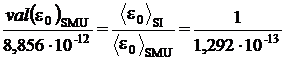
sau :
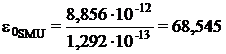
sau :

Am
urmarit prin acest exemplu sa rezolvam cea mai complexa
problema de transformare a unitatii de masura a unei
marimi fizice (si implicit a valorii sale numerice) dintr-un sistem
de unitati de masura bazat pe anumite marimi fizice
fundamentale in alt sistem de unitati de masura, bazat pe
alt set de marimi fundamentale. Concluzia este urmatoarea :
Operatia de transformare a valorii si
unitatii de masura este posibila daca se cunosc
relatiile dimensionale si numerice intre marimile fizice
fundamentale ale celor doua sisteme de unitati de
masura, precum si formula dimensionala si valoarea
numerica a marimii considerate intr-unul din cele doua sisteme
de unitati de masura.

TEMA
Exprimati
in milibari presiunea de 752 torr.
O forta de 14 kgf face un
lucru mecanic de 1250000 erg. Calculati deplasarea punctului de
aplicatie al fortei.
Diferenta
de presiune intre gazul dintr-o incinta si aerul atmosferic este de
20 mm coloana de mercur. Exprimati diferenta de presiune in centimetri
coloana de apa.
Un
motor de 50 CP functioneaza jumatate de ora. Exprimati
lucrul mecanic facut in kilowati-ora.
Puterea
calorifica a unui carbune este 6000 kcal/kg. Exprimati puterea
calorifica a carbunelui in Sistemul International.
Un
grad Celsius corespunde ca diferenta de temperatura cu 1,8 grade
Fahrenheit, iar temperatura de 0 C reprezinta o valoare de 32 F. Temperatura
normala a corpului omenesc este de 36 C. Ce
valoarea are temperatura normala a corpului intr-o tara care
foloseste termometre gradate in scara Fahrenheit ?
Inaltimea unui american este
de 5 picioare. Este acesta inalt sau scund ?
"A
fost prins cu ocaua mica" este o expresie care dateaza din perioada
Unirii Principatelor. Cel care vinde cu ocaua mica era persoana care
vindea in Muntenia avand ca unitate de masura ocaua
moldoveneasca. Daca ati fi cheltuit 100 de lei cumparand
carne de porc, ce suma ar fi castigat nemeritat acela care vindea cu
ocaua mica ?
Cati
electron-volti are un kilowatt-ora ?