Ciclicitatea proceselor economice si crizele economice
Incertitudinea este o
caracteristica esentiala a economiei de piata,
intemeiata pe proprietatea privata si deciziile individuale ale
agentilor economici. Extinderea ariei de cuprindere a economiei de
piata in decursul ultimelor secole si mai ales accelerarea
ritmului cresterii economice in conditiile progresului stiintific
si tehnic din secolul XX au dus la accentuarea oscilatiilor si
fluctuatiilor care insotesc aceasta economie [65]. Apar astfel
diferite forme de fluctuatii economice, incepand cu fluctuatiile
conjuncturale, de mica amplitudine, continuand cu fluctuatiile
periodice mai pronuntate care se manifesta in mod repetat sub
forma de crize economice, imprimand activitatii economice un
caracter ciclic.
Ciclicitatea
reprezinta acea forma de miscare a activitatii
economice dintr-o tara, in care
fazele de expansiune alterneaza cu cele de stagnare si descrestere.
Ciclul economic reprezinta unitatea de timp pentru miscarea
ciclica.
Ca
forma de miscare a reproductiei si cresterii
economice, ciclicitatea se caracterizeaza sub doua aspecte
principale:
Succesiunea si
repetabilitatea in timp a unor stari ale economiei, numite fazele
ciclului, care seamana in linii generale de la un ciclu la altul, in
fiecare faza, starea economiei si performantele sale agregate -
ritmul cresterii produsului intern brut, o productie industriala
si agricola, gradul de ocupare a fortei de munca,
evolutia eficientei economice, dinamica nivelului de trai si a
calitatii vietii - au anumite caracteristici si
inregistreaza fluctuatii semnificative de la o faza la alta;
In inlantuirea
lor, aceste faze pregatesc premisele ce conduc la schimbari
calitative in conditiile cresterii economice si ale
reproductiei, care le asigura continuitatea ca si progresul
economic.
Ciclul economic surprinde succesiunea in timp a
conditiilor si rezultatelor reproductiei si cresterii
economice. Un ciclu economic sau un ciclu al afacerilor se caracterizeaza
prin cresterea simultana a nivelului majoritatii
activitatilor economice, urmata de o scadere a acestor
niveluri, dupa care urmeaza faze de expansiune a ciclului
urmator.
Pentru evidentierea fluctuatilor ciclice se
prelucreaza serii cronologice de date referitoare la anumiti
indicatori: produsul intern brut si net, volumul vanzarilor cu
amanuntul sau cu ridicata, nivelul dobanzilor bancare, nivelul
somajului, venitul personal etc. Prelucrarea statistica a seriilor
respective permite identificarea trendului sau tendintei principale, a
variatiei sezoniere si a variatiei intamplatoare, pentru
evidentierea componentei ciclice, a variatiei totale. Cu ajutorul
unor metode statistice adecvate (vezi serii cronologice!) se calculeaza
curba trendului, care reprezinta variatia medie a fenomenului
analizat.
Un alt mod, mai complex, de a pune in evidenta
ciclurile economice este acela de determinare a ciclurilor limita
corespunzatoare unui sistem dinamic ce modeleaza fenomenul economic
studiat.
Incepand cu anii '30, observam o proliferare a
modelelor formale care folosesc variante de tipul investitie-accelerator
si consum-multiplicator (Harrod 1936, Kalecki 1937, Samuelson 1939,
Metzler 1941, Hicks 1950). O clasa mai generala
de modele sunt cele care au la baza principiul capitalului ajustat (sau
"acceleratorul flexibil"): investitiile curente sunt egale cu raportul
dintre capitalul dorit (asteptat) si cel actual. Stocul asteptat
variaza direct cu outputul. Investitiile nete depind de asemenea,
direct de output si invers de stocul initial de capital (Kalecki
1935, Kaldor 1940, Goodwin 1951). Dinamica acestor modele este determinata
de neliniaritati. Neliniaritatile sunt folosite in teoria
ciclurilor economice si au fost sistematic explorate in literatura
recenta de specialitate. Astfel, metodele analitice ale teoriei
bifurcatiei si teoriei catastrofelor au fost aplicate in analizarea
fluctuatiilor economice, a crizelor economice, depresiunilor, revenirilor
rapide.
Studiul ciclurilor economice este
foarte vast, foloseste termeni din macroeconomie si are o mare
aplicabilitate in cresterea economica, economia monetara,
studiul inflatiei, instabilitatea financiara si ajustarea
graduala a preturilor. Iata cateva din rezultate matematice
privind ciclurile economice:
A. Teorema Poincaré-Bendixson si aplicatiile sale in economie
Fie sistemul bidimensional de ecuatii
diferentiale ordinare

unde  si functiile
f si g sunt netede in raport cu x. Un studiu asupra ciclurilor limita
corespunzatoare unui astfel de sistem este dat de Ye (1986).
si functiile
f si g sunt netede in raport cu x. Un studiu asupra ciclurilor limita
corespunzatoare unui astfel de sistem este dat de Ye (1986).
Punctul x* este punct limita pentru x daca
exista un sir astfel incat  unde Wt(x)
este curentul (fluxul) sistemului.
unde Wt(x)
este curentul (fluxul) sistemului.
Teorema Poincaré-Bendixson. O multime limita a unui flux plan,
compacta, nevida si care nu contine puncte fixe este o
orbita inchisa. Daca traiectoria prin x intra si nu
paraseste un domeniu inchis, marginit D, care nu
contine puncte stationare atunci exista cel putin o
orbita periodica in D.
Sa notam ca aceasta teorema nu
exclude posibilitatea unor cicluri limita multiple.
Teorema Bendixson.
Sa presupunem ca f si g au derivate partiale de ordinul
intai continue pe D. Daca suma  are semn constant pe
tot domeniul D atunci nu exista solutie periodica pe D.
are semn constant pe
tot domeniul D atunci nu exista solutie periodica pe D.
Aceasta teorema reda conditiile in
care putem exclude existenta unor cicluri pe un domeniu.
Teorema De Baggis. Fie un sistem structural
stabil. Atunci el are numai un numar finit de cicluri limita in
domeniul D care sunt alternativ stabile si instabile in sens asimptotic.
Aceste teoreme au multiple si
importante aplicatii in economie (Schinasi 1982, Semmler 1985, 1986). O
mare importanta o are, de fapt,
Ciclul comercial al lui Kaldor (1940).
Modelul
este studiat de Kaldor in 1940. El este prezent in diferite forme in teoria
afacerilor. Prezentarea originala a fost nematematica si a fost
studiata cu tehnici bazate pe grafica (Marama 1946). Primul studiu
riguros matematic a fost dat de Ichimura in 1955, apoi a fost studiat de Chang
si Smyth in 1971, cu ajutorul teoremei Poincaré-Bendixson. Modelul propus
de acestia este

unde Y, K, S si I
reprezinta venitul real, capitalul, functia consum si
functia investitie neta, respectiv. Se mai presupune ca SK
< 0 si 
Se poate observa ca
produsul valorilor proprii este (SKIY - SYIK)
in punctul de echilibru. Acest numar trebuie sa fie pozitiv pentru a
exclude posibilitatea aparitiei unui punct sa. Suma valorilor proprii
este (IY - SY) + IK care trebuie de asemenea
sa fie strict pozitiva daca dorim ca echilibrul determinat
sa fie instabil. Chang si Smyth au demonstrat urmatoarea
teorema:
Teorema (Chang si
Smyth) Daca sistemul considerat este definit pe 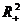 si are
urmatoarele proprietati:
si are
urmatoarele proprietati:
a) IK < SK
< 0; IY > 0; SY > 0;
b) la echilibrul (K0,Y0),
α(IY - SY) + IK > 0 si SKIY
< SYIK;
c)  intersecteaza axa 0K intr-un numar
finit K(0) > 0;
intersecteaza axa 0K intr-un numar
finit K(0) > 0;
d) 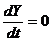 intersecteaza
axa 0Y pentru Y1 > Y0 finit iar
intersecteaza
axa 0Y pentru Y1 > Y0 finit iar 
e)
sistemul este structural stabil
atunci fiecare
traiectorie este un ciclu limita sau aproximeaza un ciclu limita
(fig.3.29):
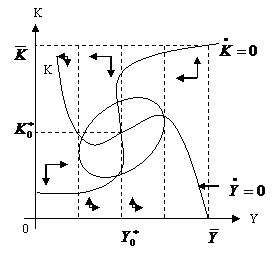
-
Fig.3.29 -
Aceasta
teorema gaseste conditiile de existenta ale
ciclului limita dar nu spune nimic despre unicitatea sa sau despre tipul
oscilatiilor.
Lorenz a incercat sa rezolve problema
unicitatii ciclului limita folosind:
Teorema (Levinson and Smyth 1942). Ecuatia generalizata de tip
Liénard
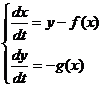 sau
sau 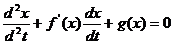 are o solutie
unica daca sunt satisfacute conditiile:
are o solutie
unica daca sunt satisfacute conditiile:
a) f' si g sunt de
clasa C'
b) pentru orice x1
> 0 si x2 > 0 astfel incat -x1 < x < x2
are loc f'(x1)<0
si f'(x2)>0
c) xg(x) > 0 oricare ar
fi x ≠ 0
d) 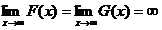 unde
unde  ;
; 
e) G(-x1) = G(x2)
Aplicand
aceasta teorema sistemul initial poate fi scris sub forma
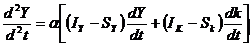
si diferentiind in raport cu timpul
obtinem
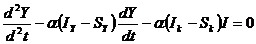
Aplicand
teorema si presupunand ca stocul de capital este determinat de
deciziile economice, adica  unde S = S(Y) si
ca expresia W(Y) = IK
- SK este independenta de stocul de capital ecuatia
poate fi rescrisa astfel
unde S = S(Y) si
ca expresia W(Y) = IK
- SK este independenta de stocul de capital ecuatia
poate fi rescrisa astfel
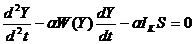
Cu aceste presupuneri,
destul de acceptabile Lorenz (1986) a demonstrat ca daca
investitia si economiile sunt functii simetrice in raport cu Y
atunci sistemul initial considerat admite un ciclu limita unic.
Prin importanta neliniaritatii, ciclul
comercial al lui Kaldor stimuleaza inca cercetarea. Recent Grasman
si Wenzel (1994) au aratat ca in acest model este posibila
coexistenta unui echilibru stabil cu un ciclu limita stabil.



 are semn constant pe
tot domeniul D atunci nu exista solutie periodica pe D.
are semn constant pe
tot domeniul D atunci nu exista solutie periodica pe D.
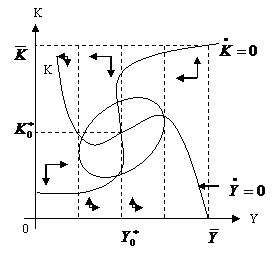
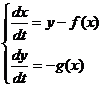 sau
sau  ;
; 