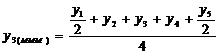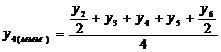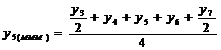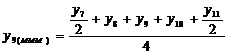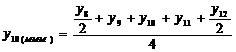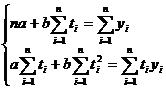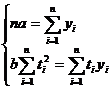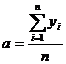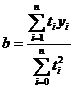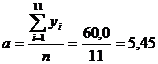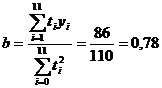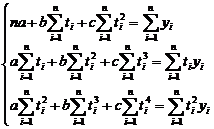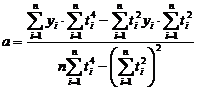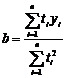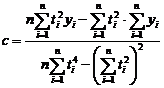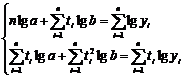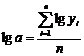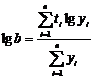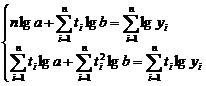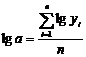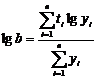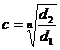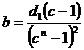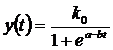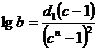Evaluarea econometrica a
trendului
Trendul reprezinta acea componenta
sistematica, ce reflecta tendinta generala a unui fenomen,
ca rezultat al influentei unor factori esentiali.
Factorii care
determina trendul sunt formati in raport cu insusirea
esentiala a fenomenului studiat si au o actiune
continua care provoaca variatii sistemice lente.
Succesiunea
regulata a variatiilor trendului se caracterizeaza printr-o
consecventa in ceea ce priveste modificarea sensului,
aceasta durata fiind relative mare, mentionandu-se o
perioada cuprinsa intre 10 si 15 ani.
In aceste
conditii, relevanta evolutiei unui fenomen este data de o
serie formata din peste 10 termeni.
Exemplul
1. Vom connsidera ca prim exemplu Evolutia
numarului sosirilor turistilor din Romania, in perioada 1991-2006. Grafic, evolutia sosirilor este ilustrat in figura 3
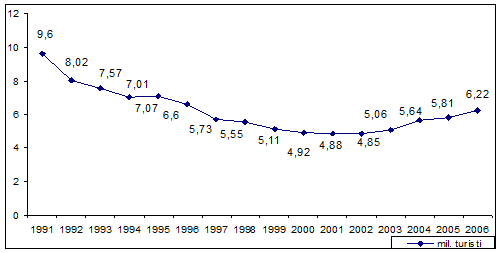
Figura 3 Evolutia numarului sosirilor turistilor
din Romania,
in perioada 1991-2006.
Tinand seama de numarul
termenilor seriei si modul in care au fost inregistrati seria de date
poate fi consideranta relevant. In ceea ce priveste tendinta
generala, dupa cum se poate observa, acesta are o evolutie
neliniara (posibil parabolica), liniaritatea fiind o evolutie
particulara care poate fi intalnita numai in anumite situatii.
Trendul este
evidentiat prin acea traiectorie evolutiva cu caracter de "medie",ca
urmare a procesului de ajustare, adica o netezire a seriei de timp,
facand abstractie de erorile datorateinfluentei factorilor
intamplatori.
Determinarea si
analiza trendului se bazeaza pe metodele specifice care cuprind metode
mecanice si metode analitice, aplicate in general, ca urmare a
reprezentarii grafice care sugereaza cel mai bine tendinta de
evolutie a fenomenului analizat.
1. Ajustarea
mecanica
Metodele mecanice
sunt cele mai simple metode care descriu tendinta evolutiva a
fenomenului cu ajutorul indicatorilor seriei de timp, in cadrul lor
inscriindu-se metoda sporului mediu, metoda
indicelui mediu, metoda mediilor mobile.
r
Metoda mediilor mobile (MMM)
Metoda mediilor
mobile este o metoda de ajustare care vizeaza eliminarea prin "nivelare"
a valorilor care se abat de la tendinta acesteia. Metoda este
utilizata cu precadere in studierea evolutiei fenomenelor cu
oscilatii de tip sezonier sau ciclic.
Valorile trendului sunt reprezentate de mediile mobile partiale
determinate din termenii seriei cronologice. Se numesc medii mobile deoarece
sunt obtinute pe baza termenilor preluati prin glisare, (sau
alunecare in sensul ca, se scoate din relatie primul termen din media
anterioara si se preia urmatorul din seria initiala).
Metodologia de determinare a tendintei este bazata pe medii
mobile partiale si impune utilizarea unui numar de termeni (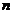 ) care incheie o fluctuatie completa: pentru date
lunare se folosesc medii mobile de 12 termeni, in cazul informatiilor
trimestriale sunt aplicate mediile mobile din 4 termeni etc.
) care incheie o fluctuatie completa: pentru date
lunare se folosesc medii mobile de 12 termeni, in cazul informatiilor
trimestriale sunt aplicate mediile mobile din 4 termeni etc.
Stabilirea tendintei unui fenomen prin aplicarea metodei de ajustare
cu metoda mediilor mobile este destul de putin utilizata, deoarece:
trendul
determinat are un numar de termeni mai mic decat cel al seriei
initiale cercetate(seriile impare pierd la fiecare capat 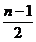 valori, iar cele pare
valori, iar cele pare 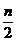 termeni);
termeni);
valorile
trendului nu se apropie foarte mult de cele reale, tinzand de cele mai multe
ori spre cele maxime sau minime, ceea ce nu confera o calitate
ridicata metodei;
nu
ofera posibilitatea previzionarii tendintei pentru
urmatoarele perioade.
r
Ajustarea seriilor de timp cu numar
impar de termeni utilizand MMM
Aplicarea MMM presupune calcularea
termenilor trendului cu ajutorul mediei aritmetice formata dintr-un
numar impar de termeni preluati din serie prin glisare. Numarul
termenilor este stabilit in concordanta cu ciclicitatea, astfel:
pentru o serie cronologica
formata din 9 termeni, valorile empirice (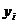 cu
cu 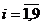 ) si cele ajustate (
) si cele ajustate (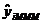 cu
cu 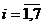 ), se prezinta astfel:
), se prezinta astfel:
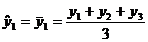
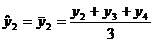
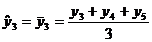
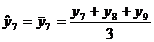
pentru o serie cronologica
formata din 25 termeni (ciclicitate completa la 5 ani), valorile
empirice (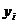 cu
cu 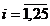 ) si cele ajustate (
) si cele ajustate ( cu
cu 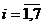 ), se prezinta astfel:
), se prezinta astfel:
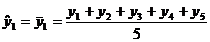
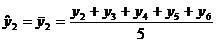
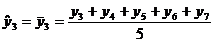
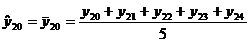
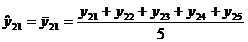
generalizand, pentru o serie
cronologica formata din t termeni (ciclicitate completa
la n perioade), valorile empirice (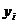 cu
cu 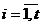 ) si cele ajustate (
) si cele ajustate ( cu
cu 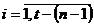 ), se prezinta astfel:
), se prezinta astfel:
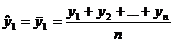
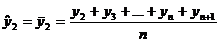
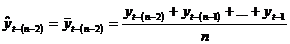
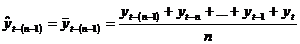
Observatie Numarul termenilor
trendului (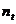 ) este cu
) este cu 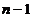 mai mic decat cel al
seriei initiale (
mai mic decat cel al
seriei initiale (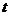 ):
):
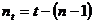
unde: 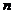 - reprezinta numarul perioadelor dupa care se
inchide o ciclicitate completa.
- reprezinta numarul perioadelor dupa care se
inchide o ciclicitate completa.
Exemplul La SCR cu 9
termeni (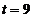 ) si ciclicitate completa de trei ani (
) si ciclicitate completa de trei ani (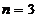 ), numarul termenilor trendului, conform (4), va fi:
), numarul termenilor trendului, conform (4), va fi: 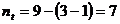 termeni.
termeni.
Exemplul 3. La SCR cu 25 termeni (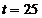 ) si ciclicitate completa de cinci ani (
) si ciclicitate completa de cinci ani (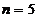 ), numarul termenilor trendului conform (4), este:
), numarul termenilor trendului conform (4), este: 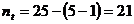 termeni.
termeni.
r
Ajustarea seriilor de timp cu numar
par de termeni utilizand MMM
In cazul seriilor de timp cu numar par de termeni, MMM implica:
A.
fie
utilizarea mediilor mobile provizorii si definitive, parcurgand astfel
doua trepte pana la formarea valorilor trendului;
B.
fie
aplicarea unei singure trepte metodologice prin care se foloseste media
mobila cronologica simpla.
Ajustarea unei astefel de serii cu metoda mediilor mobile este
aplicata, in general, pentru serii cronologice cu oscilatii periodice
la nivelul trimestrelor.
Tabelul 1. Varianta
A de aplicare a MMM
pentru
serii cu numar par de termeni
|
Anul
|
Trim.
|
Valori empirice
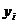
|
Medii mobile provizorii
|
Medii mobile definitive
(valori ajustate=valorile
trendului

|
|
I
|
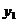
|
|
|
|
|
|
|
II
|
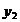
|
|
|
|
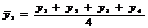
|
|
|
III
|
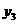
|
|
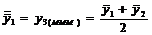
|
|
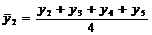
|
|
|
IV
|
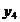
|
|
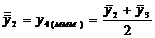
|
|
|
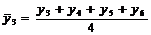
|
|
|
I
|
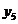
|
|
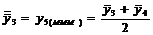
|
|
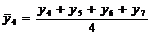
|
|
|
II
|
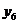
|
|
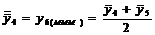
|
|
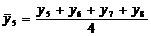
|
|
|
III
|
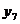
|
|
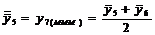
|
|
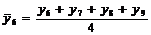
|
|
|
IV
|
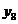
|
|
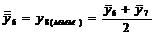
|
|
|
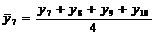
|
|
|
I
|
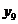
|
|
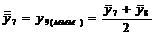
|
|
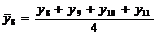
|
|
|
II
|
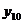
|
|
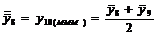
|
|
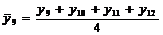
|
|
|
III
|
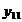
|
|
|
|
|
|
|
IV
|
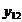
|
|
|
Daca dispunem de informatii statistice privind variabila  preluate pe trimestrele ultimilor trei ani, se
poate aplica MMM in cele doua variante (A si B), conform tabelelor 1
si respectiv 2
preluate pe trimestrele ultimilor trei ani, se
poate aplica MMM in cele doua variante (A si B), conform tabelelor 1
si respectiv 2
Tabelul Varianta A de aplicare a MMM
pentru
serii cu numar par de termeni
|
Anul
|
Trim.
|
Valori empirice
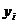
|
Medii mobile definitive
(valori ajustate=valorile
trendului

|
|
I
|
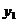
|
|
|
II
|
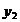
|
|
|
III
|
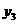
|
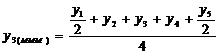
|
|
IV
|
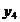
|
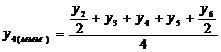
|
|
I
|
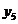
|
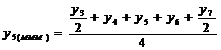
|
|
II
|
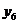
|
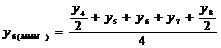
|
|
III
|
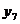
|
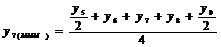
|
|
IV
|
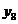
|
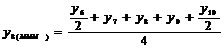
|
|
I
|
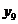
|
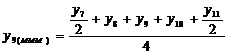
|
|
II
|
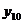
|
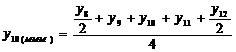
|
|
III
|
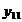
|
|
|
IV
|
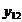
|
|
2. Ajustarea
analitica
Metoda analitica are un rol foarte omportant in procesul
de modelare econometrica a sriilor de timp, deoarece tendinta
fenomenului este stabilita cu ajutorul unei functii matematice care
evidentiaza mai bine evolutia datelor decat o reflecta
metodele analitice.
Tendinta de evolutie a activitatilor din sfera
cometului, turismului si serviciilor este stabilita, in general,
prin aceleasi functii prezentate prin metoda regresiei in capitolul 5
(Modele econometrice aplicate in analiza legaturilor stabilite in
activitatea de comert-turism-servicii). Apare o mica
diferenta in cazul functiilor numai in ceea ce priveste
variabila factoriala 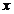 , care in cazul seriilor dinamice este inlocuita de
caracteristica timp notata cu
, care in cazul seriilor dinamice este inlocuita de
caracteristica timp notata cu 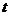 .
.
In raport cu forma de manifestare a
evolutiei datelor seriilor de timp se aplica una din cele doua
metode:
metoda trendului liniar;
metoda trendului neliniar
r
Metoda trendului liniar
In activitatea practica din comert,
turism sau servicii, de multe ori variatia in timp a datelor tinde spre o
evolutie de tip liniar.
Ecuatia de estimare a functiei liniare de trend este:
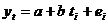
Pentru determinarea estimatorilor parametrilor 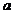 si
si 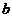 aplicam metoda
celor mai mici patrate
care conduce la sistemului de
ecuatii normale:
aplicam metoda
celor mai mici patrate
care conduce la sistemului de
ecuatii normale:
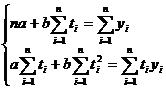 (5)
(5)
Determinarea estimatorilor parametrilor 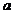 si
si 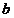 presupune rezolvarea
sistemului de ecuatii normale, numai ca de regula, deoarece
variabila timp reprezinta o serie de numere consecutive, se considera
ca originea este in centrul seriei, iar
presupune rezolvarea
sistemului de ecuatii normale, numai ca de regula, deoarece
variabila timp reprezinta o serie de numere consecutive, se considera
ca originea este in centrul seriei, iar 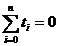 . Atunci, din sistemul de ecuatii normale (5) devine
. Atunci, din sistemul de ecuatii normale (5) devine
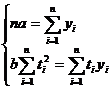 (6)
(6)
cu solutiile:
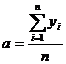
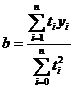 (7)
(7)
Observatii
Valorile variabilei timp ( 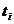 ) sunt numere intregi
) sunt numere intregi
Daca seria de timp este formata
dint-un numar par de termeni, atunci 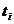 va
lua valorile: , -2, -1, 1, 2,.
va
lua valorile: , -2, -1, 1, 2,.
Daca seria de timp este formata
dint-un numar impar termeni, atunci 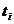 va
avea valorile: , -2, -1,
va
avea valorile: , -2, -1,
Exemplul 4 Considerand cunoscute datele privind numarul
sosirilor turistilor intr-o structura de primire turistica
pentru ultimii 11 ani (tabelul 3), se cere sa se stabileasca si
sa se interpreteze tendinta de evolutie prin aplicarea metodei
analitice adecvate.
Tabelul 3.
Numarul sosirilor turistilor la o structura de primire
Rezolvare
In vederea
stabilirii metodei de ajustare care poate fi aplicate, trebuie in primul rand
sa se realizeze o reprezentare grafica a evolutiei sosirilor
turistilor (figura 4).
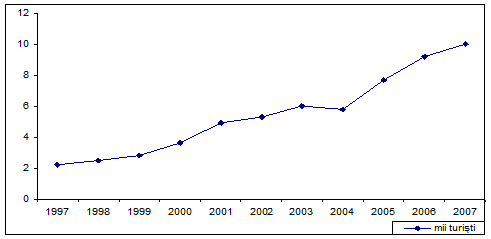
Figura 4. Evolutia
sosirilor turistilor in perioada 1997-2007
Graficul (corelograma) din figura 5 evidentiaza o evolutie a
numarului sosirilor turistilor care tinde spre liniaritate, ceea ce
impune aplicarea metodei trendului liniar.
Din sistemul de ecuatii normale
(6) unde 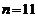 si tinand seama de
valorile numerice din tabelul 4 rezulta estimatorii parametrilor:
si tinand seama de
valorile numerice din tabelul 4 rezulta estimatorii parametrilor:
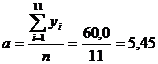
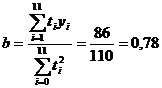
Deci, ecuatia de estimare a functiei liniare de trend va fi:
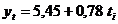
Tabelul 4. Algoritm
pentru aplicarea metodei trendului liniar
|
Anii
|
Nr. Sosiri turisti (mii)
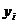
|
Valori
timp
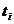
|
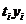
|
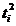
|
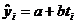
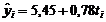
|
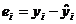
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
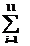
|
|
|
|
|
|
|
In seria de timp privind sosirile turistilor in respectiva strura
de primire turistica se observa ca, abaterile (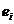 )de la tendinta medie sunt relativ mici. Cum
)de la tendinta medie sunt relativ mici. Cum 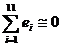 , deci
, deci 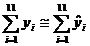 , inseamna ca metoda trendului liniar
evidentiaza bine tendinta de evolutie de tip liniar a
numarului sosirilor turistilor.
, inseamna ca metoda trendului liniar
evidentiaza bine tendinta de evolutie de tip liniar a
numarului sosirilor turistilor.
r
Metoda trendului neliniar
Modelele econometrice aplicate in raport cu metodele trendului neliniar
urmeaza aceeasi metodologie ca in cazul metodei trendului liniar
numai ca, ecuatiile de estimare, sistemele de ecuatii normale
si relatiile parametrilor depind de tipul modelului neliniar, dupa
cum se prezinta in tabelul 5
Tabelul 5 Liniarizarea
unor sisteme neliniare
|
Tipuri de modele
|
Ecuatia de estimare a functiei de trend
|
Sistemul de ecuatii normalesi
parametrii 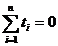
| |
|
Modele de trend
clasice
|
Parabolic
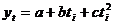
|
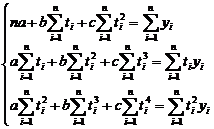
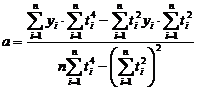
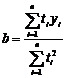
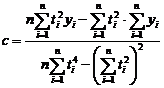
| |
|
EXPONENTIAL
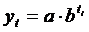
|
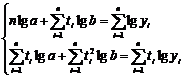
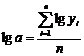
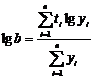
|
|
Modele de trend
particulare
|
EXPONENTIAL
MODIFICAT
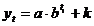 unde unde
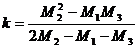
Seria este impartita in trei parti egale (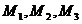 ); );
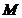 - media selectionata pentru fiecare perioada
de timp - media selectionata pentru fiecare perioada
de timp
|
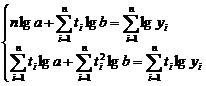
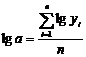
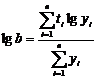
|
Logistic
generalizat
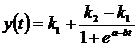
|
se calculeaza
marimile inverse ale lui 
se impart termenii
seriei, in ordine cronologica, in trei parti egale, fiecare
parte cuprinzand cate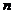 temeni; temeni;
se calculeaza,
pentru fiecare din cele trei parti, sume partiale ale
intervalelor valorilor lui  , respectiv , respectiv 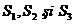 pe baza
relatiilor: pe baza
relatiilor:
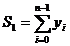 ; ; 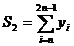 ; ; 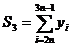
se calculeaza
diferentele dintre sumele partiale:
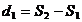 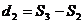
se efectueaza
calculul parametrilor:
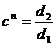 , respectiv , respectiv 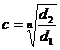
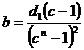 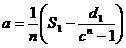
se afla valorile
variabilei 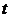 fata
deorigine, care corespunde primului termen al seriei; fata
deorigine, care corespunde primului termen al seriei;
se calculeaza
marimile inverse ale lui  , pe baza valorilor paramerilor si in raport cu , pe baza valorilor paramerilor si in raport cu 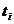
|
Logistic
clasic
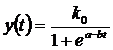
|
|
Logistic
particularizat
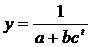
|
|
Curba
Gompez
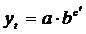
|
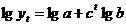
se imparte seria, in
ordine cronologica, in trei parti egale cu un numar de 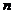 temeni; temeni;
se calculeaza,
pentru fiecare din cele trei parti, suma logaritmilor valorilor
observate, respectiv 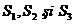 ; ;
se calculeaza
diferentele dintre sumele partiale:
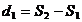 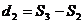
se efectueaza
calculul parametrilor:
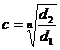 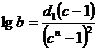
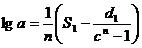
|
| | | | |