Indicatori
statistici ai masurarilor. funcTii matlab pentru calcule
statistice
1. OBIECTIVELE LUCRARII
Studiul functiilor MATLAB pentru
calcule statistice. Aplicatii.
2. BREVIAR TEORETIC
Functiile uzuale MATLAB folosite
pentru calcule statistice sunt urmatoarele
1) cumsum(x,dim) - calculeaza suma
cumulata a elementelor vectorului x
de dimensiune dim.
Pentru o matrice rezultatul este tot o matrice cu
dimensiunile lui x si contine suma cumulata pentru fiecare
coloana.
Exemplu
Pentru X=
cumsum(X,1);
are ca rezultat matricea [1 2 3;2 4
6]
iar cumsum(X,2);
are ca rezultat vectorul [1 3 6;1 3 6];
2) cumprod(x,dim) - calculeaza
produsul cumulat al elementelor vectorului x.
Pentru x matrice rezultatul este tot
o matrice cu dimensiunile lui x si
contine produsul cumulat al fiecarei coloane.
Exemplu
cumprod(x,1)
are ca rezultat matricea [1 2 3; 1 4 9]
cumprod(x,2)
are ca rezultat matricea [1 2 6; 1 2 6].
3) corrcoef(x) - calculeaza o
matrice pentru coeficienti de corelatie pentru un vector x, in care fiecare linie a matricei este o
observatie, iar fiecare linie este o variabila.
corrcoef(x,y,) , unde x si y sunt
vectori coloana este acelasi lucru cu a scrie corrcoef([x,y
Coeficientii de corelatie ai datelor se
folosesc pentru a stabili daca intre doua seturi de date inregistrate
in 2 vectori diferiti exista o dependenta liniara.
Exemplu
x=[1 2 3; 2 7 5;
3 5 8]
a=[1 2 3;4 5 6; 7 8 9];
r=corrcoef(x)
are ca rezultat
r=
0.5960 0.9934
1.0000 0.5000
0.9934 0.5000 1.0000
iar
r=corrcoef(a,x)
are ca rezultat
r=
0.7614
0.7614 1.0000
4) cov(x) - daca x este un
vector functia intoarce varianta acestuia. Daca x este o matrice
cu liniile observatii si coloanele variabile aceasta functie va
returna o matrice de covarianta
Exemplu
cov(x) pentru matricea de mai sus va returna
1.5000 2.5000
6.3333 3.1667
3.1667 6.3333
5) diff(x) - diferenta dintre
numerele succesive.
Pentru un vector cu elementele x1 . xn
diferenta este tot un vector calculat astfel [x2 - x1
. xn - xn-1], iar pentru o matrice se face diferenta
dintre liniile succesive.
Exemplu
a= [2 4 3 5 1 7];
diff(a) = [2 -1 2 -4 6]
x=[1 2 3; 2 7 5; 3 5 8];
diff(x) = [1 5 2;1 -2 3]
6)n=hist(y) - imparte elementele lui
y in 10 intervale egale si returneaza numarul de elemente din
fiecare interval. Daca y este o matrice hist va lucra in josul coloanelor.
Hist() - fara
argumente produce o histograma, conform exemplelor prezemtate in figura
4.1 si figura 4.2.
Exemplul 1
Secventa de program
a= [2 4 3 5 1 7]
hist(a)
produce reprezentarea
grafica din figura 4.1.
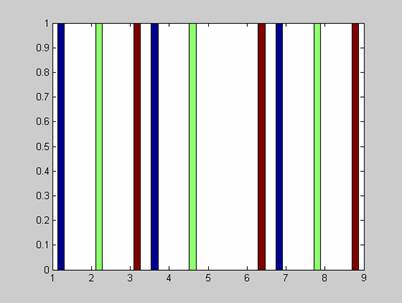
Fig.4.1.
Histograma corespunzatoare exemplului 1
Exemplul2
Secventa de program
x=[1 2 3; 2 7 5; 3 5 8];
hist(x).
produce histograma din
figura 4.2.
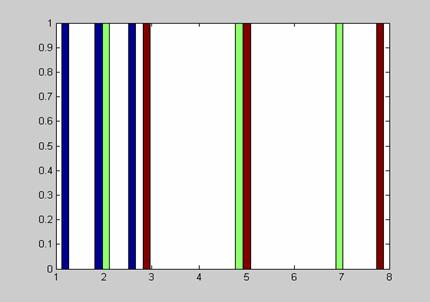
Fig.4.2. Histograma corespunzatoare
exemplului 2
7) max(x), min(x) - returneaza valoare
maxima, respectiv minima a componentelor vectorului x.
Daca x este matrice returneaza intr-un vector maximul/minimul
de pe fiecare coloana.
Exemplu
a= [2 4 3 5 1 7] ;
min(a)= 1
x=[1 2 3; 2 7 5; 3 5 8];
max(x)=
8) mean(x) - returneaza valoarea medie a
unui set de date dintr-un vector x. Daca datele sunt elementele unei
matrice, valoarea medie este continuta de un vector care are
elementele valorile medii ale fiecarei coloane.
Exemplu
a= [2 4 3 5 1 7] ;
x=[1 2 3; 2 7 5; 3 5 8];
mean(a)=3,667
mean(x)= 2.0000 4.6667 5.3333
9) prod(x) - calculeaza
produsul elementelor unui vector, iar pentru o matrice rezultatul este un
vector care are ca elementele produsul de pe fiecare coloana a matricei.
Exemplu
a= [2 4 3 5 1 7];
x=[1 2 3; 2 7 5; 3 5 8];
prod(a)=840
prod(x)= 120
sort(x) - sorteaza
elementele unui vector sau matrice in ordine crescatoare (la matrice
sortarea se face pe fiecare coloana)
Exemplu
a= [2 4 3 5 1 7] ;
x=[1 2 3; 2 7 5; 3 5 8];
sort(a)= 1 2 3 4 5 7]
sort(x)= 1 2 3; 2 5 5; 3 7 8]
11) std(x) - calculeaza
abaterea standard.
Exemplu
a= [2 4 3 5 1 7] ;
x=[1 2 3; 2 7 5; 3 5 8];
std(a)=
std(x)= 2.5166 2.5166]
12) sum(x) - calculeaza suma
elementelor unui vector, iar pentru o matrice se obtine un vector cu
elemente ce au valoarea egala cu suma de pe fiecare coloana.
Exemplu
a= [2 4 3 5 1 7] ;
x=[1 2 3; 2 7 5; 3 5 8];
sum(a)=22
sum(x)= 14 16]
13) trapz(x) - calculeaza
integrala folosind metoda trapezelor luand in considerare si
spatiile.
Exemplu
a= [2 4 3 5 1 7] ;
x=[1 2 3; 2 7 5; 3 5 8];
trapz(a)=
trapz(x)=[4 10,5 10,5]
14) table1(tab,x0) - returneaza un
tabel cu interpolarele liniare ale liniilor
din tabelul tab.
Exemplu
a= [2 4 3 ; 5 1 7] ;
r=table1(a,3)= 4,333]
y=interpft(x,n) - returneaza
vectorul y cu lungimea n obtinut prin interpolarea lui x prin metoda
transformatei Fourier.
Daca x este o matrice interpolarea se face pe
fiecare coloana.
Exemplu
a= [2 4 3 ; 5 1 7] ;
y=interpft(a,2)= 2 4 3
5 1 7]
16) polyfit(x,y,n) - aproximeaza un
set de date cu un polinom P(x) de gradul
n.
Exemplu
a=[2
4 3;5 1 7];
b=[1 4 2; 1 5 7];
polyfit(a,b,3)
ans =[-0.0109 0.5471 -3.3582 7.192
17) griddata(x,y,z,xi,yi) -
interpoleaza prin metoda distantei inverse valoarea unei functii
de doua variabile x, y
3. MODUL DE LUCRU
3.1. Probleme rezolvate
Fie doi vectori x=[-2 -1 0 2 4 ]; y=[-15 -3 2
3 10]; Sa se aplice o procedura de regresie liniara celor doi vectori
si sa se reprezinte grafic rezultatul obtinut.
Rezolvare
x=[-2 -1 0 2 4
];
y=[-15 -3 2 3
10];
coef=polyfit(x,y,1);
xn=-2:1:4;
y1=polyval(coef,xn)
plot(xn,y1,'r');
coef =
3.4828 -2.6897
y1 =-9.6552 -6.1724 -2.6897 0.7931 4.2759 7.7586 11.2414
Reprezentarea grafica a dreptei obtinute
in urma aplicarii procedurii de regresie liniara este cea din figura
4.3.
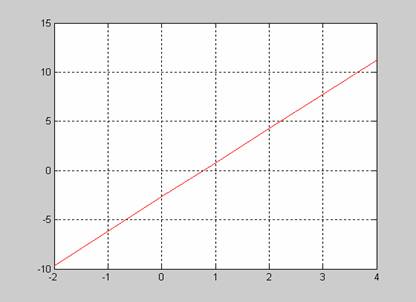
Fig.4.3.
Regresie liniara
2. Pentru un servomotor cu
pozitioner s-au obtinut datele experimentale din tabelul
urmator:
Sa se traseze
caracteristica statica a servomotorului cu pozitioner .
Rezolvare
p=[0.2 0.3 0.4
0.5 0.6 0.7 0.8 0.9 1];
h1=[0 5 12 16 21
27 32 32 32];
table1(p,0.2);
plot(p,h1);
grid on;
ylabel('H[mm]');
xlabel('presiunea
[bar]');
title('CARACTERISTICA STATICA A SERVOMOTORULUI CU POZITIONER');
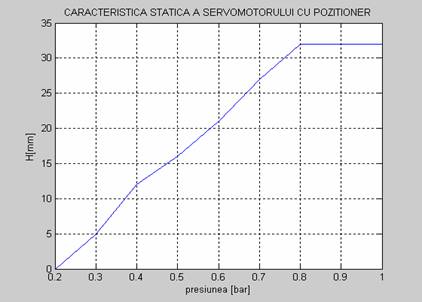
Fig.4.4. Caracteristica
statica a servomotorului cu pozitioner
3.2. Probleme propuse
1. Sa se
determine minimul si maximul vectorului V si matricei M, unde :
V=[1 3 -9 0]
M=[1 2 3; -4 0 9; 13 7 -10]
2 Sa se sorteze
matricele A si B de forma:
A
B=[7 2 -5 4 -1; 5 8 1 -6 -4; 2 0 -3 6 9]
3. Sa se
realizeze prin interpolare graficul unei functii stiind ca acesta
contine punctele A(1,1), B(2,3), C(2.5,5), D(4,6), E(6,10).
Fie vectorii
x=[-2
-1 0 2 4 ]; y=[-15 -3 2 3 10].
Sa se
aplice o procedura de regresie
liniara celor doi vectori.
5. Fie matricea A, de forma
A=
Sa se calculeze:
- suma cumulata;
- produsul
cumulat;
- produsul
si suma elementelor;
- sa se
sorteze mai intai dupa linii si apoi dupa coloane.
Sa se
reprezinte grafic histograma corespunzatoare.





