CENTRUL DE GREUTATE AL CORPURILOR OMOGENE
In
mecanica, corpul rigid se admite ca fiind un continuu material
nedeformabil, adica orice element de volum are masa iar
distantele dintre puncte raman nemodificate, indiferent de
solicitarile la care este supus corpul. Pentru a stabili o
legatura cu rezultatele obtinute in cazul sistemelor de n puncte materiale se considera
corpul divizat in volume elementare DVi,
de mase Dmi
Vectorul
de pozitie al centrului de masa este definit, conform relatiei
(3.4) cu conditia discretizarii la limita a maselor elementare.
Cand 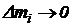 , sumele definite de (3.4) devin integrale, definite pe
domeniul (D), ocupat de corp.
, sumele definite de (3.4) devin integrale, definite pe
domeniul (D), ocupat de corp.
 (3.12)
(3.12)
Domeniul (D) se va nota cu: (V), in cazul blocurilor
- corpuri cu trei dimensiuni, (A), in
cazul placilor - corpuri cu
doua dimensiuni, a treia fiind neglijabila in raport cu celelalte
doua si (l), in cazul barelor - corpuri cu o singura
dimensiune, celelalte doua fiind neglijabile in raport cu prima.
Corpul omogen este corpul a carui densitate este
aceasi in toate punctele sale. Cum densitatea
sau masa specifica a corpului
(blocului) este definita prin raportul dintre masa corespunzatoare
si volumul elementar,
 (3.13)
(3.13)
vectorul de pozitie al centrului de masa
al blocului omogen este:
 (3.14)
(3.14)
ale carui coordonate sunt:
 (3.15)
(3.15)
In cazul placilor se
poate defini, in mod analog, densitatea
superficiala .
 (3.16)
(3.16)
Vectorul de pozitie al centrului de masa al
placii omogene este:
 (3.17)
(3.17)
ale carui coordonate sunt:
 (3.18)
(3.18)
In cazul barelor se
defineste densitatea liniara:
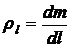 (3.19)
(3.19)
Vectorul de pozitie
al centrului de masa al barei omogene are expresia:
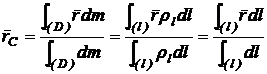 (3.20)
(3.20)
ale carui coordonate sunt:
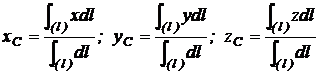 (3.21)
(3.21)



 (3.14)
(3.14) (3.15)
(3.15) (3.17)
(3.17) (3.18)
(3.18)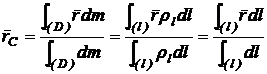 (3.20)
(3.20)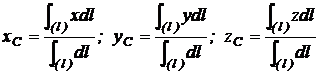 (3.21)
(3.21)