Compunerea oscilatiilor paralele si de aceeasi frecventa

Compunerea oscilatiilor paralele si de aceeasi frecventa

Un acelasi punct material poate fi supus simultan la doua miscari oscilatorii armonice. Fie doua astfel de miscari care au aceeasi frecventa (pulsatie), dar amplitudini si faze diferite si ale caror legi de miscare sunt:

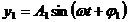
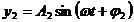  (1.16)

Se poate demonstra ca prin compunerea celor doua miscari se obtine tot o miscare oscilatorie armonica, adica legea miscarii rezultante este:

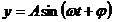    (1.17)

unde amplitudinea se calculeaza cu formula: 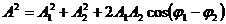, (1.18)

iar faza initiala se obtine din:

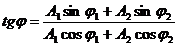    (1.19)

Cazuri particulare ale compunerii oscilatiilor:

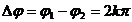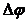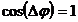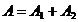1. Daca , k=0,1,2,3,.  adica diferenta de faza este un numar par de π, atunci si din formula amplitudinii rezultante obtinem: . Aceste oscilatii se intaresc reciproc si se numesc oscilatii in concordanta
   de faza.
2. Daca , k=0,1,2,3,.  adica diferenta de faza 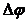este un numar impar de π, atunci 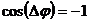si din formula amplitudinii rezultante obtinem: . Aceste oscilatii sunt in opozitie de faza, iar daca , deci oscilatiile se sting.
3. Daca 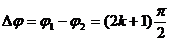,  k=0,1,2,3,. adica diferenta de faza 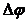este un numar impar de π/2, atunci si din formula amplitudinii rezultante obtinem: 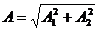. Aceste oscilatii se numesc la cuadratura sau sfert.