ESTIMATORI DE PRECIZIE SUPLIMENTARI
LA PRELUCRAREA MASURATORILOR EFECTUATE IN RETELE PLANIMETRICE GEODEZICE CU METODA OBSERVATIILOR INDIRECTE

 (9)
(9)
RETELE PLANIMETRICE
P(x,y)
N -matricea sistemelor de ecuatii normaleI=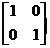 (12)
(12)
N =Q
=Q
N *N=I
*N=I
|
1
|
2
|
|
R
|
|
u
|
|
x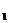
|
y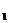
|
x2
|
y2
|
|
|
xR
|
yR
|
|
|
xu
|
yu
|
|
1
|
x1
|
Qx1x1
|
Qx1y1
|
Qx1x2
|
Qx1y2
|
|
|
Qx1xR
|
Qx1yR
|
|
|
Qx1xu
|
Qx1yu
|
|
y1
|
Qy1x1
|
Qy1y1
|
Qy1x2
|
Qy1y2
|
|
|
Qy1xR
|
Qy1yR
|
|
|
Qy1xu
|
Qy1yu
|
|
2
|
x2
|
Qx2x1
|
Qx2y1
|
Qx2x2
|
Qx2y2
|
|
|
Qx2xR
|
Qx2yR
|
|
|
Qx2xu
|
Qx2yu
|
|
y2
|
Qy2x1
|
Qy2y1
|
Qy2x2
|
Qy2y2
|
|
|
Qy2xR
|
Qy2yR
|
|
|
Qy2xu
|
Qy2yu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R
|
xR
|
QxRx1
|
QxRy1
|
QxRx2
|
QxRy2
|
|
|
QxRxR
|
QxRyR
|
|
|
QxRxu
|
QxRyu
|
|
yR
|
QyRx1
|
QyRy1
|
QyRx2
|
QyRy2
|
|
|
QyRxR
|
QyRyR
|
|
|
QyRxu
|
QyRyu
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u
|
xu
|
Qxux1
|
Qxuy1
|
Qxux2
|
Qxuy2
|
|
|
QxuxR
|
QxuyR
|
|
|
Qxuxu
|
Qxuyu
|
|
yu
|
qyux1
|
Qyuy1
|
Qyux2
|
Qyuy2
|
|
|
QyuXR
|
QyuyR
|
|
|
Qyuxu
|
Qyuyu
|
N =Qxx=n puncte noi
=Qxx=n puncte noi
Pt.fiecare punct nou se adauga 2 coloane
EVALUAREA
PRECIZIEI IN RETELELE PLANIMETRICE
1.ERORILE
INDIVIDUALE - relativ la punctul de la mijlocul retelei R
 ,unde So - abaterea standard a unitatii de pondere
,unde So - abaterea standard a unitatii de pondere

 ,unde[pvv]se va determina cu 2 procedee,n=nr de masuratori,u = nr de
necunoscute
,unde[pvv]se va determina cu 2 procedee,n=nr de masuratori,u = nr de
necunoscute
Helmert-abatere standard totala(a introdus
notiunea)
Pt.pct R abaterea se calculeaza cu relatia
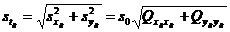 (6`)
(6`)
Generalizarea formulei 6 ne conduce la
determinarea abaterii stand.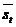 care este un indicator de precizie pt
toata reteaua planimetrica
care este un indicator de precizie pt
toata reteaua planimetrica
 (7`)
(7`)
urma Q
 (13)
(13)
2.In fiecare punct nou se determina elipsele erorilor
In pct R de la mij retelei
-semiaxele elipsei
 unde λ1si λ2se calculeaza cu relatia (10)
unde λ1si λ2se calculeaza cu relatia (10)
 (10`)
(10`)
Orientarea axei mari a elipsei,adika unghiul format de axa mare a
elipsei cu axa x in pct R este notata θ care se calculeaza cu (11`)
care se calculeaza cu (11`)

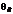
 .(11`)
.(11`)
Elipsa erorilor ne da domeniul de incredere in
jurul punctului R.
Coeficientii de pondere
necesari in relatiile(3`) si (4`)pana la (11`)se extrag din matricea inversa
N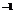 =Q
=Q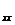
Denumiri folosite:
a)coef de pondere de forma:
QxRxR si
QyRyR se numesc coef de pondere patratici.Acestia se gasesc pe diagonala
matricei N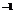 =Q
=Q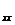
b)Coef de forma QxRyR se numesc coaf de pondere
dreptunghiulari si intervin la fiecare pct nou pe diagonala
Coef de pondere patratici de forma Qxx se
calculeaza k la lucrarea 4
Coef de pondere dreptunghiulari se calculeaza
analog,dar se fac produsele pe diagonala
tab 7
|
Qxx
|
Qyy
|
|
|
|
|
x
|
|
linie rosie
|
x
|
|
In
algebra s-a folositnotiunea de sisteme echivalente si anume:''2 sisteme de ec
se numesc echivalente daca au aceleasi solutii''
In
geodezie si TPD se folosesc 3 sisteme de ecuatii de echivalenta a unor sisteme
de ecuatii de corectii descoperite de catre Schveiber cunoscute si sub numele
de regulile Schveiber de echivalenta.Aceste reguli de echivalenta au 2
proprietati:
a.se
pot aplica extrem de simplu(fiecare in anumite situatii)
b.conduc
la micsorari importante ale volumului de calcul
De
fiecare data va rezulta un alt sistem de ec.de corectii echivalent cu sist
initial. La fiecare regula treb retinut>: 1.cand se poate aplica regula
respectiva, 2.cum se aplica regula
Sub.
2 Situatia 1 de echivalenta. Se
considera urmatorul sistem de ecuatii ale corectiilor:
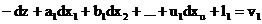 pondere p1;
pondere p1;
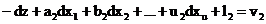 pondere p2;
pondere p2;
.
 pondere pn.(1)
pondere pn.(1)
Obs!..La fel ca in oricare sistem de corectii n>u(2)
In toate ec intervine nec
dz, care in toate ec are coef -1.
n>u+1. Ac.este conditia in care se poate
aplica reg1 de echiv a lui Schreiber.
Se va dem. ca sist (1)e echiv cu urm sist de ec.
Se observa ca necunoscuta dz are
coeficientul -1 in toate ecuatiile. Sistemul
(6.13) poate fi inlocuit printr-un sistem echivalent (6.14), care are un
numar de n+1 ecuatii, insa din care lipseste necunoscuta
dz:
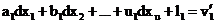 pondere p1;
pondere p1;
 pondere p2;
pondere p2;
.
. .
 pondere pn;
pondere pn;
 pondere
pondere 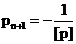 .(3)
.(3)
Ultima ecuatie a sistemului (3) este
denumita ecuatie suma.
Pentru demonstrarea echivalentei urmarite, se formeaza sistemul
de ecuatii normale corespunzator sistemului (6.13):
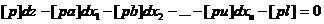

. .
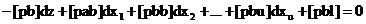
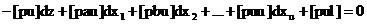 .(5)
.(5)
Se deduce necunoscuta
dz din prima ecuatie normala:

si se introduce in celelalte ecuatii.
In acest fel se obtine:

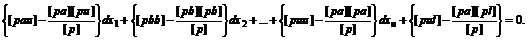 (7)
(7)
Formand direct ecuatiile normale ale
sistemului (1) vor rezulta aceleasi ecuatii (7), ceea ce
demonstreaza echivalenta cautata.
Sist (7) este sistemul de ec normale obtinut din
sist de ec de corectii(1) dupa ce s-a obtinut din sist de ec de corectii, dupa
ce s-a eliminat nec dz. Si acest sist indepl cele 3propr specifice sist lor de
ec normale:
a).sist. este patrata;dar spre deoseb. de (5) are
cu dimensiune mai putin:cu linii si cu coloane.
b)este simetrie fata de diagonala principala
c)termeni de pe diagonala sunt pozitivi
Dupa determinarea (calcularea) necunoscutelor ce
intervin in(7):
dx1 dx2 dxn cu metoda Gauss(eliminari
succcesive se determina(calc.)
Datorita regulii 1 de echiv nu se mai rez sist de
ec normale(5) ci se rez.(7), care are o nec mai putin.
Sub.
3.Situatia 2 de echivalenta. Fie
un sistem de k ecuatii ale corectiilor, cu aceiasi
coeficienti ai necunoscutelor x, insa cu termenii liberi
diferiti. Ecuatiile au ponderi diferite.
 pondere p1;
pondere p1;
 pondere p2;
pondere p2;
. . . (1)
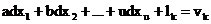 pondere pk.
pondere pk.
Acest sistem este echivalent cu urmatoarea
ecuatie:
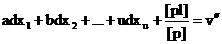 pondere
pondere 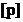 , (2) (6.19)
, (2) (6.19)
in care termenul liber este media ponderata
a termenilor liberi din sistemul (6.18) iar ponderea sa este egala cu suma
ponderilor ecuatiilor (6.18).
Intr-adevar,
sistemului (6.18) ii corespunde urmatorul sistem de ecuatii normale:
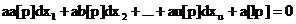
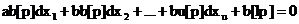 ; (6.20)
; (6.20)
 n>u (5)
n>u (5)
Nota:Nu se poate forma
un sist de ecuatii normale dintr-o singura ecuatie de corectie.Lucrurile
trebuie intelese in felul urm:sis 1 este o componenta a unui sist de ecuatii
normale mult mult mai mare in care se respecta regula 5.Aceasta situatie de
echivalenta inseamna ca in loc sa lucrezi cu (1) inlocuiesc sistemul cu ac ec
(2)
Si la aceasta regula
de echivalenta se respecta regula ca poate fi aplicata cu usurinta ec (2).
Ecuatiei (6.19)
ii corespunde acelasi sistem de ecuatii normale.
Obs. Este de observat ca aceasta demonstratie
este posibila numai in situatia in care numarul total al ecuatiilor de corectii ramane mai
mare ca numarul necunoscutelor. Aceasta presupune ca situatia
examinata se intalneste intr-un cadru mai general, intr-o prelucrare
in care intervin mult mai multe
ecuatii decat cele avute in vedere. O formulare mai exacta a cestei
reguli ar fi: un sistem particular de ecuatii de corectii de forma
(6.18), care este parte componenta a unui sistem mult mai mare, poate fi
inlocuit de ecuatia (6.19.) inainte de trecerea la sistemul de
ecuatii normale corespondent deoarece contributia
acestora este aceeasi.
Sub. 4.Regula 3 de
echivalenta pt 2 sist de ecuatii de corectii
Pp ca avem intr-un sistem mare de ecuatii o ecuatie de urm forma:
vk=adx+bdy+cdz+l;p (1)
Ec (1) este adusa la ponderea=1;se inmulteste cu √p
vk'=√padx+√pbdy+√pcdz+√pl;p'=1 (2)
Dem:din ecuatia (1) rezulta acelasi sist ca din ecuatia (2)
Contributia ec (1) la un sist mul mai mare
aapdx+abpdy+acpdz+alp=0
abpdx+bbpdy+bcpdz+blp=0 (3)
acpdx+bcpdy+ccpdz+clp=0
Aceeasi contributie o are si ecuatia (2)
Obs:De multe ori ecuatia de corectie trebuie impartite cu o constanta
k
v"'=(a/k)dx+(b/k)dy+(c/k)dz+l/k;p"'=pk2 (4)
Din (4) se obtine (3)





