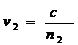Fotoelasticitatea
Printre mijloacele cele mai folosite in
analiza experimentala a starii de tensiune se numara si
fotoelasticitatea. Fotoelasticitatea, ca si fotoplasticitatea sau
fotoviscoelasticitatea, este una din metodele de investigatie ale
fotomecanicii, bazata pe interpretarea datelor rezultate din masurarea birefrigerentei accidentale. Avind la
baza principiile opticii experimentale si teoria matematica a
elasticitatii, fotoelasticitatea s-a remarcat de la inceput ca o tehnica
experimentala simpla si cu posibilitati largi de aplicare in analiza starii de
tensiuni si deformatii. Spre deosebire de alte metode tenso-metrice (mecanice,
optice sau electrice), care furnizeaza informatii
in puncte discrete, fotoelasticitatea permite obtinerea unui tablou
complet al cimpului de tensiune, dind astfel posibilitatea determinarii starii
de tensiune (in marime si directie) in orice punct. Avind o mare utilitate practica in determinarea concentrarilor
de tensiuni si a starilor de tensiune in piesele cu forme geometrice
complicate, fotoelasticitatea a devenit o unealta de pret pentru ingineri in
proiectarea rationala a organelor de masini si elementelor structurale.
1.1. NOTIUNI
DE OPTICA GENERALA
1.1.1. NATURA
LUMINII
Dupa cum este cunoscut, pentru a
explica comportarea energiei radiate,
fizica moderna admite ca lumina are o dubla natura : corpusculara si ondulatorie. Potrivit conceptiei corpusculare,
lumina este considerata ca un flux de particule foarte mici proiectate
in toate directiile de la sursa. Conceptul
lui Maxwell privind natura ondulatorie [1], presupune ca lumina este o perturbatie a cimpului
electromagnetic reprezentata prin doi
vectori, unul electric si celalalt magnetic, perpendiculari intre ei si pe directia de propagare. Comportarea luminii poate fi
studiata considerind doar unul din cei doi vectori, care se va numi
vector luminos. In cele ce urmeaza, pentru a usura intelegerea efectului
fotoelastic se presupune ca lumina obisnuita
reprezinta o perturbatie a cimpului electromagnetic in care particulele vibreaza in plane ce contin
direcfia de propagare. In aceasta
schema de vizualizare a fenomenului optic, vectorul luminos reprezinta directia de vibratie a acestor
particule si amplitudinea vibratiei la
un moment dat.
In cazul luminii ordinare (cum este
lumina emisa de un bec), vectorul luminos
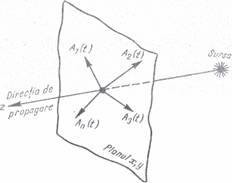
poate fi considerat ca fiind compus dintr-un numar arbitrar de vibratii transversale reprezentate prin vectorii A (t),A (t),, An(f); (fig. 4.1).
 Lumina conceputa ca o perturbatie electromagnetica, se
propaga cu o anumita viteza care depinde de
densitatea mediului. Astfel in vid lumina are o viteza maxima de propagare c = 2,997-10s m/s, in
timp ce in oricare alt mediu
transparent viteza este mai mica. Raportul dintre viteza luminii in vid c si viteza de propagare vi printr-un
mediu oarecare, poarta numele
de indice absolut de refractiie ni ni
Lumina conceputa ca o perturbatie electromagnetica, se
propaga cu o anumita viteza care depinde de
densitatea mediului. Astfel in vid lumina are o viteza maxima de propagare c = 2,997-10s m/s, in
timp ce in oricare alt mediu
transparent viteza este mai mica. Raportul dintre viteza luminii in vid c si viteza de propagare vi printr-un
mediu oarecare, poarta numele
de indice absolut de refractiie ni ni 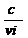 (1.1)
(1.1)
Daca notam cu n c/v1 si n2=c/v2 indicii absolute de
refractie pentru doua medii diferite,se poate defini indicele relativ de refractie
n 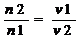 (1.2
(1.2
Efectul fiziologic produs de o raza de lumina care cade pe ochiul unui
observator, depinde de lungimea de unda si amplitudinea radiafiei luminoase. Astfel culoarea observata este
determinata de lungimea de unda λ, in timp ce stralucirea depinde numai de
amplitudinea radiatiei. luminoase. Este de
remarcat ca ochiul omenesc sesizeaza culori corespunzatoare unor lungimi de unda care variaza intre λ = 4·1 m (violet) si λ = 7,2·10-7 m(rosu inchis). Lumina monocromatica sau
omogena este compusa din vibratii transversale a caror lungime de unda este
aproximativ aceeasi sau variaza intr-o banda foarte ingusta de lungimi de unda.
MISCAREA ARMONICA
Un punct
material executa o miScare armonica simpla, cand se misca pe o dreapta,
avind in orice moment aceleratia indreptata spre
un punct fix aflat pe traiectoria sa si direct proportionala cu distanta fata de acest punct (fig. 4.2). Ecuatia diferentila care guverneaza acest tip de miscare
este
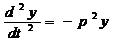 unde t=timp,y=distanta la momentul
t fata de punctual fix, p=pulsatia miscarii,solutia generala fiind :
unde t=timp,y=distanta la momentul
t fata de punctual fix, p=pulsatia miscarii,solutia generala fiind :
y=α sin
(pt+φ) (1.3)
Aceasta reprezinta ecuatia miscarii armonice
simple in care α=elongatia maxima sau amplitudine,iar φ =diferenta de faza unghiulara.In cazul in care
diferenta de faza unghiulara φ =0,ecuatia
de miscare devine y=α sin pt sau y= α sin 2Π 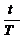 (1.4)
(1.4)
Miscarea
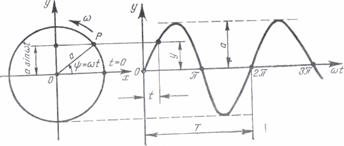
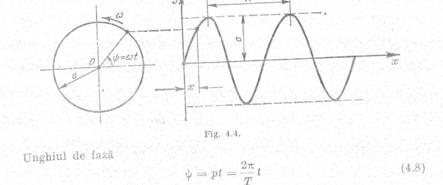
armonica simpla poate fi sugerata S cu ajutorul miscarii circulare. Sa consideram un punct material P care
se miSa pe un cerc raza a cu o viteza unghiulara constanta ω (fig. 4.3). Proiectia
punctului P pe diametrul vertical executa o miscare armonica simpla
reprezentata prin urmatoarea ecuatie y= a sin ωt,unde:
ωt=ψ=unghiul de faza sau faza unghiulara
Doua miscari armonice simple care au loc in plane
perpendiculare,avand aceeasi perioada si o diferenta de faza φ intre ele
se reprezinta prin ecuatia
y=b sin (pt+ φ) (1.5)
Figura 4.3
Prin compunerea celor doua
miscari se obtine o miscare rezultanta.Ecuatia traiectoriei miscarii rezultante
se obtine eliminand parametrul t intre cele doua relatii:
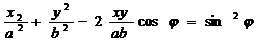 (1.6)
(1.6)
Aceasta ecuatie reprezinta o
elipsa ,deci se vor compune doua miscari armonice simple pe doua plane
perpendiculare(diferenta de faza φ are o miscare circulara):
a)Cele doua miscari au aceeasi amplitudine a=b si diferenta
de faza φ=±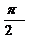 astfel
avem: x˛+y˛=a˛=b˛;
astfel
avem: x˛+y˛=a˛=b˛;
b)Cele doua miscari au o diferenta de faza φ=0,astfel
ca ecuatia (1.6) va deveni:
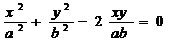 sau (xb-ya) ˛=0
sau (xb-ya) ˛=0
Rezultanta in
acest caz este o miscare rectilinie pe o directie care trece prin cadranele unu
si trei ale cercului trigonometric.
1.1.3 UNDE ARMONICE SIMPLE
Lumina conceputa ca o perturbatie a
cimpului electromagnetic, as.a cum s-a
vazut, se propaga prin mediile transparente sub forma unor unde. Pentru
simplificare, se va considera o singura unda de
lumina, care poate fi asimilata cu o unda armonica simpla. In acest caz, pozitia diferitelor puncte aflate in miscare
pe axa x, este data la momentul t de
o sinusoida (fig. 4.4). Lungimea de unda , reprezinta distanta dintre doua puncte aflate in faza,
masurata in lungul axei x.Unda
luminoasa se propaga in lungul axei x cu viteza c= 2,997 ·108
m/s.Cunoscind viteza de propagare c,
lungimea de unda λ., se calculeaza cu relatia
λ=cT (1.7)
Corespunde unui punct situate pe axa Ox la distanta
x=ct (1.9)
-unghiul de faza ψ poate fi exprimat in functie de x si de lungimea de unda λ
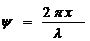 (1.10)
(1.10)
Cand undele se vor deplasa in sensul pozitiv al axei
x,ecuatia acestor unde va deveni
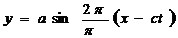 (1.11)
(1.11)
Se
considera o unda luminoasa care la momentul t= 0 este reprezentata prin sinusoida trasata cu linie
continua in fig. 4.5. Unda se deplaseaza in lungul axei x cu viteza c, potrivit
ecuatiei (1.11), astfel ca dupa un timp t = t, va ocupa pozitia desenata cu linie intrerupta.
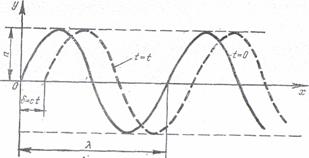 Figura
4.5
Figura
4.5
In noua pozitie unda se
gaseste deplasata fata de pozitia initiala cu distanta δ = ct, care
poarta numele de diferenta de faza liniara,iar intre diferenta de faza unghiulara si cea lineara exista urmatoarea relatie de legatura:
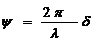 (1.12)
(1.12)
Tinind seama de (1.12), ecuatiile a doua unde care au intre
ele o diferenta de faza lineara δ, se
scriu astfel
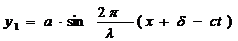
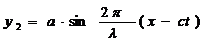 (1.13)
(1.13)
1.1.4.LUMINA POLARIZATA
In schematizarea fenomenului optic am
admis ca lumina reprezinta o perturbatie a campului electromagnetic, in care
particulele vibreaza in toate directiile cuprinse intr-un plan perpendicular pe
directia de propagare.Daca particulele aflate in miscare ,descriu traiectorii
bine determinate intr-un plan perpendicular pe directia de propagare.lumina
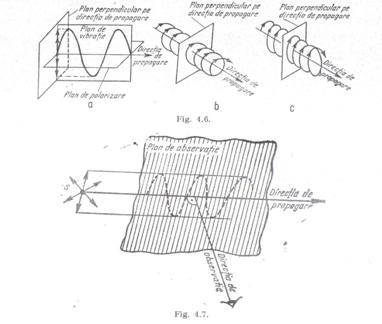
este polarizata.Cand traiectoria
miscarii este o dreapta perpendicular ape directia d epropagare ,lumina este
polarizata plan ca in fig 4.6a.Cand traiectoria miscarii este un cerc,lumina
este polarizata circular (fig 4.6 b),iar cand este o elipsa este polarizata
eliptic(fig 4.6.c).
Lumina obisnuita poate fi
polarizata prin mai multe metode:cu ajutorul campului electrostatic sau
electromagnetic,prin reflexii sau refractii successive ,la trecerea prin
anumite cristale ,sau cu ajutorul lamelor Polaroid.
Lumina
polarizata plan se mai poate obtine, observind dintr-o pozitie laterala un fascicul de lumina
obisnuita difuzata intr-un mediu transparent (fig. 4.7). In acest caz vor fi observate numai
acele componente ale vectorului
luminos care se proiecteaza in planul care contine directia de propagare si este perpendicular pe directia de observare.
Acest procedeu sta la baza unei noi tehnici
fotoelastice de analiza starii spatiale de tensiune.
1.1.5.TRANSMITEREA LUMINII PRIN MEDII
ANIZOTROPE
In mediile transparente izotrope,lumina
se propaga in toate directiile cu aceeasi viteza ,determinate de densitatea
mediului.Cand lumina obisnuita intalneste prin incidenta normala un mediu
transparent anizotrop,vectorul luminos se descompune in doua componente
particulare,polarizate plan.Acest fenomen este cunoscut sub numele de dubla
refractie sau birefrigerenta.Cele doua componente polarizate plan traverseaza
lama transparenta cu viteze diferite ,invers proportionale cu indiciide
refractie pe directiile respective 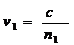 si
si