GHIDURI DE UNDA
Propagarea campului electromagnetic in
ghidurile de unda
Ghidul de unda este
destinat propagarii undelor electromagnetice. El are o structura plan paralela si
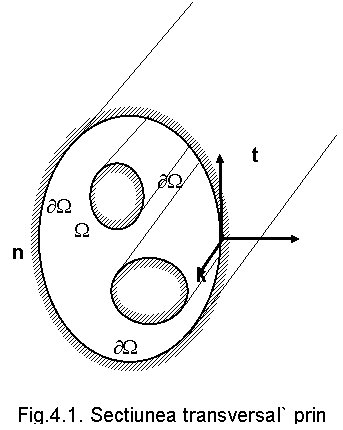
poate fi format din una sau mai multe armaturi (in fig.4.1, avem 3 armaturi)
Propagrea undei
electromagneice de-a lungul ghidului, in sensul axei oz, cu viteza v, inseamna regasirea valorilor
marimilor campului din sectiunea z si
timpul t, la sectiunea z+Dz si la timpul t+Dt, unde 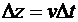 . De exemplu,
intensitatea campului electric, este de forma:
. De exemplu,
intensitatea campului electric, este de forma:  . Imediat se verifica:
. Imediat se verifica: 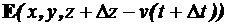 =
=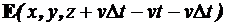 =
= in cazul regimului sinusoidal, avem:
in cazul regimului sinusoidal, avem:
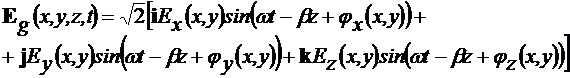
unde, pentru mai multa precizie, 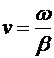 este numita viteza de
faza, marimea
este numita viteza de
faza, marimea 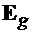 regasindu-si faza la
regasindu-si faza la 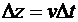 . Imaginea in complex este:
. Imaginea in complex este:
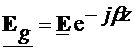 (4.1)
(4.1)
unde:

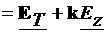 (4.2)
(4.2)
 si
si 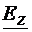 sunt componentele
transversala si longitudinala ale lui E.
sunt componentele
transversala si longitudinala ale lui E.
Este util sa determinam
expresiile operatorilor div si rot pentru componentele transversala si
longitudinala:
 (4.3)
(4.3)

 (4.4)
(4.4)
2.
Ecuatiile campului electromagnetic, pe componente longitudinale si transversale
|inand cont de (4.4),
legea inductiei electromagnetice devine:
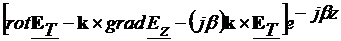 =
=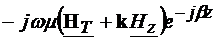
Egaland componentele transversale si longitudinale, obtinem legea inductiei
electromagnetice, scrisa pe componente:
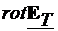 =
= (4.5)
(4.5)
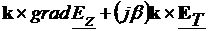 =
=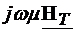 (4.6)
(4.6)
La fel, legea circuitului magnetic, scrisa pe componente, este:
 =
= (4.7)
(4.7)
 =
=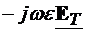 (4.8)
(4.8)
Vom analiza, in
continuare, ghidurile de unda care pe frontiera au pereti perfect conductori,
numite ghiduri cu "pereti electrici". in vecinatatea peretelui perfect
conductor componenta tangentiala a intensitatii campului electric este nula. De
aici, pentru componentele longitudinala si transversala ale intensitatii
campului electric rezulta conditiile pe forntiera W a domeniului W
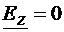 (4.9)
(4.9)
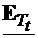 =0 sau
=0 sau  =0 (4.10)
=0 (4.10)
unde t este versorul tangent
la W (Fig.4.1)
inmultim vectorial
relatia (4.6), la stanga, cu versorul k.
|inand cont de formula dublului produs vectorial /1/:  =
=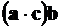
 si de faptul ca
si de faptul ca  ,
,  ,
, 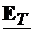 si
si  sunt ortogonale pe
directia k, rezulta:
sunt ortogonale pe
directia k, rezulta:
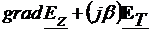 =
=
inlocuind  din relatia (4.8) si
notand
din relatia (4.8) si
notand  =
= , obtinem:
, obtinem:
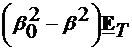 =
=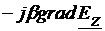 +
+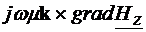 (4.11)
(4.11)
Asemanator, inmultind vectorial relatia (4.8), la stanga, cu versorul k si inlocuind  din (4.6), rezulta:
din (4.6), rezulta:
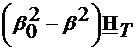 =
=
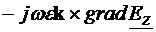 (4.12)
(4.12)
Pentru intensitatea campului electric, conditiile de frontiera sunt
date de relatiile (4.9) si (4.10). inmultim scalar relatia (4.11) cu versorul
tangent t. Din conditiile de
frontiera (4.9) si (4.10), rezulta  =0 si
=0 si 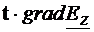 =
=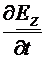 =0 si, deoarece
=0 si, deoarece 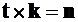 (Fig.4.1), avem:
(Fig.4.1), avem:
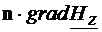 =
=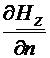 =0 (4.13)
=0 (4.13)
Reciproc, daca 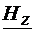 verifica conditia de
frontiera (4.13) si
verifica conditia de
frontiera (4.13) si 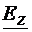 verifica (4.9), atunci
verifica (4.9), atunci
 verifica conditia de
frontiera (4.10).
verifica conditia de
frontiera (4.10).
inmultind scalar relatia
relatia (4.6) cu versorul n si, tinand
cont de relatia 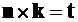 si de conditiile de
frontiera (4.11), (4.12), rezulta:
si de conditiile de
frontiera (4.11), (4.12), rezulta:
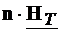 =0 (4.14)
=0 (4.14)
Relatiile (4.13) si (4.14) sunt conditiile de frontiera pentru
componentele intensitatii campului magnetic.
Observatie. Relatiile (4.11) si (4.12) arata ca, pentru 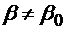 ,
,  si
si  sunt definite de "variabilele" independente
sunt definite de "variabilele" independente  ,
,  . Se observa ca daca
. Se observa ca daca  =0, atunci
=0, atunci 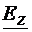 =ct, si, deoarece pe frontiera,
=ct, si, deoarece pe frontiera, 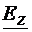 =0 (4.9),
=0 (4.9), 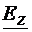 =0 in intreg domeniul W. De asemenea, daca
=0 in intreg domeniul W. De asemenea, daca  =0, atunci
=0, atunci 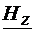 =ct. Folosind relatia lui Stokes si tinand cont de faptul ca
=ct. Folosind relatia lui Stokes si tinand cont de faptul ca  are componenta tangentiala
nula pe frontiera W avem:
are componenta tangentiala
nula pe frontiera W avem: 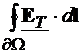 =
=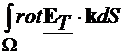 =0. Din relatia (4.5) rezulta ca
=0. Din relatia (4.5) rezulta ca 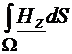 =0, deci
=0, deci 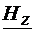 =0.
=0.
Ghiduri
omogene, fara pierderi
in medii omogene,  (Cap.II.5) si
(Cap.II.5) si 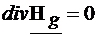 . Scrise pe componente, aceste conditiile de divergenta nula
sunt:
. Scrise pe componente, aceste conditiile de divergenta nula
sunt:
 (4.15)
(4.15)
 (4.16)
(4.16)
in medii omogene, ecuatia
undelor este (2.35'):
 (4.17)
(4.17)
unde

 =
= (4.18)
(4.18)
.Dar tinand cont de forma lui 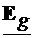 , definit de propagarea de-a lungul ghidului (4.1), avem:
, definit de propagarea de-a lungul ghidului (4.1), avem:
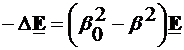 . (4.19)
. (4.19)
Ecuatia (4.19) are pe x, y ca
variabile, iar necunoscuta 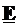 are componente in
planul transversal
are componente in
planul transversal 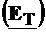 si pe directia
longitudinala
si pe directia
longitudinala 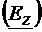 . Scriind ecuatia
(4.19) pe componente, avem:
. Scriind ecuatia
(4.19) pe componente, avem:
 (4.20)
(4.20)
cu conditiile de frontiera (4.10) si:
 . (4.21)
. (4.21)
cu conditiile de frontiera (4.9). Aplicand
operatorul rot relatiei (4.8),
prelucrand dublul produs vectorial si tinand cont de proprietatea  , rezulta:
, rezulta:

Utilizand si relatiile (4.5) si (4.16), rezulta:
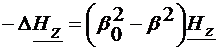 (4.22)
(4.22)
Ecuatia (4.22) este identica cu (4.21), dar are conditiile de frontiera
(4.13). Aplicam operatorul rot relatiei
(4.7), luand in considerare proprietatea 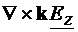 =
= si eliminand aceasta expresie din relatia (4.12), avem:
si eliminand aceasta expresie din relatia (4.12), avem:
 =
=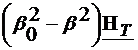 +
+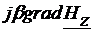
Utilizand proprietatea  =
=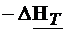 +
+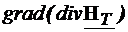 si relatia (4.16), relatia de mai sus devine:
si relatia (4.16), relatia de mai sus devine:
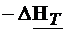 =
=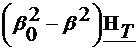 (4.23)
(4.23)
Ecuatia (4.23) este identica cu (4.20), dar are conditiile de frontiera
(4.14).
Teorema 4.1. Presupunem 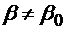 . Daca
. Daca 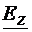 verifica ecuatia
(4.21), cu conditia de frontiera (4.9) si
verifica ecuatia
(4.21), cu conditia de frontiera (4.9) si 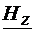 verifica ecuatia
(4.22), cu conditia de frontiera (4.13), atunci
verifica ecuatia
(4.22), cu conditia de frontiera (4.13), atunci 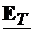 verifica ecuatia
(4.20) cu conditia de frontiera (4.10) si
verifica ecuatia
(4.20) cu conditia de frontiera (4.10) si  verifica ecuatia
(4.23) cu conditia de frontiera (4.14).
verifica ecuatia
(4.23) cu conditia de frontiera (4.14).
Demonstratie. Afirmatia
privind conditiile de frontiera a fost dovedita mai sus.
Aplicam operatorul
(scalar) 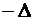 relatiei (4.11) si,
dupa schimbarea ordinei de derivare, acem:
relatiei (4.11) si,
dupa schimbarea ordinei de derivare, acem:
 =
= +
+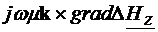
Deoarece 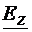 si
si 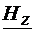 verifica ecuatiile (4.21) si, respectiv, (4.22), rezulta:
verifica ecuatiile (4.21) si, respectiv, (4.22), rezulta:
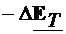 =
=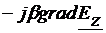 +
+
inlocuind membrul drept din relatia (4.11), rezulta ecuatia (4.20).
Asemanator se arata ca  verifica ecuatia
(4.23). ■
verifica ecuatia
(4.23). ■
in general, pentru o
valoare data a factorului  , este posibil ca ecuatiile (4.21) si (4.22) sa nu fie
verificate simultan de valori nenule ale lui
, este posibil ca ecuatiile (4.21) si (4.22) sa nu fie
verificate simultan de valori nenule ale lui 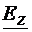 si
si 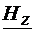 . in acest caz, una
din componentele
. in acest caz, una
din componentele 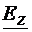 sau
sau 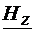 poate fi nula.
poate fi nula.
3.
Modul TEM.
Este interesant de
analizat cazul in care "variabilele"  ,
,  sunt nule, in relatiile (4.11) si (4.12). Conform Observatiei
de la Cap.2,
sunt nule, in relatiile (4.11) si (4.12). Conform Observatiei
de la Cap.2, 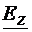 =0 si
=0 si 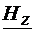 =0. Relatiile (4.11) si (4.12) arata ca singura posibilitate
de a avea componente transversale
=0. Relatiile (4.11) si (4.12) arata ca singura posibilitate
de a avea componente transversale 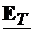 si
si  nenule este oferita
doar de conditia:
nenule este oferita
doar de conditia:
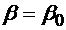 (4.24)
(4.24)
Din interpretarea data lui 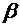 la inceputul Cap.1 si
din relatia (4.18), rezulta
la inceputul Cap.1 si
din relatia (4.18), rezulta 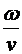 =
= , deci viteza de faza v
este egala cu viteza luminii c,
indiferent de pulsatia
, deci viteza de faza v
este egala cu viteza luminii c,
indiferent de pulsatia
Daca Hz = 0, din (4.5)
rezulta  , cu conditia de frontiera
, cu conditia de frontiera 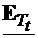 =0 pe W. Potentialul
=0 pe W. Potentialul  poate fi nenul doar daca
W este formata din mai multe
suprafete disjuncte (vezi teorema de unicitate din /1/). Deci trebuie ca ghidul
de unda sa aiba cel putin 2 armaturi (de exemplu cablul coaxial, linia
microstrip). Din (4.15) rezulta ca
poate fi nenul doar daca
W este formata din mai multe
suprafete disjuncte (vezi teorema de unicitate din /1/). Deci trebuie ca ghidul
de unda sa aiba cel putin 2 armaturi (de exemplu cablul coaxial, linia
microstrip). Din (4.15) rezulta ca 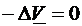 , cu valori V=ct.
pe armaturi. Determinrea potentialului
, cu valori V=ct.
pe armaturi. Determinrea potentialului  este o problema de
electrostatica.
este o problema de
electrostatica.
Deoarece 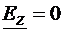 , din relatia (4.6) rezulta:
, din relatia (4.6) rezulta:
 (4.25)
(4.25)
Deoarece atat
intensitatea campului magnetic, cat si intensitatea campului electric au
componentele longitudinale (pe oz)
nule, spunem ca avem modul Transversal Electro Magnetic (TEM) de propagare.
Toate frecventele din modul TEM au aceeasi viteza de faza.
Modul TEM este cel
adoptat la analiza liniilor lungi, omogene, fara pierderi. Acestea sunt tot
ghiduri de unda. De multe ori, modelul este adoptat, cu buna aproximatie si la
linii lungi cu pierderi relativ mici si la ghiduri neomogene. in aceste cazuri,
spunem ca avem mod cvaziTEM.
Concluzie. Modul TEM
poate exista doar in ghiduri de unda cu mai multe armaturi si este definit de
conditia:
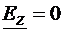 ,
, 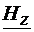 = 0
= 0
echivalenta cu conditia: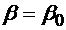 . Componenta transversala a lui E este:
. Componenta transversala a lui E este:
 (4.26)
(4.26)
unde potentialul V
verifica ecuatia:
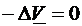 (4.27)
(4.27)
si conditiile de frontiera V=ct.=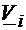 pe armaturile i.
Componenta transversala a lui H
este:
pe armaturile i.
Componenta transversala a lui H
este:
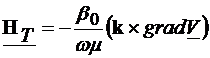
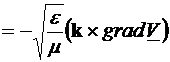 (4.28)
(4.28)
4. Moduri TM
in general, pentru o
valoare data a factorului  , ecuatiile (4.21) si (4.22) nu sunt verificate simultan de
valori nenule ale lui
, ecuatiile (4.21) si (4.22) nu sunt verificate simultan de
valori nenule ale lui 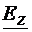 si
si 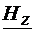 . in acest caz, una
din componentele
. in acest caz, una
din componentele 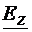 sau
sau 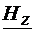 poate fi nula.
poate fi nula.
Sa presupunem ca 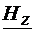 =0. Ramane "variabila"
=0. Ramane "variabila" 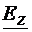 , care verifica ecuatia (4.21). Solutiile nenule
, care verifica ecuatia (4.21). Solutiile nenule  ale ecuatiei (4.21),
numite functii proprii, sunt functii reale si corespund valorilor proprii
reale, pozitive
ale ecuatiei (4.21),
numite functii proprii, sunt functii reale si corespund valorilor proprii
reale, pozitive 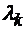 >0, operatorul -, fiind pozitiv definit si
simetric /8/:
>0, operatorul -, fiind pozitiv definit si
simetric /8/:
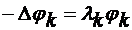 . (4.29)
. (4.29)
Functiile  sunt nule pe frontiera
(4.9). Deci:
sunt nule pe frontiera
(4.9). Deci:
 =
= (4.30)
(4.30)
Spunem ca fiecare valoare proprie 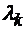 defineste un mod de
propagare
defineste un mod de
propagare  . Le vom spune moduri transversal magnetic (TM), deoarece
intensitatea campului magnetic are doar componenta transversala. Avem
. Le vom spune moduri transversal magnetic (TM), deoarece
intensitatea campului magnetic are doar componenta transversala. Avem  =
=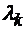 , de unde:
, de unde:
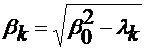 (4.31)
(4.31)
Folosind relatia (4.18), rezulta ca viteza de faza este:
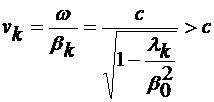
si, pentru 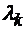 fixat, depinde de
pulsatia . (Unda
electromagnetica se propaga cu viteza c).
Frecventa de taiere pentru propagarea lui
fixat, depinde de
pulsatia . (Unda
electromagnetica se propaga cu viteza c).
Frecventa de taiere pentru propagarea lui  =
= este data de conditia
este data de conditia 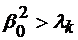 , deci:
, deci:
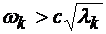
Sub aceasta frecventa de taiere,  capata valori
imaginare (4.31) si, din relatia (4.1), rezulta o unda care se atenueaza.
capata valori
imaginare (4.31) si, din relatia (4.1), rezulta o unda care se atenueaza.
La frecventa data,
sunt valabile doar valorile proprii 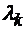 care fac reala
expresia (4.31). Avem deci un numar finit de valori proprii
care fac reala
expresia (4.31). Avem deci un numar finit de valori proprii 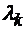 si de moduri
si de moduri  .
.
Deoarece  =
=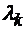 , din relatiile (4.11) si (4.12) rezulta:
, din relatiile (4.11) si (4.12) rezulta:
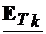 =
=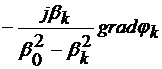 =
= 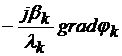 (4.32)
(4.32)
 =
=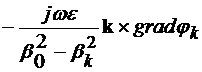 =
= (4.33)
(4.33)
5. Moduri TE
Sa presupunem acum ca 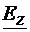 =0. Ramane "variabila"
=0. Ramane "variabila" 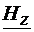 , care verifica ecuatia (4.22). Solutiile nenule
, care verifica ecuatia (4.22). Solutiile nenule  ale ecuatiei (4.22),
numite functii proprii, sunt functii reale si corespund valorilor proprii
reale, pozitive
ale ecuatiei (4.22),
numite functii proprii, sunt functii reale si corespund valorilor proprii
reale, pozitive 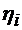 >0:
>0:
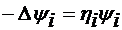 . (4.34)
. (4.34)
Ecuatia de valori si functii proprii (4.33) este identica cu (4.29),
dar spre deosebire de functiile  , care erau nule pe frontiera, functiile
, care erau nule pe frontiera, functiile  au derivata nula pe
directia normalei (4.13). Valorile proprii
au derivata nula pe
directia normalei (4.13). Valorile proprii 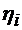 si functiile proprii
si functiile proprii  sunt diferite de
sunt diferite de 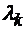 si, respectiv,
si, respectiv,  . Deci:
. Deci:
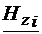 =
= (4.35)
(4.35)
Spunem ca fiecare valoare proprie 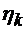 defineste un mod de propagare
defineste un mod de propagare
 , pe care-l vom numi transversal magnetic (TM), deoarece
intensitatea campului electric are doar componenta transversala.
, pe care-l vom numi transversal magnetic (TM), deoarece
intensitatea campului electric are doar componenta transversala.
Deoarece 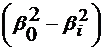 =
=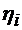 , din relatiile (4.11) si (4.12) rezulta:
, din relatiile (4.11) si (4.12) rezulta:
 =
= =
=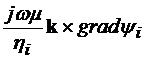 (4.36)
(4.36)
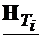 =
= =
= (4.37)
(4.37)
6.
Descompunerea in moduri a undei electromagnetice din ghid
Sa presupunem ca in
ghidul avem unda electromagnetica caracterizata de marimile  . Conform celor prezentate in capitolele precedente, doar
anumite valori ale lui
. Conform celor prezentate in capitolele precedente, doar
anumite valori ale lui 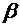 asigura existenta
acestor marimi. Deci, in cazul general,
asigura existenta
acestor marimi. Deci, in cazul general,  poate fi doar o suma
de termeni corespunzatori valorilor lui
poate fi doar o suma
de termeni corespunzatori valorilor lui 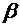 :
:
 =
= +
+
+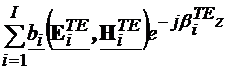 (4.38)
(4.38)
unde:
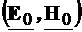 corespunde modului TEM
(
corespunde modului TEM
(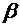 =
=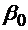 ),
),
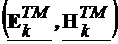 corespunde modului TM,
corespunde modului TM,
 corespunde valorilor
proprii ale modului TM,
corespunde valorilor
proprii ale modului TM,
K este numarul maxim de valori proprii admise de
modul TM, la frecventa de lucru,
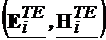 corespunde modului TE,
corespunde modului TE,
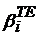 corespunde valorilor
proprii ale modului TE,
corespunde valorilor
proprii ale modului TE,
I este numarul maxim de valori proprii admise de
modul TE, la frecventa de lucru.
Conform rezultatelor
prezentate la Cap.3.4.5, componentele longitudinale si transversale pentru 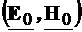 sunt:
sunt:
 =
=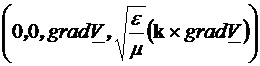 (4.39)
(4.39)
unde potentialul V
verifica ecuatia 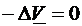 (4.27) si conditiile
de frontiera V=ct.=
(4.27) si conditiile
de frontiera V=ct.=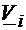 pe armaturile i.
pe armaturile i.
|inand cont de (4.30),
(4.32) si (4.33), componentele longitudinale si transversale pentru 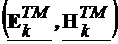 sunt:
sunt:

= (4.40)
(4.40)
unde  verifica ecuatia
verifica ecuatia 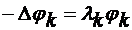 (4.29) si are valori
nule pe frontiera (4.9).
(4.29) si are valori
nule pe frontiera (4.9).
|inand cont de (4.35),
(4.36) si (4.37), componentele longitudinale si transversale pentru 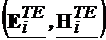 sunt:
sunt:
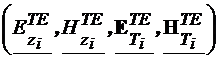
= (4.41)
(4.41)
unde  verifica ecuatia
verifica ecuatia 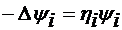 (4.34) si are derivata
nula pe directia normalei (4.13).
(4.34) si are derivata
nula pe directia normalei (4.13).
Daca componentele
longitudinale si transversale pentru  sunt
sunt 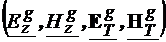 , atunci fiecare componenta se scrie in serie de moduri, ca in
relatia (4.38). Pentru componentele longitudinale ale intensitatii campului
electric si magnetic, avem:
, atunci fiecare componenta se scrie in serie de moduri, ca in
relatia (4.38). Pentru componentele longitudinale ale intensitatii campului
electric si magnetic, avem:
 =
=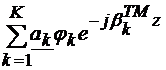 (4.42)
(4.42)
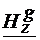 =
= (4.43)
(4.43)
Pentru componentele transversale ale intensitatii campului electric si
magnetic, avem:
 =
=

+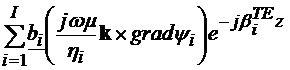 (4.44)
(4.44)
 =
=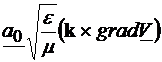

 (4.45)
(4.45)
Conform Anexei C,
coeficientii 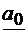 ,
, 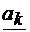 ,
,  se pot obtine inmultind
vectorial relatia (4.44) cu functiile
se pot obtine inmultind
vectorial relatia (4.44) cu functiile  ,
,  si, respectiv,
si, respectiv,  si determinand apoi
fluxul pe W
si determinand apoi
fluxul pe W
7. Puterea electromagnetica
transmisa pe ghid
Puterea complexa
transmisa printr-o sectiune oarecare a ghidului este data de fluxul vectorului
Poynting complex:
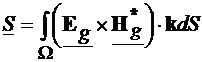 =
=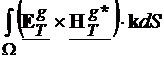
|inand cont de Anexa C, rezulta:
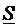 =
= +
+
+ (4.46)
(4.46)
Deci puterea complexa transmisa pe ghid este suma puterilor transmise
pe moduri. |inand cont de proprietatile P1, P4 si P8 din Anexa C, mai putem
scrie:
 =
=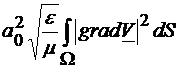 +
+
+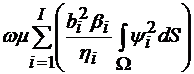 (4.47)
(4.47)
Observatii. 1. Puterea complexa trimisa prin ghidul fara pierderi
are doar componenta reala. Deci ghidul transfera doar putere activa.
2. Puterea transferata
pe modul TEM nu depunde de frcventa si este proportionala cu energia campului
electric rezolvat in problema de electrostatica 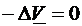 , cu conditiile de frontiera V=ct.=
, cu conditiile de frontiera V=ct.=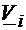 pe armaturile i.
pe armaturile i.
3. De multe ori este convenabil
sa alegem functiile proprii  si
si  de norma unitara, adica
de norma unitara, adica
 =1. in acest caz relatia (4.47) se simplifica:
=1. in acest caz relatia (4.47) se simplifica:
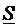 =
=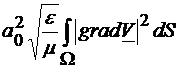 +
+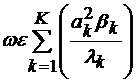 +
+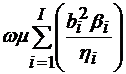 (4.48)
(4.48)
4. Deoarece 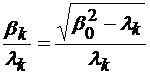 , rezulta ca puterea transmisa pe modurile TM (la fel si pe
TE) este mai mica la moduri superioare.
, rezulta ca puterea transmisa pe modurile TM (la fel si pe
TE) este mai mica la moduri superioare.
5. Valorile si functiile
proprii ale ghidului depind doar de forma geometrica a ghidului. Daca marim
frecventa, atunci, din relatia  , rezulta ca puterea transferata prin ghid este mai mare. Din
pacate, adaptarea ghidului la sarcina ne obliga sa lucram pe o anumita frecventa
si atunci este de preferat ca ghidul sa fie astfel proiectat incat sa fie un
filtru trece-sus. Dimensiunile sale sunt astfel alese incat, la frecventa de
lucru sa obtinem modul cel mai jos (valoarea cea mai mica pentru
, rezulta ca puterea transferata prin ghid este mai mare. Din
pacate, adaptarea ghidului la sarcina ne obliga sa lucram pe o anumita frecventa
si atunci este de preferat ca ghidul sa fie astfel proiectat incat sa fie un
filtru trece-sus. Dimensiunile sale sunt astfel alese incat, la frecventa de
lucru sa obtinem modul cel mai jos (valoarea cea mai mica pentru 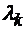 ).
).
8.
Aplicatie. Ghidul dreptunghiular
 Fie ghidul din Fig.4.2., unde a =
62mm, b = 35mm. Pentru a gasi functiile
si valorile proprii in ecuatiile (4.29) si (4.34), folosim metoda separarii variabilelor /9/. Scriem:
Fie ghidul din Fig.4.2., unde a =
62mm, b = 35mm. Pentru a gasi functiile
si valorile proprii in ecuatiile (4.29) si (4.34), folosim metoda separarii variabilelor /9/. Scriem:
 =
=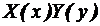
Din ecuatia (4.29), rezulta:
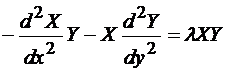 (4.49)
(4.49)
impartind cu  , avem:
, avem:
 (4.50)
(4.50)
Fiecare termen din membrul stang al relatiei (4.50) trebuie sa fie o constanta, daca suma lor este o constanta. Rezulta:
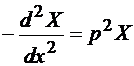 (4.51)
(4.51)
si
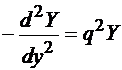 (4.52)
(4.52)
Cele doua ecuatii diferentiale au radacinile:

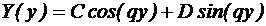
Pentru a gasi modurile
TM, punem conditia ca functia proprie 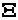 sa fie nula pe
frontiera:
sa fie nula pe
frontiera:
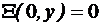 ,
,  ,
, 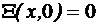 ,
, 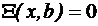 (4.53)
(4.53)
Rezulta:
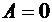 ,
, 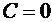 ,
, 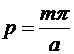 ,
,  ,
, 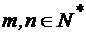 (4.54)
(4.54)
Deci:
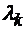 =
=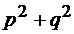 =
= +
+ (4.55)
(4.55)
si:
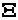 =
= =
= ==
==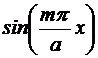
 (4.56)
(4.56)
unde k este indicele de numarare
a perechilor 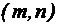 . Se vede usor ca solutiile asociate valorilor
. Se vede usor ca solutiile asociate valorilor 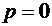 sau
sau  nu sunt convenabile
(de exemplu, conditiile de frontiera nule impuse lui
nu sunt convenabile
(de exemplu, conditiile de frontiera nule impuse lui 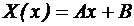 conduc la
conduc la  ).
).
Cea mai mica valoare
proprie este 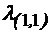 =
= +
+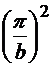 si corespunde modului TM:
si corespunde modului TM: 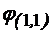 =
=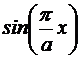
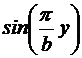 . Frecventa de taiere este deci (Cap.4):
. Frecventa de taiere este deci (Cap.4):
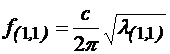 = 4.92GHz (4.57)
= 4.92GHz (4.57)
Pentru a gasi modurile
TE, punem conditia ca, pe frontiera, derivatele functiei proprii 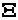 , pe directia normalei sa fie nule:
, pe directia normalei sa fie nule:
 ,
, 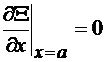 ,
, 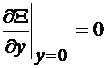 ,
,  (4.58)
(4.58)
in acest caz, sunt valabile si valorile 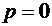 ,
, 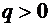 , pentru care se obtine:
, pentru care se obtine:
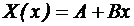 ,
,
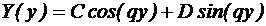
Din conditiile de frontiera rezulta:
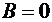 ,
,  si
si  ,
, 
Valorile proprii sunt:
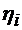 =
=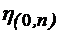 =
= (4.59)
(4.59)
iar modurile TE corespunzatoare sunt:
 =
= =
=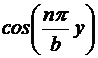 (4.60)
(4.60)
De asemenea sunt
valabile si valorile  ,
, 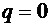 , pentru care se obtine:
, pentru care se obtine:

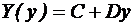
Din conditiile de frontiera rezulta:
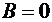 ,
,  si
si 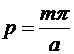 ,
, 
Valorile proprii sunt:
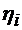 =
=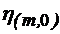 =
= (4.61)
(4.61)
iar modurile TE corespunzatoare sunt:
 =
=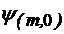 =
= (4.62)
(4.62)
Pentru  ,
,  , rezulta:
, rezulta:
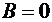 ,
,  ,
, 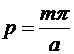 ,
,  ,
, 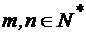
Deci:
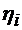 =
=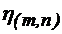 =
=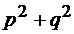 =
= +
+ (4.63)
(4.63)
si:
 =
= =
=
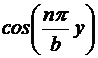 (4.64)
(4.64)
unde i este indicele de numarare
a perechilor 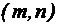 . Cea mai mica valoare proprie este
. Cea mai mica valoare proprie este  =
=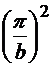 sau
sau  =
= si corespunde modulurilor TE:
si corespunde modulurilor TE:  =
=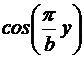 sau, respectiv,
sau, respectiv,  =
=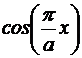 . in cazul numeric ales, cea mai mica valoare proprie
corespunde modului TE(1,0). Frecventa de taiere este:
. in cazul numeric ales, cea mai mica valoare proprie
corespunde modului TE(1,0). Frecventa de taiere este:
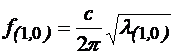 =2.42GHz (4.57)
=2.42GHz (4.57)


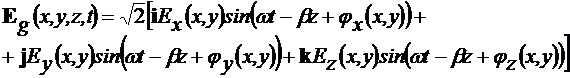
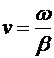 este numita viteza de
faza, marimea
este numita viteza de
faza, marimea 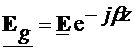 (4.1)
(4.1)
 (4.3)
(4.3)
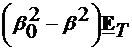 =
=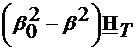 =
=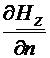 =0 (4.13)
=0 (4.13)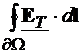 =
=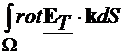 =0. Din relatia (4.5) rezulta ca
=0. Din relatia (4.5) rezulta ca 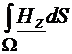 =0, deci
=0, deci 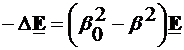 . (4.19)
. (4.19) (4.20)
(4.20) . (4.21)
. (4.21) , rezulta:
, rezulta: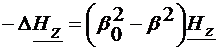
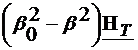 +
+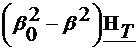
 =
= , este posibil ca ecuatiile (4.21) si (4.22) sa nu fie
verificate simultan de valori nenule ale lui
, este posibil ca ecuatiile (4.21) si (4.22) sa nu fie
verificate simultan de valori nenule ale lui  (4.25)
(4.25)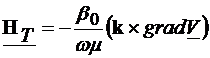
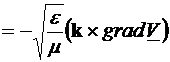
 =
=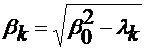 (4.31)
(4.31)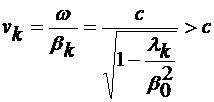
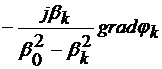 =
= 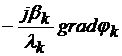 (4.32)
(4.32)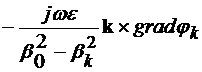 =
=
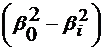 =
=
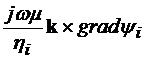 (4.36)
(4.36) =
= (4.37)
(4.37) . Conform celor prezentate in capitolele precedente, doar
anumite valori ale lui
. Conform celor prezentate in capitolele precedente, doar
anumite valori ale lui 
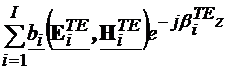 (4.38)
(4.38)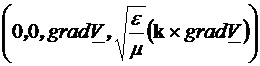 (4.39)
(4.39)
 (4.40)
(4.40)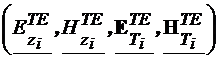
 (4.41)
(4.41)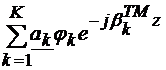


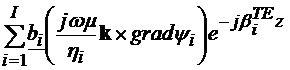
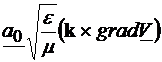

 (4.45)
(4.45)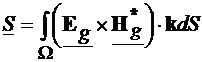 =
=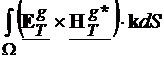
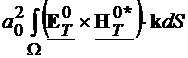 +
+
 (4.46)
(4.46)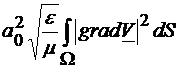 +
+
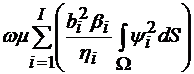 (4.47)
(4.47) =1. in acest caz relatia (4.47) se simplifica:
=1. in acest caz relatia (4.47) se simplifica: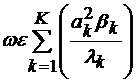 +
+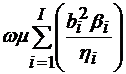 (4.48)
(4.48)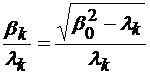 , rezulta ca puterea transmisa pe modurile TM (la fel si pe
TE) este mai mica la moduri superioare.
, rezulta ca puterea transmisa pe modurile TM (la fel si pe
TE) este mai mica la moduri superioare. , rezulta ca puterea transferata prin ghid este mai mare. Din
pacate, adaptarea ghidului la sarcina ne obliga sa lucram pe o anumita frecventa
si atunci este de preferat ca ghidul sa fie astfel proiectat incat sa fie un
filtru trece-sus. Dimensiunile sale sunt astfel alese incat, la frecventa de
lucru sa obtinem modul cel mai jos (valoarea cea mai mica pentru
, rezulta ca puterea transferata prin ghid este mai mare. Din
pacate, adaptarea ghidului la sarcina ne obliga sa lucram pe o anumita frecventa
si atunci este de preferat ca ghidul sa fie astfel proiectat incat sa fie un
filtru trece-sus. Dimensiunile sale sunt astfel alese incat, la frecventa de
lucru sa obtinem modul cel mai jos (valoarea cea mai mica pentru  Fie ghidul din Fig.4.2., unde a =
62mm, b = 35mm. Pentru a gasi functiile
si valorile proprii in ecuatiile (4.29) si (4.34), folosim metoda separarii variabilelor /9/. Scriem:
Fie ghidul din Fig.4.2., unde a =
62mm, b = 35mm. Pentru a gasi functiile
si valorile proprii in ecuatiile (4.29) si (4.34), folosim metoda separarii variabilelor /9/. Scriem:
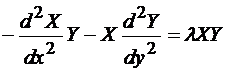 (4.49)
(4.49)
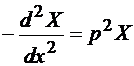
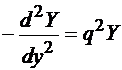
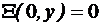 ,
,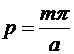 ,
,  ,
,  +
+
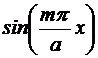

 +
+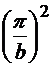 si corespunde modului TM:
si corespunde modului TM: 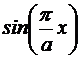
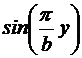 . Frecventa de taiere este deci (Cap.4):
. Frecventa de taiere este deci (Cap.4):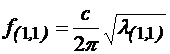 = 4.92GHz (4.57)
= 4.92GHz (4.57) ,
,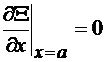 ,
, 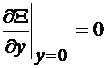 ,
,  (4.58)
(4.58)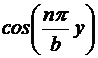


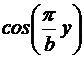 sau, respectiv,
sau, respectiv, 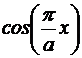 . in cazul numeric ales, cea mai mica valoare proprie
corespunde modului TE(1,0). Frecventa de taiere este:
. in cazul numeric ales, cea mai mica valoare proprie
corespunde modului TE(1,0). Frecventa de taiere este: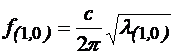 =2.42GHz (4.57)
=2.42GHz (4.57)