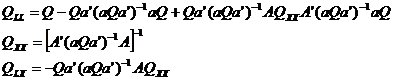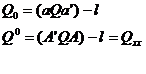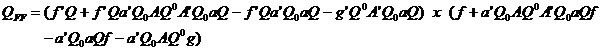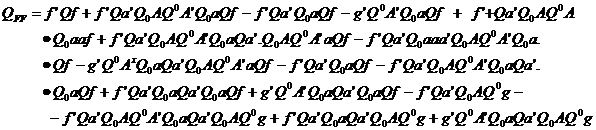Prelucrarea masuratorilor indirecte cu mai multe marimi masurate direct
1 Determinarea
valorilor probabile
Sistemul de ecuatii, corespunzator masuratorilor
indirecte cu mai multe marimi masurate, in scrierea matriciala are
forma:
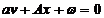
in care:
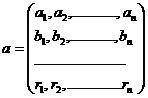
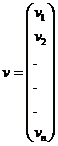

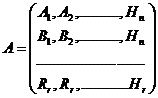
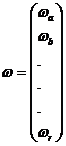

La sistemul se
atasaza conditia:
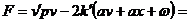 minim (2)
minim (2)
in care:
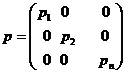
Marimile
masurate direct se considera ca au precizii diferite. Categoria
de masuratori indirecte cu mai multe observatii de aceeasi
precizie nu se va analiza distinct, ci prin particularizarea
masuratorilor de precizii diferite.
In consecinta conditia (2) exista atunci cand:
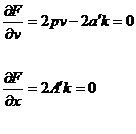
Din egalitatea se obtine:

Cu egalitatea sistemul ecuatiilor normale
are forma:
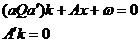
Din sistemul rezulta
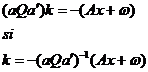
Cu egalitatea
a doua egalitatea din (5) devine:
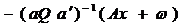 =0
=0
de
unde:
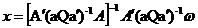 (7)
(7)
Cu valorile marimilor obtinute indirect se determina
valorile coretiilor cu egalitatea
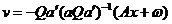 (8)
(8)
2 Calculul preciziilor
2.1 Eroarea medie patratica a
unitatii de pondere se stabileste cu relatia:
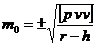
Pentru a obtine valoarea expresiei 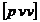 , procedam astfel:
, procedam astfel:
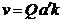
Sau:
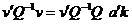
Rezulta:
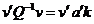
dar:
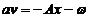
si :
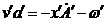
Deci:
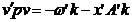
2.2 Expresiile coeficientilor de pondere:
Marimile masurate 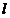 corectate
cu corectiile
corectate
cu corectiile 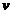 , le
notam cu
, le
notam cu 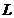 ,
acestea reprezentand, dupa cum se stie, valorile probabile ale
marimilor masurate.
,
acestea reprezentand, dupa cum se stie, valorile probabile ale
marimilor masurate.
Fie, asa dar, in scrierea matriciala,
relatia:
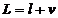
in care:
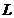 - matricea
coloana a valorilor probabile
- matricea
coloana a valorilor probabile
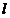 - matricea
coloana a marimilor masurate
- matricea
coloana a marimilor masurate
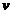 - matricea coloana a corectiilor
probabile
- matricea coloana a corectiilor
probabile
Tinand seama de relatiile si precum si de faptul ca:
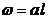
egalitatea
devine:
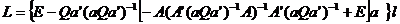
Se poate, de asemenea scrie matricea 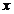 in
functie de elementele masurate
in
functie de elementele masurate 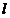 , folosind
relatia:
, folosind
relatia:
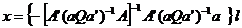
Egalitatiile (13) si pot fi scrise simplificat astfel:
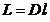
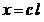 (14')
(14')
Se
intelege ca D si C reprezinta notatiile (matricile) care
raspund expresiilor cuprinse in interiorul acoladelor.
Egalitatiile si (14) pot fi scrise sub forma unei singure
egalitati matriciale si anume:
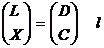
La functia de marimi masurate,
exprimata prin poate fi
aplicata formula (3.34) si avem:


Elementele matricei produs
din (16) se
obtin astfel:
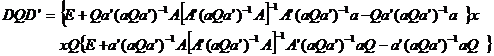
Dupa
inmultiri si reduceri se obtine:
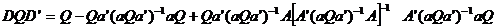 (17)
(17)
Analog se
stabilesc:
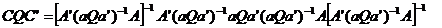
sau:
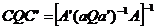 (18)
(18)
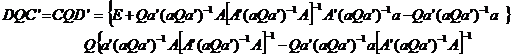 (19)
(19)
Egaland
elementele matricelor din (16) si tinand seama de (17), (18) si
(19) obtinem:
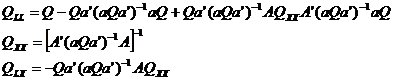 (20)
(20)
2.3
Coeficientul de pondere al unei functii de marimi obtinute prin
masuratori indirecte cu mai multe observatii.
Consideram
functia:
 (21)
(21)
sau
matricial:
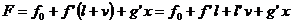 (22)
(22)
in care: 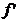 si
si 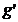 sunt transpusele matricilor coloana ale
coeficientilor din (21).
sunt transpusele matricilor coloana ale
coeficientilor din (21).
Luand in
considerare relatiile (7) si (8) functia de (22) devine:
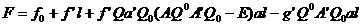
care:
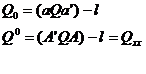
Referindu-ne numai la termenii in 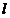 functia (23) se poate scrie:
functia (23) se poate scrie:
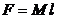
Coeficientul
de pondere al functiei se obtine :
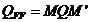
Inlocuind in 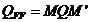 matricea si
atunci avem:
matricea si
atunci avem:
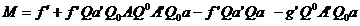
si transpusa:
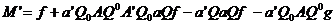
rezulta
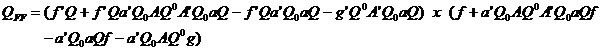
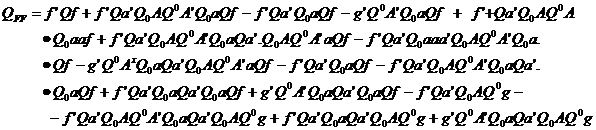
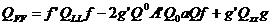


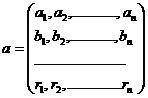
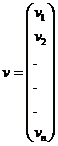

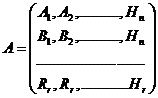
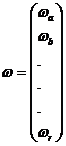
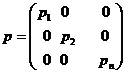
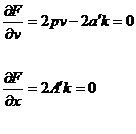
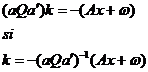

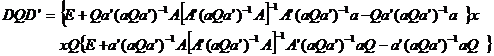
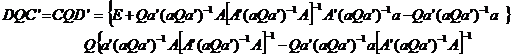 (19)
(19)