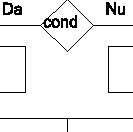Descrierea algoritmilor

DESCRIEREA ALGORITMILOR

1.1 Algoritm, program, programare

Aparitia primelor calculatoare electronice a constituit un salt urias in directia automatizarii activitatii umane. Nu exista astazi domeniu de activitate in care calculatorul sa nu isi arate utilitatea.

Calculatoarele pot fi folosite pentru a rezolva probleme, numai daca pentru rezolvarea acestora se concep programe corespunzatoare de rezolvare. Termenul de program (programare) a suferit schimbari in scurta istorie a informaticii. Prin anii '60 problemele rezolvate cu ajutorul calculatorului erau simple si se gaseau algoritmi nu prea complicati pentru rezolvarea lor. Prin program se intelegea rezultatul scrierii unui algoritm intr‑un limbaj de programare. Din cauza cresterii complexitatii problemelor, astazi pentru rezolvarea unei probleme adesea vom concepe un sistem de mai multe programe.

Dar ce este un algoritm? O definitie matematica, riguroasa, este greu de dat, chiar imposibila fara a introduce si alte notiuni. Vom incerca in continuare o descriere a ceea ce se intelege prin algoritm.

Ne vom familiariza cu aceasta notiune prezentand mai multe exemple de algoritmi si observand ce au ei in comun. Cel mai vechi exemplu este algoritmul lui Euclid, algoritm care determina cel mai mare divizor comun a doua numere naturale. Evident, vom prezenta mai multi algoritmi, cei mai multi fiind legati de probleme accesibile absolventilor de liceu.

Vom constata ca un algoritm este un text finit, o secventa finita de propozitii ale unui limbaj. Din cauza ca este inventat special in acest scop, un astfel de limbaj este numit limbaj de descriere a algoritmilor. Fiecare propozitie a limbajului precizeaza o anumita regula de calcul, asa cum se va observa atunci cand vom prezenta limbajul Pseudocod.

Oprindu-ne la semnificatia algoritmului, la efectul executiei lui, vom observa ca fiecare algoritm defineste o functie matematica. De asemenea, din toate sectiunile urmatoare va reiesi foarte clar ca un algoritm este scris pentru rezolvarea unei probleme. Din mai multe exemple se va observa insa ca, pentru rezolvarea aceleasi probleme, exista mai multi algoritmi.

Pentru fiecare problema P exista date presupuse cunoscute (date initiale pentru algoritmul corespunzator, A) si rezultate care se cer a fi gasite (date finale). Evident, problema s-ar putea sa nu aiba sens pentru orice date initiale. Vom spune ca datele pentru care problema P are sens fac parte din domeniul D al algoritmului A. Rezultatele obtinute fac parte dintr-un domeniu R, astfel ca executand algoritmul A cu datele de intrare xID vom obtine rezultatele rIR. Vom spune ca A(x)=r si astfel algoritmul A defineste o functie

A : D ---> R

Algoritmii au urmatoarele caracteristici: generalitate, finitudine si unicitate.

Prin generalitate se intelege faptul ca un algoritm este aplicabil pentru orice date initiale xID. Deci un algoritm A nu rezolva problema P cu niste date de intrare, ci o rezolva in general, oricare ar fi aceste date. Astfel, algoritmul de rezolvare a unui sistem liniar de n ecuatii cu n necunoscute prin metoda lui Gauss, rezolva orice sistem liniar si nu un singur sistem concret.

Prin finitudine se intelege ca textul algoritmului este finit, compus dintr-un numar finit de propozitii. Mai mult, numarul transformarilor ce trebuie aplicate unei informatii admisibile xID pentru a obtine rezultatul final corespunzator este finit.

Prin unicitate se intelege ca toate transformarile prin care trece informatia initiala pentru a obtine rezultatul rIR sunt bine determinate de regulile algoritmului. Aceasta inseamna ca fiecare pas din executia algoritmului da rezultate bine determinate si precizeaza in mod unic pasul urmator. Altfel spus, ori de cate ori am executa algoritmul, pornind de la aceeasi informatie admisibila xID, transformarile prin care se trece si rezultatele obtinute sunt aceleasi.

In descrierea algoritmilor se folosesc mai multe limbaje de descriere, dintre care cele mai des folosite sunt:

‑ limbajul schemelor logice;

‑ limbajul Pseudocod.

In continuare vom folosi pentru descrierea algoritmilor limbajul Pseudocod care va fi definit in cele ce urmeaza. In ultima vreme schemele logice sunt tot mai putin folosite in descrierea algoritmilor si nu sunt deloc potrivite in cazul problemelor complexe. Prezentam insa si schemele logice, care se mai folosesc in manualele de liceu, intrucat cu ajutorul lor vom preciza in continuare semantica propozitiilor Pseudocod.

1.2 Scheme logice

Schema logica este un mijloc de descriere a algoritmilor prin reprezentare grafica. Regulile de calcul ale algoritmului sunt descrise prin blocuri (figuri geometrice) reprezentand operatiile (pasii) algoritmului, iar ordinea lor de aplicare (succesiunea operatiilor) este indicata prin sageti. Fiecarui tip de operatie ii este consacrata o figura geometrica (un bloc tip) in interiorul careia se va inscrie operatia din pasul respectiv.

Prin executia unui algoritm descris printr-o schema logica se intelege efectuarea tuturor operatiilor precizate prin blocurile schemei logice, in ordinea indicata de sageti.

In descrierea unui algoritm, deci si intr-o schema logica, intervin variabile care marcheaza atat datele cunoscute initial, cat si rezultatele dorite, precum si alte rezultate intermediare necesare in rezolvarea problemei. Intrucat variabila joaca un rol central in programare este bine sa definim acest concept. Variabila defineste o marime care isi poate schimba valoarea in timp. Ea are un nume si, eventual, o valoare. Este posibil ca variabila inca sa nu fi primit valoare, situatie in care vom spune ca ea este neinitializata. Valorile pe care le poate lua variabila apartin unei multimi D pe care o vom numi domeniul variabilei. In concluzie vom intelege prin variabila tripletul

(nume, domeniul D, valoare)

unde valoare apartine multimii D

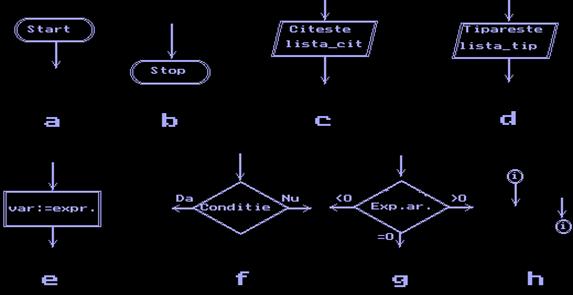
Blocurile delimitatoare Start si Stop (Fig.1.2.1.a si 1.2.1.b) vor marca inceputul respectiv sfarsitul unui algoritm dat printr-o schema logica. Descrierea unui algoritm prin schema logica va incepe cu un singur bloc Start si se va termina cu cel putin un bloc Stop.

Blocurile de intrare/iesire Citeste si Tipareste (Fig. 1.2.1.c si d) indica introducerea unor Date de intrare respectiv extragerea unor Rezultate finale. Ele permit precizarea datelor initiale cunoscute in problema si tiparirea rezultatelor cerute de problema. Blocul Citeste initializeaza variabilele din lista de intrare cu valori corespunzatoare, iar blocul Tipareste va preciza rezultatele obtinute (la executia pe calculator cere afisarea pe ecran a valorilor expresiilor din lista de iesire).

Blocurile de atribuire (calcul) se utilizeaza in descrierea operatiilor de atribuire (:=). Printr-o astfel de operatie, unei variabile var i se atribuie valoarea calculata a unei expresii expr (Fig.1.2.1.e).

Fig.1.2.1. Blocurile schemelor logice

Blocurile de decizie marcheaza punctele de ramificatie ale algoritmului in etapa de decizie. Ramificarea poate fi dubla (blocul logic, Fig.1.2.1.f) sau tripla (blocul aritmetic, Fig. 1.2.1.g). Blocul de decizie logic indica ramura pe care se va continua executia algoritmului in functie de indeplinirea (ramura Da) sau neindeplinirea (ramura Nu) unei conditii. Conditia care se va inscrie in blocul de decizie logic va fi o expresie logica a carei valoare poate fi una dintre valorile 'adevarat' sau 'fals'. Blocul de decizie aritmetic va hotari ramura de continuare a algoritmului in functie de semnul valorii expresiei aritmetice inscrise in acest bloc, care poate fi negativa, nula sau pozitiva.

Blocurile de conectare marcheaza intreruperile sagetilor de legatura dintre blocuri, daca din diverse motive s-au efectuat astfel de intreruperi (Fig.1.2.1.h).

Pentru exemplificare vom da in continuare doua scheme logice, corespunzatoare unor algoritmi pentru rezolvarea problemelor P1.2.1 si P1.2.2.

P1.2.1. Sa se rezolve ecuatia de grad doi aX²+bX+c=0 (a,b,cIR _i a

Metoda de rezolvare a ecuatiei de gradul doi este cunoscuta. Ecuatia poate avea radacini reale, respectiv complexe, situatie recunoscuta dupa semnul discriminantului d = b² - 4ac.

Algoritmul de rezolvare a problemei va citi mai intai datele problemei, marcate prin variabilele a, b si c. Va calcula apoi discriminantul d si va continua in functie de valoarea lui d, asa cum se poate vedea in fig.1.2.2.

Fig.1.2.2. Algoritm pentru rezolvarea ecuatiei de gradul doi.

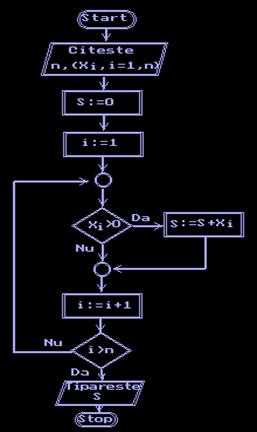
P1.2.2. Sa se calculeze suma elementelor pozitive ale unui sir de numere reale dat.

Schema logica (data in Fig.1.2.3) va contine imediat dupa blocul START un bloc de citire, care precizeaza datele cunoscute in problema, apoi o parte care calculeaza suma ceruta si un bloc de tiparire a sumei gasite, inaintea blocului STOP. Partea care calculeaza suma S ceruta are un bloc pentru initializarea cu 0 a acestei sume, apoi blocuri pentru parcurgerea numerelor: x₁, x_{2 .} x_n si adunarea celor pozitive la suma S. Pentru aceasta parcurgere se foloseste o variabila contor i, care este initializata cu 1 si creste mereu cu 1 pentru a atinge valoarea n, indicele ultimului numar dat.

Fig.1.2.3. Algoritm pentru calculul unei sume.

Schemele logice dau o reprezentare grafica a algoritmilor cu ajutorul unor blocuri de calcul. Executia urmeaza sensul indicat de sageata, putand avea loc reveniri in orice punct din schema logica. Din acest motiv se poate obtine o schema logica incalcita, greu de urmarit. Rezulta importanta compunerii unor scheme logice structurate (D-scheme, dupa Djikstra), care sa contina numai anumite structuri standard de calcul si in care drumurile de la START la STOP sa fie usor de urmarit.

1.3. Limbajul PSEUDOCOD

Limbajul Pseudocod este un limbaj inventat in scopul proiectarii algoritmilor si este format din propozitii asemanatoare propozitiilor limbii romane, care corespund structurilor de calcul folosite in construirea algoritmilor. Acesta va fi limbajul folosit de noi in proiectarea algoritmilor si va fi definit in cele ce urmeaza. Tinand seama ca obtinerea unui algoritm pentru rezolvarea unei probleme nu este intotdeauna o sarcina simpla, ca in acest scop sunt folosite anumite metode pe care le vom descrie in capitolele urmatoare, in etapele intermediare din obtinerea algoritmului vom folosi propozitii curente din limba romana. Acestea sunt considerate elemente nefinisate din algoritm, asupra carora trebuie sa se revina si le vom numi propozitii nestandard. Deci limbajul Pseudocod are doua tipuri de propozitii: propozitii standard, care vor fi prezentate fiecare cu sintaxa si semnificatia (semantica) ei si propozitii nestandard. Asa cum se va arata mai tarziu, propozitiile nestandard sunt texte care descriu parti ale algoritmului inca incomplet elaborate, nefinisate, asupra carora urmeaza sa se revina.

Pe langa aceste propozitii standard si nestandard, in textul algoritmului vom mai introduce propozitii explicative, numite comentarii. Pentru a le distinge de celelalte propozitii, comentariile vor fi inchise intre acolade. Rolul lor va fi explicat putin mai tarziu.

Propozitiile standard ale limbajului Pseudocod folosite in aceasta lucrare, corespund structurilor de calcul prezentate in figura 1.3.1 si vor fi prezentate in continuare. Fiecare propozitie standard incepe cu un cuvant cheie, asa cum se va vedea in cele ce urmeaza. Pentru a deosebi aceste cuvinte de celelalte denumiri, construite de programator, in acest capitol vom scrie cuvintele cheie cu litere mari. Mentionam ca si propozitiile simple se termina cu caracterul ';' in timp ce propozitiile compuse, deci cele in interiorul carora se afla alte propozitii, au un marcaj de sfarsit propriu. De asemenea, mentionam ca propozitiile limbajului Pseudocod vor fi luate in seama in ordinea intalnirii lor in text, asemenea oricarui text al limbii romane.

Prin executia unui algoritm descris in Pseudocod se intelege efectuarea operatiilor precizate de propozitiile algoritmului, in ordinea citirii lor.

In figura 1.3.1, prin A, B s-au notat subscheme logice, adica secvente de oricate structuri construite conform celor trei reguli mentionate in continuare.

Structura secventiala (fig.1.3.1.a) este redata prin concatenarea propozitiilor, simple sau compuse, ale limbajului Pseudocod, care vor fi executate in ordinea intalnirii lor in text. Propozitiile simple din limbajul Pseudocod sunt CITESTE, TIPARESTE, FIE si apelul de subprogram. Propozitiile compuse corespund structurilor alternative si repetitive.

Structura alternativa (fig.1.3.1.b) este redata in Pseudocod prin propozitia DACA, prezentata in sectiunea 1.3.2, iar structura repetitiva din fig.1.3.1.c este redata in Pseudocod prin propozitia CAT TIMP, prezentata in sectiunea 1.3.3.

Bohm si Jacopini [Bohm66] au demonstrat ca orice algoritm poate fi descris folosind numai aceste trei structuri de calcul.

Propozitiile DATE si REZULTATE sunt folosite in faza de specificare a problemelor, adica enuntarea riguroasa a acestora.

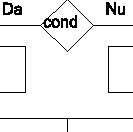
a) structura b) structura c) structura

secventiala alternativa repetitiva Figura 1.3.1. Structurile elementare de calcul

Propozitia DATE se foloseste pentru precizarea datelor initiale, deci a datelor considerate cunoscute in problema (numite si date de intrare) si are sintaxa:

DATE lista ;

unde lista contine toate numele variabilelor a caror valoare initiala este cunoscuta. In general, prin lista se intelege o succesiune de elemente de acelasi fel despartite prin virgula. Deci in propozitia DATE, in dreapta acestui cuvant se vor scrie acele variabile care marcheaza marimile cunoscute in problema.

Pentru precizarea rezultatelor dorite se foloseste propozitia standard

REZULTATE lista ;

in constructia 'lista' ce urmeaza dupa cuvantul REZULTATE fiind trecute numele variabilelor care marcheaza (contin) rezultatele cerute in problema.

Acum putem preciza mai exact ce intelegem prin cunoasterea completa a problemei de rezolvat. Evident, o problema este cunoscuta atunci cand se stie care sunt datele cunoscute in problema si ce rezultate trebuiesc obtinute. Deci pentru cunoasterea unei probleme este necesara precizarea variabilelor care marcheaza date considerate cunoscute in problema, care va fi reflectata printr‑o propozitie DATE si cunoasterea exacta a cerintelor problemei, care se va reflecta prin propozitii REZULTATE. Variabilele prezente in aceste propozitii au anumite semnificatii, presupuse cunoscute. Cunoasterea acestora, scrierea lor explicita, formeaza ceea ce vom numi in continuare specificarea problemei. Specificarea unei probleme este o activitate foarte importanta dar nu si simpla.

De exemplu, pentru rezolvarea ecuatiei de gradul al doilea, specificarea problemei, scrisa de un incepator, poate fi:

DATE a,b,c;   

REZULTATE x1,x2;  

Aceasta specificatie este insa incompleta daca ecuatia nu are radacini reale. In cazul in care radacinile sunt complexe putem nota prin x1, x2 partea reala respectiv partea imaginara a radacinilor. Sau pur si simplu, nu ne intereseaza valoarea radacinilor in acest caz, ci doar faptul ca ecuatia nu are radacini reale. Cu alte cuvinte avem nevoie de un mesaj care sa ne indice aceasta situatie (vezi schema logica 1.2.2), sau de un indicator, fie el ind. Acest indicator va lua valoarea 1 daca radacinile sunt reale si valoarea 0 in caz contrar. Deci specificatia corecta a problemei va fi

DATE a,b,c;

REZULTATE ind,

x1,x2;

Evident ca specificarea problemei este o etapa importanta pentru gasirea unei metode de rezolvare si apoi in proiectarea algoritmului corespunzator. Nu se poate rezolva o problema daca aceasta nu este bine cunoscuta, adica nu avem scrisa specificarea problemei. Cunoaste complet problema este prima regula ce trebuie respectata pentru a obtine cat mai repede un algoritm corect pentru rezolvarea ei.

1.3.1. Algoritmi liniari

Propozitiile CITESTE si TIPARESTE sunt folosite pentru initializarea variabilelor de intrare cu datele cunoscute in problema, respectiv pentru tiparirea (aflarea) rezultatelor obtinute. In etapa de programare propriu-zisa acestor propozitii le corespund intr-un limbaj de programare instructiuni de intrare-iesire.

Propozitia CITESTE se foloseste pentru precizarea datelor initiale, deci a datelor considerate cunoscute in problema (numite si date de intrare) si are sintaxa:

CITESTE lista ;

unde lista contine toate numele variabilelor a caror valoare initiala este cunoscuta.

Deci in propozitia CITESTE, in dreapta acestui cuvant se vor scrie acele variabile care apar in propozitia DATE in specificarea problemei. Se subintelege ca aceste variabile sunt initializate cu valorile cunoscute corespunzatoare.

Pentru aflarea rezultatelor dorite, pe care calculatorul o va face prin tiparirea lor pe hartie sau afisarea pe ecran, se foloseste propozitia standard

TIPARESTE lista ;

in constructia lista ce urmeaza dupa cuvantul TIPARESTE fiind trecute numele variabilelor a caror valori dorim sa le aflam. Ele sunt de obicei rezultatele cerute in problema, specificate si in propozitia REZULTATE.

Blocului de atribuire dintr-o schema logica ii corespunde in Pseudocod propozitia standard

[FIE] var := expresie ;

Aceasta propozitie este folosita pentru a indica un calcul algebric, al expresiei care urmeaza dupa simbolul de atribuire ':=' si de atribuire a rezultatului obtinut variabilei var. Expresia din dreapta semnului de atribuire poate fi orice expresie algebrica simpla, cunoscuta din manualele de matematica din liceu si construita cu cele patru operatii: adunare, scadere, inmultire si impartire (notate prin caracterele +, -, *, respectiv /).

Prin scrierea cuvantului FIE intre paranteze drepte se indica posibilitatea omiterii acestui cuvant din propozitie. El s-a folosit cu gandul ca fiecare propozitie sa inceapa cu un cuvant al limbii romane care sa reprezinte numele propozitiei. De cele mai multe ori vom omite acest cuvant. Atunci cand vom scrie succesiv mai multe propozitii de atribuire vom folosi cuvantul FIE numai in prima propozitie, omitandu-l in celelalte.

Din cele scrise mai sus rezulta ca o variabila poate fi initializata atat prin atribuire (deci daca este variabila din stanga semnului de atribuire :=) cat si prin citire (cand face parte din lista propozitiei CITESTE). O greseala frecventa pe care o fac incepatorii este folosirea variabilelor neinitializate. Evident ca o expresie in care apar variabile care nu au valori nu poate fi calculata, ea nu este definita. Deci nu folositi variabile neinitializate.

Pentru a marca inceputul descrierii unui algoritm vom folosi propozitia:

ALGORITMUL nume ESTE:

fara a avea o alta semnificatie. De asemenea, prin cuvantul SFALGORITM vom marca sfarsitul unui algoritm.

Algoritmii care pot fi descrisi folosind numai propozitiile prezentate mai sus se numesc algoritmi liniari.

Ca exemplu de algoritm liniar prezentam un algoritm ce determina viteza v cu care a mers un autovehicul ce a parcurs distanta D in timpul T.

ALGORITMUL VITEZA ESTE:

CITESTE D,T;

FIE V:=D/T;

TIPARESTE V

SFALGORITM

1.3.2 Algoritmi cu ramificatii

Foarte multi algoritmi executa anumite calcule in functie de satisfacerea unor conditii. Aceste calcule sunt redate de structura alternativa prezentata in figura 1.3.1.b, careia ii corespunde propozitia Pseudocod DACA cond ATUNCI A ALTFEL B SFDACA

sau varianta redusa a ei, DACA cond ATUNCI A SFDACA

folosita in cazul in care grupul de propozitii B este vid.

Aceste propozitii redau in Pseudocod structura alternativa de calcul. Ele cer mai intai verificarea conditiei scrise dupa cuvantul DACA. In caz ca aceasta conditie este adevarata se va executa grupul de propozitii A. In cazul in care aceasta conditie este falsa se va executa grupul de propozitii B, daca este prezenta ramura ALTFEL. Indiferent care dintre secventele A sau B a fost executata, se va continua cu propozitia urmatoare propozitiei DACA.

O generalizare a structurii alternative realizata de propozitia DACA este structura selectiva:

SELECTEAZA i DINTRE

v1: A1;

v2: A2;

. . .

vn: An

SFSELECTEAZA

structura echivalenta cu urmatorul text Pseudocod:

DACA i=v1 ATUNCI A1 ALTFEL

DACA i=v2 ATUNCI A2 ALTFEL

. . .

DACA i=vn ATUNCI An SFDACA

SFDACA

SFDACA

Cu propozitiile prezentate pana aici putem deja descrie destui algoritmi. Acestia se numesc algoritmi cu ramificatii.

Ca exemplu vom scrie un algoritm pentru rezolvarea ecuatiei de gradul al doilea. Am scris mai sus specificatia acestei probleme si am precizat semnificatia variabilelor respective. Pe langa aceste variabile, pentru rezolvarea problemei mai avem nevoie de doua variabile auxiliare:

delta ‑ pentru a retine discriminantul ecuatiei;

r ‑ pentru a retine valoarea radicalului folosit in exprimarea radacinilor.

Ajungem usor la algoritmul dat in continuare.

ALGORITMUL ECGRDOI ESTE:

CITESTE a,b,c;

FIE delta:=b*b‑4*a*c;

DACA delta<0 ATUNCI ind:=0;

r:=radical din (‑delta);

x1:=‑b/(a+a);

x2:=r/(a+a);

ALTFEL ind:=1;

r:=radical din delta;

x1:=(‑b‑r)/(a+a);

x2:=(‑b+r)/(a+a);

SFDACA

TIPARESTE ind, x1,x2;

SFALGORITM

1.3.3 Algoritmi ciclici

In rezolvarea multor probleme trebuie sa efectuam aceleasi calcule de mai multe ori, sau sa repetam calcule asemanatoare. De exemplu, pentru a calcula suma a doua matrice va trebui sa adunam un element al primei matrice cu elementul de pe aceeasi pozitie din a doua matrice, aceasta adunare repetandu‑se pentru fiecare pozitie. Alte calcule trebuiesc repetate in functie de satisfacerea unor conditii. In acest scop in limbajul Pseudocod exista trei propozitii standard: CATTIMP, REPETA si PENTRU.

Propozitia CATTIMP are sintaxa CATTIMP cond EXECUTA A SFCAT

i cere executia repetata a grupului de propozitii A, in functie de conditia 'cond'. Mai exact, se evalueaza conditia 'cond'; daca aceasta este adevarata se executa grupul A si se revine la evaluarea conditiei. Daca ea este falsa executia propozitiei se termina si se continua cu propozitia care urmeaza dupa SFCAT. Daca de prima data conditia este falsa grupul A nu se va executa niciodata, altfel se va repeta executia grupului de propozitii A pana cand conditia va deveni falsa. Din cauza ca inainte de executia grupului A are loc verificarea conditiei, aceasta structura se mai numeste structura repetitiva conditionata anterior. Ea reprezinta structura repetitiva prezentata in figura 1.3.1.c.

Ca exemplu de algoritm in care se foloseste aceasta propozitie dam algoritmul lui Euclid pentru calculul celui mai mare divizor comun a doua numere.

ALGORITMUL Euclid ESTE:

CITESTE n1,n2;

FIE d:=n1; i:=n2;

CATTIMP i 0 EXECUTA

r:=d modulo i; d:=i; i:=r

SFCAT

TIPARESTE d;

SFALGORITM

In descrierea multor algoritmi se intalneste structura repetitiva conditionata posterior:

REPETA A PANA CAND cond SFREP

structura echivalenta cu:    CATTIMP not(cond) EXECUTA A SFCAT

Deci ea cere executia neconditionata a lui A si apoi verificarea conditiei 'cond'. Va avea loc repetarea executiei lui A pana cand conditia devine adevarata. Deoarece conditia se verifica dupa prima executie a grupului A aceasta structura este numita structura repetitiva conditionata posterior, prima executie a blocului A fiind neconditionata.

O alta propozitie care cere executia repetata a unei secvente A este propozitia

PENTRU c:=l_i ;l_f [;p] EXECUTA A SFPENTRU

Ea defineste structura repetitiva predefinita, cu un numar determinat de executii ale grupului de propozitii A si este echivalenta cu secventa

c:=l_i ; final:=l_f ;

REPETA

A

c:=c+p

PANACAND (c>final si p>0) sau (c<final si p<0) SFREP

Se observa ca, in sintaxa propozitiei PENTRU, pasul p este inchis intre paranteze drepte. Prin aceasta indicam faptul ca el este optional, putand sa lipseasca. In cazul in care nu este prezent, valoarea lui implicita este 1.

Semnificatia propozitiei PENTRU este clara. Ea cere repetarea grupului de propozitii A pentru toate valorile contorului c cuprinse intre valorile expresiilor l_i si l_f (calculate o singura data inainte de inceperea ciclului), cu pasul p. Se subintelege ca nu trebuie sa modificam valorile contorului in nici o propozitie din grupul A. De multe ori aceste expresii sunt variabile simple, iar unii programatori modifica in A valorile acestor variabile, incalcand semnificatia propozitiei PENTRU. Deci, nu recalcula limitele si nu modifica variabila de ciclare (contorul) in interiorul unei structuri repetitive PENTRU).

Sa observam, de asemenea, ca prima executie a grupului A este obligatorie, abia dupa modificarea contorului verificandu-se conditia de continuare a executiei lui A.

Ca exemplu, sa descriem un algoritm care gaseste minimul si maximul componentelor unui vector de numere reale. Vom nota prin X acest vector, deci

X = (x₁, x₂, , x_n)

Specificatia problemei este urmatoarea:

DATE n,(x_i ,i=1,n);

REZULTATE valmin,valmax;

iar semnificatia acestor variabile se intelege din cele scrise mai sus. Pentru rezolvarea problemei vom examina pe rand cele n componente. Pentru a parcurge cele n componente avem nevoie de un contor care sa precizeze pozitia la care am ajuns. Fie i acest contor. Usor se ajunge la urmatorul algoritm:

ALGORITMUL MAXMIN ESTE:  

CITESTE n,(x_i,i=1,n);

FIE valmin:=x₁; valmax:=x₁;

PENTRU i:=2,n EXECUTA

DACA x_i<valmin ATUNCI valmin:=x_i SFDACA

DACA x_i>valmax ATUNCI valmax:=x_i SFDACA

SFPENTRU

TIPARESTE valmin,valmax;

SFALGORITM

Un rol important in claritatea textului unui algoritm il au denumirile alese pentru variabile. Ele trebuie sa reflecte semnificatia variabilelor respective. Deci alege denumiri sugestive pentru variabile, care sa reflecte semnificatia lor.

In exemplul de mai sus denumirile valmin si valmax spun cititorului ce s-a notat prin aceste variabile.

1.4 Calculul efectuat de un algoritm

Fie X₁, X₂, , X_n, variabilele ce apar in algoritmul A. In orice moment al executiei algoritmului, fiecare variabila are o anumita valoare, sau este inca neinitializata.

Vom numi stare a algoritmului A cu variabilele mentionate vectorul

s = ( s₁,s₂,,s_n )

format din valorile curente ale celor n variabile ale algoritmului.

Este posibil ca variabila X_j sa fie inca neinitializata, deci sa nu aiba valoare curenta, caz in care s_j este nedefinita, lucru notat in continuare prin semnul intrebarii '?'.

Prin executarea unei anumite instructiuni unele variabile isi schimba valoarea, deci algoritmul isi schimba starea.

Se numeste calcul efectuat de algoritmul A o secventa de stari

s₀, s₁, s₂, , s_m

unde s₀ este starea initiala cu toate variabilele neinitializate, iar s_m este starea in care se ajunge dupa executia ultimei propozitii din algoritm.

1.5 Rafinare in pasi succesivi

Adeseori algoritmul de rezolvare a unei probleme este rezultatul unui proces complex, in care se iau mai multe decizii si se precizeaza tot ceea ce initial era neclar. Observatia este adevarata mai ales in cazul problemelor complicate, dar si pentru probleme mai simple in procesul de invatamant. Este vorba de un proces de detaliere pas cu pas a specificatiei problemei, proces denumit si proiectare descendenta, sau rafinare in pasi succesivi. Algoritmul apare in mai multe versiuni succesive, fiecare versiune fiind o detaliere a versiunii precedente. In versiunile initiale apar propozitii nestandard, clare pentru cititor, dar neprecizate prin propozitii standard. Urmeaza ca in versiunile urmatoare sa se revina asupra lor. Algoritmul apare astfel in versiuni succesive, tot mai complet de la o versiune la alta.

Apare aici o alta regula importanta in proiectarea algoritmului: amana pe mai tarziu detaliile nesemnificative; concentreaza-ti atentia la deciziile importante ale momentului.