MATRICI, VECTORI SI SCALARI
NOTATII
MATLAB este un pachet de programe care
lucreaza numai cu un singur tip de entitati, matrici
rectangulare, cu elemente reale sau complexe.In acest sens, scalarii sunt
asimilati matricilor cu o linie si o coloana (1x1), iar vectorii sunt asimilati
matricilor cu o linie si n coloane (1x n) sau o coloana
si n linii (nx1). Operatiile si comenzile
in MATLAB sunt aproape naturale, in sens matricial, asemanator
modului de calcul obisnuit. Astfel, entitatile :
A=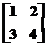 ; B=
; B=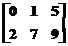 ; C=
; C=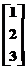 ; D=
; D=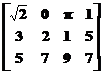 ; E=[1 3 5 7]
; E=[1 3 5 7]
sunt toate matrici in acceptiunea MATLAB: A este o matrice 2x2, B are dimensiunea 2x3, C este 3x1, D este o matrice 3x4 si E este un vector linie 1x4.
Elementele unei matrici, pot fi identificate prin una dintre
notatiile: Aij, A[i,j],
A(i,j) etc. si semnifica elementul de la intersectia liniei
"i" cu coloana "j". Ultima notatie, A(i,j),
este cea care a fost adoptata si in MATLAB si va fi
folosita in continuare. Dimensiunea unei matrici este precizata de o
pereche de numere, care arata numarul de linii si coloane ale
matricei respective: D este o
matrice 3x4; iar o matrice cu o
singura linie sau o singura coloana se numeste vector linie
(matricea E din exemplul anterior)
sau vector coloana (matricea C din
exemplul anterior), elementele acestora putand fi identificate cu un singur
indice. O matrice cu o singura linie si o singura coloana
este un scalar.
Pentru a face referire
la un element A(i,j), (adica
elementul aflat la intersectia liniei i
cu coloana j ) al unei matrici A, sunt necesari doi indici, indicele
de linie si indicele de coloana, in aceasta ordine. Referirea la
un element al unui vector poate fi facuta numai cu un singur indice.
Astfel, daca se introduce de la
tastatura, la promptul MATLAB, (promptul are simbolul grafic " » ") matricile A, B, C, D si E:
»A=[1,2;3,4];B=[0,1,5;2,7,9];C=[1,2,3];D=[sqrt(2),0,pi,1;3,2,1, .
5;5,7,9,7];E=[1,3,5,7]
De exemplu, elementul de pe pozitia (2,1), al matricei A, poate fi apelat cu comanda:
»A(2,1) [Enter]
ans
=
Daca se repeta exemplul, pentru matricile B, D, E:
»B(1,3) [Enter]
ans
=
»D(3,4) [Enter]
ans
=
»E(4) [Enter]
ans
=
7
DEFINIREA
MATRICILOR SIMPLE
Definirea matricilor se face prin una dintre urmatoarele metode:
introducerea explicita a listei de elementelor;
generarea prin instructiuni si
functii;
crearea fisierelor" .m";
incarcare din fisiere de date
externe.
MATLAB nu contine instructiuni de
dimensionare si declaratii de tip, iar memoria este alocata
automat, pana la valoarea maxim disponibila.
Definirea matricilor simple prin
introducerea listei de elemente
Cea mai simpla metoda de definire a
matricilor mici consta in utilizarea unei liste explicite, a elementelor
acesteia, respectand conventiile de scriere. La introducerea unei astfel
de liste trebuie respectate urmatoarele reguli:
a)
elementele matricei sunt cuprinse intre
paranteze drepte " [ ] "
b)
elementele unei linii trebuie separate prin
spatii libere (blanc-uri ) sau virgule;
c)
liniile se separa prin semnul
punct-virgula " ; " ;
Astfel, matricea A=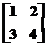 , se introduce de la tastatura cu secventa:
, se introduce de la tastatura cu secventa:
»A=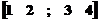 [Enter]
[Enter]
A=
1 2
3 4
Obs. -In acest exemplu:
elementele
unei linii sunt separate printr-un spatiu liber ((blank): 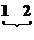 respectiv
respectiv 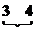 ;
;
[Enter]- reprezinta tasta cu
acelasi nume;
Acelasi rezultat se obtine daca elementele liniei se
separa prin virgula:
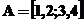
A=
1 2
3 4
Matricea A,
astfel definita, poate fi utilizata in calcule sau poate fi
salvata intr-un fisier de date pentru o folosire ulterioara
(tipul fisierelor de date este .mat).
Pentru matricile mari, la care datele de
intrare nu incap pe o singura linie, se poate proceda la inlocuirea
semnului " ; " cu o apasare a tastei "[Enter]", ca in exemplul urmator:
A=[1,2[Enter]
3,4[Enter]
5,6] [Enter]
si se afiseaza:
A =
1 2
3 4
5 6
Un alt mod de definire
a unei matrici consta in apelarea numelui unui fisier de date aflat
in memoria sistemului de calcul. Acest fisier trebuie sa fi fost
salvat, in prealabil, pe hard-disc, in format ASCII (text), organizat ca o
matrice rectangulara (completa) si trebuie sa aiba
extensia " .m ". Astfel, de exemplu,
daca pe hard-disc se gaseste un fisier cu numele matricea_A.m care contine
urmatoarele linii de text:
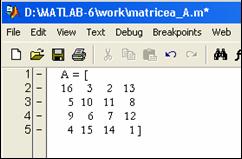
instructiunea care citeste fisierul (si
genereaza matricea "A") este:
» matricea_A
ceea ce va avea ca rezultat afisarea matricei A:
A =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
Afisarea matricei
continuta in fisierul matricea_A.mat, este posibila, la
tastarea numelui acestui fisier, numai in cazul in care acest fisier
este salvat in directorul curent.
Posibilitatea de a importa date din alte
programe va fi abordata in sectiuni ulterioare.
generarea matricilor prin
instructiuni si functii
In MATLAB se pot defini matricile folosind instructiuni si
functii specifice, existand, deasemenea, predefinite matrici implicite.
Generarea matricilor prin instructiuni si functii
utilizeaza facilitatile acestui mediu de programare.
De exemplu, matricile  si
si 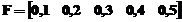 se genereaza
astfel:
se genereaza
astfel:
» E=1:4 [Enter]
E =
1 2 3 4
iar cu secventa urmatoare se obtine matricea F:
» F=0.1:0.1:0.5 [Enter]
F =
0.1000 0.2000 0.3000 0.4000 0.5000
Matricile predefinite,
prin functii MATLAB, sunt:
A). Matricea unitate eye(n), eye(n,m)
Prin secvanta
urmatoare se genereaza matricile unitate avand elementele diagonalei
principale 1 (Atentie! Pentru
afisarea matricilor I2, I3 respectiv I34, este necesara introducerea
numelui acesteia, la prompterul MATLAB, intrucat definirea acestora se incheie
cu caracterul ";" care blocheaza afisarea!):
»
I2=eye(2);I3=eye(3);I34=eye(3,4); [Enter]
I2 =
1 0
0 1
I3
=
1 0 0
0 1 0
0 0 1
I34
=
1 0 0 0
0 1 0 0
0 0 1 0
B). Matricea identica : ones(n),
ones(m,n)
Matricea identica are toate elementele
egale cu cifra 1:
» Y2= ones(2); Y34= ones(3,4);
se obtin rezultatele (dupa ce se introduce, de la
tastatura, numele matricei):
Y2 =
1 1
1 1
Y34
=
1 1 1 1
1 1 1 1
1 1 1 1
C). Matricea zero : zeros(n), zeros(n,m)
Matricea zero are toate elementele egale cu 0 (nu este matricea nula):
»Z3=zeros(3)
Z3 =
0 0 0
0 0 0
0 0 0
D). Matricea vida: [ ]
E).
Matricea "vida" este o
matrice cu, cel putin, una dintre dimensiuni egala cu zero, deci
fara elemente definite, dar matricea exista ca structura
matematica:
»A=[]
F). Matricea aleatoare:
rand(n), rand(n,m), rand(n,m,p)
Functia rand() genereaza matrici ale caror elemente sunt numere
uniform distribuite in intervalul de valori (0,1) . Cu secventa urmatoare se genereaza matricile
arbitrare B3 (cu dimensiunea 3x3), B34(cu dimensiunea 3x4) si B345(cu dimensiunea 3x4 in 5 variante, disponibila numai in versiunile
MATLAB superioare versiunii 5.3 ):
»B3=rand(3);B34=rand(3,4);B345=rand(3,4,5);
fiind obtinute rezultatele:
B3
=
0.4514 0.3127 0.6831
0.0439 0.0129 0.0928
0.0272 0.3840 0.0353
B34 =
0.6124 0.0164 0.0576 0.7176
0.6085 0.1901 0.3676 0.6927
0.0158 0.5869 0.6315 0.0841
B345(:,:,1) =
0.4544 0.1536 0.7275 0.1210
0.4418 0.6756 0.4784 0.4508
0.3533 0.6992 0.5548 0.7159
B345(:,:,2) =
0.8928 0.8656 0.9084 0.0498
0.2731 0.2324 0.2319 0.0784
0.2548 0.8049 0.2393 0.6408
B345(:,:,3)
=
0.1909 0.1708 0.3400 0.3932
0.8439 0.9943 0.3142 0.5915
0.1739 0.4398 0.3651 0.1197
B345(:,:,4) =
0.0381 0.9342 0.8729 0.9669
0.4586 0.2644 0.2379 0.6649
0.8699 0.1603 0.6458 0.8704
B345(:,:,5) =
0.0099 0.4302 0.6873 0.1556
0.1370 0.8903 0.3461 0.1911
0.8188 0.7349 0.1660 0.4225
G). Matricea dispersiilor:sparse (A), sparse(i,j,s,m,n)
Functia sparse() genereaza o matrice
dispersata in raport cu argumentul. Astfel, daca se da matricea 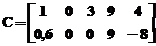 , atunci functia sparse
(C), genereaza matricea:
, atunci functia sparse
(C), genereaza matricea:
»C=[1,0,3,9,4;0.6,0,0,9,8];
» sparse (C)
ans =
(1,1) 1.0000
(2,1) 0.6000
(1,3) 3.0000
(1,4) 9.0000
(2,4) 9.0000
(1,5) 4.0000
(2,5) -8.0000
adica, sunt retinute doar elementele diferite de valoarea zero din matricea C de la argumentul functiei sparse. Aceasta functie este
utila pentru stocarea in memoria calculatorului a matricilor cu m linii si n coloane, unde m si
n sunt valori mari.
H). Matricea Hadamard
Aceasta matrice se genereaza cu
functia sinonima hadamard(n)
cu conditia ca n, n/12 si n/20 sa fie puteri ale lui 2. Matricea Hadamard are
elementele 1 si -1 iar coloanele sunt ortogonale. Utilitatea acestei
matrici se regaseste in combinatorica, procesarea semnalelor
si analiza numerica. Cu secventa urmatoare se obtin
matricea Hadamard de ordinul 4:
»H4=hadamard(4)
H4 =
1 1 1 1
1 -1 1 -1
1 1 -1 -1
1 -1 -1 1
I). Matricea Hilbert
Matricea Hilbert
este un exemplu notabil de matrice slab conditionata. Elementele
matricei Hilbert sunt de forma H(i, j) = 1/(i+j-1), si se
genereaza cu functia MATLAB hilb(n).
De exemplu:
»H3=hilb(3)
H3 =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
J). Matricea magica patratica
Matricea magica
patratica este generata cu functia MATLAB magic(n) si este construita
din intregii cuprinsi intre 1
si n2 cu
conditia ca suma elementelor de pe orice rand sa fie egala cu
suma elementelor de pe oricare coloana respectiv cu suma elementelor de pe
diagonala principala, iar n trebuie
sa fie un scalar mai mare sau egal cu 3:
»M3=magic(3) [Enter]
M3 =
8 1 6
3 5 7
4 9 2
Pentru verificarea conditiei de
egalitate intre suma elementelor pe linie cu suma elementelor pe coloana, respectiv
cu suma elementelor pe diagonala, se realizeaza suma corespunzatoare, folosind o functie Matlab (sum()
)
»
suma_elementelor_pe_linie=sum(M3) [Enter]
suma_elementelor_pe_linie
=
15 15 15
»
suma_elementelor_pe_coloana= sum(M3')
[Enter]
suma_elementelor_pe_coloana
=
15 15 15
»
suma_elementelor_pe_diagonala= sum(diag(M3))
[Enter]
suma_elementelor_pe_diagonala
=
15
»M4=magic(4)
M4 =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
»
suma_elementelor_pe_linie= sum(M4)
suma_elementelor_pe_linie
=
34 34 34 34
»
suma_elementelor_pe_coloana =sum(M4')
suma_elementelor_pe_coloana
=
34 34 34 34
»
suma_elementelor_pe_diagonala= sum(diag(M4))
suma_elementelor_pe_diagonala
=
34
Pentru
afisarea matricilor M3 respectiv M4, se tasteaza numele acesteia.
K). Matricea Pascal
Matricea Pascal
se genereaza cu functia MATLAB, specifica, pascal(n), este o matrice de ordinul n, pozitiv definita, simetrica, cu elemntele, numere intregi,
preluate din Triunghiul lui Pascal (format din coeficientii binomiali),
iar inversa acestei matrici este o matrice cu elementele numere intregi:
»P2=pascal(2);P3=pascal(3);P4=pascal(4);P5=pascal(5);
P2 =
1 1
1 2
P3 =
1 1 1
1 2 3
1 3 6
P4
=
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
P5
=
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
L). Matricea Wilkinson
Cu functia MATLAB wilkinson(n) se genereaza matricea sinonima, care este o
matrice patratica de ordinul n
cu valori proprii, de test, simetrica, tridiagonala, cu perechi
de valori intregi apropiate dar nu exact egale. Cea mai utilizata este
matricea Wilkinson de ordinul 21.
Pentru a se observa cum se construieste matricea Wilkinson se prezinta, mai jos, matricele
corespunzatoare, de ordinul 2, 3, 4, 5, 6:
»doi=wilkinson(2)
doi
=
0.5000 1.0000
1.0000 0.5000
»trei=wilkinson(3)
trei
=
1 1 0
1 0 1
0 1 1
»patru=wilkinson(4)
patru
=
1.5 1 0 0
1 0.5 1 0
0 1 0.5 1
0 0 1 1.5
»cinci=wilkinson(5)
cinci
=
2 1 0 0 0
1 1 1 0 0
0 1 0 1 0
0 0 1 1 1
0 0 0 1 2
»sase=wilkinson(6)
sase
=
2.5 1 0 0 0 0
1 1.5 1 0 0
0
0 1 0.5 1 0 0
0 0 1 0.5 1 0
0 0 0 1 1.5 1
0 0 0 0 1 2.5
Generarea matricilor prin
Crearea fiSierelor SCRIPT
O facilitate oferita de MATLAB, pentru
generarea matricilor, este crearea fisierelor script. De exemplu, pentru
matricea "A", data sub forma algebrica, 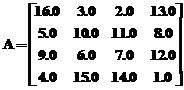 ,
,
se realizeaza fisierul matricea_A.m
astfel:
Din meniul File → New → M-file se creaza fisierul matricea_A care va contine textul
A = [
16.0 3.0 2.0 13.0
5.0 10.0 11.0 8.0
9.0 6.0 7.0 12.0
4.0 15.0 14.0 1.0 ]
Acest fisier se salveaza (din
meniul File →Save As . ) cu numele matricea_A, acestuia fiindu-i
atribuita, implicit, extensia ".m"
Daca
se doreste apelarea fisierului (pentru a fi utilizat in alte
fisiere, sau in Workspace), in
linia de comanda MATLAB, se tasteaza numele fisierului, matricea_A, rezultatul fiind
afisarea matricei A:
»matricea_A
»A =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
Generarea matricilor prin
incarcarea din fisiere externe
O alta
posibilitate de a accesa date din fisiere in format text sau binar, in
MATLAB-6, este aceea de a folosi calea File→ Import Data . care utilizeaza un Import
Wizard (Asistent pentru import date),
acesta solicitand utilizatorului date suplimentare privind calea
fisierului ce urmeaza a fi importat. De exemplu, pentru a importa
fisierul "matrice", care se gaseste pe
hard-disc, in partitia D:/ a
acestuia, D:/MATLAB-6/work/matrice,
se va deschide fereastra de dialog din figura:
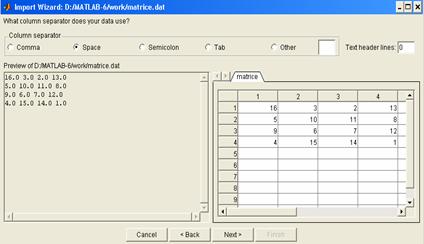
Accesand butonul Next, iar, dupa validarea
operatiei, Finish, in
spatiul de lucru, poate fi, oricand, afisata si
utilizata matricea salvata in acest fisier. Comanda load citeste fisierele binare
continand matrici generate in sesiuni de lucru anterioare. Aceeasi
comanda citeste fisiere- text continand date numerice.
Fisierul text trebuie sa fie organizat ca tabel bi-dimensional (linii
si coloane), separate prin spatii libere (blancuri), cu un rand pe
fiecare linie si numar egal de elemente in fiecare rand (tabelul
trebuie sa aiba acelasi numar de coloane pe fiecare linie). De
exemplu, daca, intr-un editor de text (acest editor poate fi extern MATLAB-ului),
se creeaza fisierul text continand urmatoarele patru linii
de text:
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
si se salveaza fisierul cu numele, matrice, de exemplu, atunci, acest fisier poate fi apelat
folosind urmatoarea succesiune de operatiuni, in Workspace (acest fisier poate fi apelat si de alte
fisiere sau functii MATLAB). De exemplu, presupunand ca in
calcule este necesar ca datele cuprinse in fisierul matrice.dat, stocat in memoria calculatorului, si aceste date
sa fie identificate cu numele "B",
atunci se procedeaza astfel:
»load matrice.dat
»B=matrice
B =
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
ELEMENTELE MATRICILOR
Elementele matricilor
pot fi numere reale sau complexe, sau orice alta expresie MATLAB. De
exemplu, pentru introducerea matricei 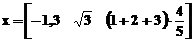 se foloseste
scrierea:
se foloseste
scrierea:
» x=[ -1.3, sqrt(3), (1+2+3)*4/5] [Enter]
rezulta:
»
x=
-1.3000 1.7321 4.8000
Obs. De remarcat faptul ca pentru numarul
rational "-1,3" s-a folosit
formatul britanic: s-a folosit caracterul "."
pentru separarea partii intregi de partea fractionara a
numarului. De asemenea, "sqrt(3) pentru
numarul "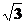 ", elementul x(3) fiind afisat cu valoarea
calculata pentru expresia de mai sus,iar pentru separarea elementelor unei
linii s-a folosit caracterul virgula (,).
", elementul x(3) fiind afisat cu valoarea
calculata pentru expresia de mai sus,iar pentru separarea elementelor unei
linii s-a folosit caracterul virgula (,).
Elementele unei matrici pot fi referite (se
pot apela, sau se poate edita) cu indici cuprinsi intre paranteze rotunde
" ( ) ", cifrele reprezentand
identificatorii de linie, respectiv de coloana ai elementului apelat.
De exemplu, cu instructiunea
urmatoare, se cere afisarea elementului "al doilea" al vectorului x:
» a = x(2) [Enter]
a =
1.7321
in timp ce, cu instructiunea urmatoare se modifica
elementul al cinci-lea al aceluiasi vector x (daca acest element nu exista in varianta originala a
vectorului x, atunci, MATLAB
atribuie automat valoarea inscrisa in partea dreapta a semnului "=", de atribuire):
» x(5) = abs(x(1) ) [Enter]
x=
-1.3000 1.7321 4.8000 0 1.3000
(adica, elementul al 5-lea al vectorului x este egal cu valoarea absoluta a elementului de pe
pozitia 1 a vectorului x), ceea ce returneaza
rezultatul:
Obs:De
remarcat ca se atribuie o valoare unui element care ocupa o
pozitie in afara dimensiunii maxime a matricei sau vectorului referit, iar
elementele nedefinite sunt setate la valoarea zero
Deci, ca regula, se poate deduce
ca in cazul in care pe o
anumita pozitie, intr-o matrice, nu exista un element si se
defineste, folosind o regula oarecare, un element de pe o
pozitie "urmatoare", elementul care lipseste se inlocuieste
automat de catre MATLAB, cu valoarea 0
(zero).In acest sens,
instructiunea urmatoare "adauga" un element pe pozitia
(2,4), si "completeaza" cu zerouri acolo unde nu sunt definite alte
valori, pentru matricea A:
» A=[1,2;3,4];A(2,4) = 6 [Enter]
A=
1 2 0 0
3 4 0 6
(adica elementul din linia 2 coloana 4, al matricei A=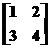 este definit,
de-acum inainte, ca fiind numarul intreg 6,(Atentie! Nu trebuie
inlocuite elementele care lipsesc: A13 , A14, A23,
acest lucru este realizat automat de catre mediul MATLAB )).
este definit,
de-acum inainte, ca fiind numarul intreg 6,(Atentie! Nu trebuie
inlocuite elementele care lipsesc: A13 , A14, A23,
acest lucru este realizat automat de catre mediul MATLAB )).
O modalitate de a
construi matrici mari consta in folosirea matricilor mici ca elemente,
si concatenarea ("legarea") acestora. Spre exemplu, din doua
matrici 2x3 se poate construi o matrice 4x3; dimensiunile matricilor utilizate
trebuind sa fie astfel alese incat sa se realizeze tablouri
rectangulare complete.
Fie A1 si A2 cele doua matrici utilizate. Cu secventa
urmatoare:
» A1=[ 1 2 ; 3 4]; A2=[5 6 ; 7 8]; A =[ A1 ; A2] [Enter]
se obtine rezultatul:
»A=
1 2
3 4
5 6
7 8
O matrice cu dimensiuni reduse poate fi
extrasa din matrici mai mari utilizand semnul " : " (doua puncte). De exemplu:
»B=A(2,3,
:) [Enter]
extrage liniile doi si trei ("2:3")
si toate coloanele din matricea curenta A, obtinandu-se matricea B:
B=
3 4
5 6
In acest exemplu, caracterul "doua
puncte" ( " : " ), folosit in
instructiunea »B=A(2:3, :), are
urmatoarea semnificatie:"se
extrag elementele aflate la intersectia liniilor 2,
3 cu toate coloanele matricei A".
concatenarea matricilor
Concatenarea ("legarea")
este procesul de asamblare a matricilor mici, pentru generarea matricilor
supra- dimensionate (o matrice, in fapt, este
constituita prin concatenarea elementelor proprii). Operatorul de
concatenare este perechea de paranteze drepte, [ ]. De exemplu, fiind data matricea 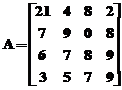 , se poate genera o alta matrice B, prin suplimentarea liniilor si coloanelor matricei A, astfel:
, se poate genera o alta matrice B, prin suplimentarea liniilor si coloanelor matricei A, astfel:
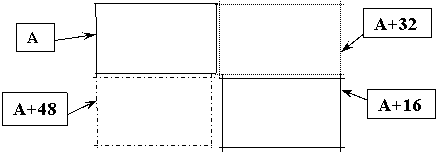
Matricea B
va avea doua "linii" si doua "coloane"
"Elementul" B(1,1) este matricea A;
"Elementul" B(1,2) este format din elementele matricei A, la care se aduna scalarul 32;
"Elementul" B(2,1) este format din elementele matricei A, la care se aduna scalarul 48;
"Elementul" B(2,1) este format din elementele matricei A, la care se aduna scalarul 16.
Pentru a realiza acest
deziderat, in linia de comanda (considerand ca matricea A este stocata in memorie), se
introduce, de la tastatura, urmatoarea secventa:
» A=[21,4,8,2;7,9,0,8;6,7,8,9;3,5,7,9];
» B
= [A, A+32; A+48, A+16]
 B =
B =
21 4 8 2 53 36 40 34
7 9 0 8 39 41 32 40
6 7 8 9 38 39 40 41
3 5 7 9 35 37 39 41
69 52 56 50 37 20 24 18
55 57 48 56 23 25 16 24
54 55 56 57 22 23 24 25
51 53 55 57 19 21 23 25
Un alt exemplu, asamblarea acelorasi
matrici, prin aranjarea acestora "in coloana" :
»B1 = [A ;A+32; A+48; A+16]
B1
=
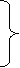 21 4 8 2
21 4 8 2
7 9 0 8
6 7 8 9
3 5 7 9
 53 36 40 34
53 36 40 34
39 41 32 40
38 39 40 41
35 37 39 41
 69 52 56 50
69 52 56 50
55 57 48 56
54 55 56 57
51 53 55 57
 37 20 24 18
37 20 24 18
23 25 16 24
22 23 24 25
19 21 23 25
STERGEREA LINIILOR SI A COLOANELOR
Se pot sterge
linii si coloane, ale unei matrici, folosind operatorul [ ]. De exemplu, pentru a sterge coloana 2 a
matricei A, data in forma algebrica generala:
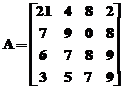 , se poate folosi urmatoarea secventa:
, se poate folosi urmatoarea secventa:
» A=[21,4,8,2;7,9,0,8;6,7,8,9;3,5,7,9];x=A;
x(:,2)=[]
se obtine o noua matrice x
:
x =
21 8 2
7 0 8
6 8 9
3 7 9
Pentru stergerea unui singur
element (de exemplu, tot al treilea element sa fie sters, considerand
elementele matricei scrise "pe coloana") se poate folosi urmatoarea secventa:
» A=[21,4,8,2;7,9,0,8;6,7,8,9;3,5,7,9];x=A;
» x(1:3:16) =[]
x =
7 6 4 9 5 8 8 7 8 9
Se observa
ca, elementele matricei au fost "citite" pe coloana, si tot al
treilea element, incepand cu primul, a fost eliminat, rezultatul fiind un
vector linie.
Extragerea
submatricilor prin indici
Elementele individuale ale unei matrici se
apeleaza cu numele acesteia, urmat de doi indici, cuprinsi intre
paranteze rotunde separati prin virgula. Primul indice semnifica linia, iar al doilea coloana
in care se gaseste elementul apelat. De exemplu, considerand matricea 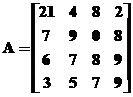 stocata in
memoria calculatorului, atunci cu instructiunea:
stocata in
memoria calculatorului, atunci cu instructiunea:
» A=[21,4,8,2;7,9,0,8;6,7,8,9;3,5,7,9];A(6,5)=A(1,2)+A(3,1) [Enter]
se obtine o alta matrice la care elementul din linia 6, coloana 5: A(6,5), al matricei A, este obtinut ca suma dintre elementul
de pe linia 1 -coloana 2 (A(1,2))
si elementul de pe linia 3, coloana 1 (A(3,1)), celelalte
elemente fiind inlocuite cu valoarea zero:
A =
21 4 8 2 0
7 9 0 8 0
6 7 8 9 0
3 5 7 9 0
0 0 0 0 0
0 0 0 0 10
Indicii pot fi scalari sau vectori. Indicii
vectori permit definirea unor submatrici, procedeu prin care se pot referi
parti disparate dintr-o matrice. Spre exemplu, daca se presupune
ca matricea M6x10 exista deja salvata pe disc,
»M=[1,2,3,4,5,6,7,8,9,10;-1,2,3,-4,5,-6,7,-8,9,-10;0,2,0,4,0,6,0,8,0,10;
-1,2,-3,4,-5,6,-7,8,-9,10;1,2,3,0,0,0,7,8,9,10;10,9,8,7,6,5,4,3,2,1];
M =
1 2 3 4 5 6 7 8 9 10
-1 2 3 -4 5 -6 7 -8 9 -10
0 2 0 4 0 6 0 8 0 10
-1 2 -3 4 -5 6 -7 8 -9 10
1 2 3 0 0 0 7 8 9 10
10 9 8 7 6 5 4 3 2 1
atunci, cu instructiunea urmatoare, se extrage submatricea B cu dimensiunea 5x1, formata cu elementele liniilor 1, 2, 3, 4, 5
(notatia "1:5" arata
ca sunt apelate toate liniile: 1
pana la 5) si coloana a 3-a a matricei M:
»B1=M(1:5,3) [Enter]
B1 =
3
3
0
-
3
3
in timp ce, instructiunea
urmatoare, extrage submatricea C,
de dimensiunea 5x4, constituita
din elementele primelor 5 liniii
si ale ultimelor 4 coloane
(coloanele 7, 8, 9, 10) ale matricei
M:
»C1=M(1:5, 7:10) [Enter]
C1
=
7 8 9 10
7 -
8 9 - 10
0 8 0 10
-7 8 - 9 10
7 8 9 10
Utilizarea, numai a caracterului ":" ("doua puncte") in locul
indicilor pentru linii sau pentru
coloane, presupune considerarea tuturor elementelor pe linii, respectiv pe
coloane. Astfel instructiunea:
»D1=M(:,3) [Enter]
extrage din matricea M, o
submatrice D1 cu elementele extrase
din matricea M
(toate liniile si numai coloana 3) avand
urmatoarea configuratie:
»D1
=
3
3
0
-
3
3
8
in timp ce, instructiunea:
»E1=M(1:5,:) [Enter]
extrage submatricea E1 care
contine liniile de la 1 la 5 ale tuturor coloanelor matricei M:
»E1
=
1 2 3 4 5 6 7 8 9 10
-1 2 3 -4 5 -6 7 -8 9 -10
0 2 0 4 0 6 0 8 0 10
-1 2 -3 4 - 5 6 -7 8 -9 10
1 2 3 0 0 0 7 8 9 10
UTILIZAREA SIMBOLURILOR
matlab, in variantele recente foloseste Symbolic Math Toolbox
(grup de instrumente matematice simbolice) pentru crearea variabilelor si
obiectelor simbolice. Aceasta colectie de instrumente MATLAB, nu
trebuie confundata cu facilitatea oferita, tot de MATLAB, pentru
utilizarea simbolurilor literale.
In calcule ingineresti se
utilizeaza frecvent, in locul expresiilor numerice, supradimensionate, in
general in cazul calculelor numerice cu matrici si de analiza
numerica, expresii simbolice. Nucleul computational este format pe
baza kernel-ului MAPLE®, dezvoltat la University of Waterloo, Canada, si la
Eidgenössiche Technische Hochschule, Zürich, Elvetia. Sunt disponibile
doua categorii de toolbox-uri: o
colectie de baza, numita Symbolic Math Toolbox, respectiv, o
colectie de functii extinse, numita Extended Symbolic Math
Toolbox.
Simbolurile matematice
se creeaza cu functia MATLAB sym(),
respectiv cu functia syms. Diferenta dintre aceste doua
functii consta in faptul ca prima creeaza o variabila
simbolica, in timp ce, a doua, creaza o multime finita de
variabile, prin declararea acestora, la inceputul sesiunii de lucru. Trebuie
facuta o diferentiere exacta intre simbolurile literale (ale literelor din alfabetul grecesc, de
exemplu) si simbolurile matematice folosite pentru reprezentarea variabilelor
in MATLAB. De exemplu, pentru introducerea unui text, de la tastatura, in
care intervin simboluri matematice sau caractere grecesti, precum si
caractere speciale folosite ca simboluri pentru operatori matematici, se
folosesc proprietatile disponibile in MATLAB, pentru inserarea
acestora. In tabelul alaturat sunt cuprinse toate simbolurile literale
si caracterele speciale, pentru care MATLAB ofera
facilitati de inserare in text:
|
Denumirea
simbolului
|
Simbol
|
Denumirea
simbolului
|
Simbol
|
Denumirea
simbolului
|
Simbol
|
|
alpha
|

|
upsilon
|
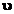
|
sim
|
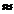
|
|
beta
|

|
phi
|
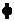
|
leq
|
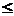
|
|
gamma
|
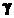
|
chi
|
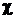
|
infty
|

|
|
delta
|

|
psi
|
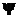
|
leftrightarrow
|
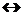
|
|
epsilon
|
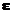
|
omega
|

|
leftarrow
|
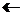
|
|
zeta
|
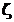
|
Gamma
|
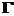
|
rightarrow
|
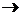
|
|
eta
|
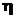
|
Delta
|
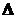
|
uparrow
|
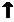
|
|
theta
|
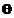
|
Theta
|
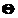
|
downarrow
|
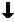
|
|
vartheta
|

|
Lambda
|

|
circ
|
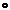
|
|
iota
|
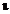
|
Xi
|
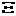
|
pm
|
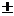
|
|
kappa
|

|
Pi
|
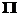
|
geq
|
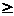
|
|
lambda
|
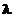
|
Sigma
|
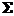
|
partial
|
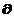
|
|
mu
|
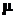
|
Upsilon
|
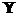
|
div
|
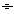
|
|
nu
|
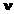
|
Phi
|
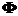
|
neq
|
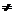
|
|
xi
|

|
Psi
|
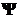
|
equiv
|
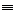
|
|
pi
|
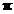
|
Omega
|
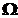
|
Im
|
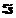
|
|
rho
|
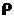
|
forall
|
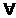
|
Re
|
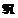
|
|
sigma
|
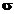
|
exists
|
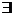
|
supset
|

|
|
varsigma
|
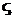
|
ni
|
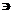
|
subset
|
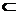
|
|
tau
|
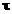
|
cong
|
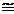
|
int
|
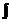
|
|
nabla
|
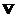
|
copyright
|
|
in
|
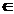
|
|
perp
|
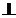
|
langle
|
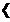
|
rangle
|
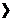
|
|
cap
|
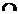
|
cup
|
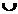
|
supseteq
|
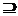
|
|
otimes
|
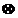
|
oplus
|
|
oslash
|
|
Introducerea
simbolurilor literale, respectiv a caracterelor speciale, in texte sau
siruri de caractere este o operatiune distincta a MATLAB, din
acest motiv, aceasta va fi tratata intr-o sectiune consacrata
acestui subiect. Ratiunea pentru care aceste observatii, referitoare
la diferenta dintre simbolurile matematice, folosite in MATLAB ca orice
alt tip de variabila si simbolurile literale, folosite ca siruri
de caractere (text) rezida in aceea ca se doreste eliminarea
unei posibilitati de aparitie a confuziilor nedorite, in tratarea
calculului simbolic.
Definirea si crearea expresiilor
simbolice
Variabilele
si expresiile simbolice se definesc cu comanda sym, in linia de comanda a spatiului de lucru MATLAB.
Functia MATLAB sym(x), permite
atribuirea, variabilei "x",
caracterul de "simbol". Astfel, cu comanda:
»c = sym('variabila_simbolica')
se creaza
variabila simbolica " c ", care va
afisa, atunci cand este accesata, expresia " variabila_simbolica ":
c =
variabila_simbolica
O expresie matematica poate fi
reprezentata printr-un simbol alfanumeric, fiind posibila utilizarea
acesteia, ulterior, in calcule si expresii numerice complexe. De exemplu,
presupunand ca se doreste folosirea repetata a unei expresii
matematice, relativ complicata, ca editare, in expresii diferite, atunci
se poate folosi urmatorul algoritm: se declara
expresia simbolica, dupa care aceasta se poate utiliza in calcule
si expresii ca o valoare
numerica sau simbolica de sine-statatoare. Fie expresia:
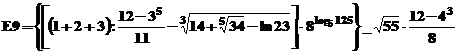
Declararea
acesteia ca variabila simbolica se realizeaza cu comanda:
»E=sym( ' (((1+2+3)/((12-3^5)/11)-(14+(34)^(1/5)-
log(23))^(1/3))*8 .
^((log(125))/(log(5))))-sqrt(55)*(12-4^3)/(8)
' )
ceea ce are ca
rezultat afisarea expresiei simbolice:
E =
(((1+2+3)/((12-3^5)/11)-(14+(34)^(1/5)-
log(23))^(1/3))*8^((log(125))/(log(5))))-sqrt(55)*(12-4^3)/(8)
Utilizarea acestei
expresii, in calcule, (pentru determinarea valorii expresiei f=E^2-3*E+log(E), de exemplu), este
posibila, folosind urmatoarea secventa MATLAB:
»
f=E^2-3*E+log(E)
f
=((-2/7-(14+34^(1/5)- log(23))^(1/3))*8^(log(125)/log(5))+
13/2*55^(1/2))^2-3*(-2/7-(14+34^(1/5)-log(23))^(1/3))*8^(log(125)/
log(5))-39/2*55^(1/2)+log((-2/7-(14+34^(1/5)-log(23))^(1/3))*
8^(log(125)/log(5))+13/2*55^(1/2))
Pentru ca operatiile aritmetice
cu expresii simbolice, in MATLAB, sa se poata realiza, este
necesara declararea tuturor variabilelor dintr-o expresie matematica.
De exemplu, rezolvarea unei ecuatii parametrice, cu parametrul " a ", si variabila " x ", declarata, este posibila daca, in prealabil,
s-a declarat simbol, parametrul respectiv, folosind, pentru aceasta
functia syms. Astfel, pentru
rezolvarea ecuatiei 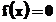 , unde
, unde 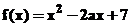 , se procedeaza astfel:
, se procedeaza astfel:
»syms
x a
»f=x^2-2*a*x+7
f
=
x^2-2*a*x+7
»
solve(f)
ans
=
[ a+(a^2-7)^(1/2)]
[
a-(a^2-7)^(1/2)]
elementele
matricei "simbolice" "ans" fiind
cele doua radacini ale ecuatiei date.
CALCULE SIMBOLICE
Diferentierea
Pentru calculul diferentialei
unei functii, se procedeaza astfel:
-se
declara simbolurile care urmeaza a fi utilizate:
»
syms x a b c
»
f=a*x^3+b*x^2+c*x
f
=
a*x^3+b*x^2+c*x
-se
aplica functia diff() expresiei simbolice, creata
anterior, "f":
»
diff(f)
ans =
3*a*x^2+2*b*x+c
Diferentiala se calculeaza,
implicit, in raport cu variabila "x",
indiferent de ordinea declararii simbolurilor. Daca, de exemplu, se
cere diferentiala in raport cu o alta variabila, atunci
functia MATLAB pentru calculul diferentialei se apeleaza cu doi
parametri:
»
diff(f,a)
ans
=
x^3
In mod similar se determina
diferentiala de ordinul "n"(n≥2)
in raport cu o variabila. Functia MATLAB diff() se apeleaza, atunci, cu doi sau trei parametri, intre
acestia, ultimul parametru fiind ordinul de diferentiere:
»diff(f,x,2)
ans
=
6*a*x+2*b
-diferentiala de ordinul doi in raport cu "x"
»
diff(f,2)
ans
=
6*a*x+2*b
- diferentiala de ordinul doi in raport cu "x"
»
diff(f,3)
ans
=
6*a
- diferentiala de ordinul trei in raport cu "x"
»
diff(f,a,2)
ans
=
diferentiala
de ordinul doi in raport cu "a"
Diferentiala matricei se
determina in mod similar diferentialelor functiilor simple:
»
syms x k pi
»
A=[ (k*x)^2, (pi*x)^3;k^2*x, (x^2+1)^(1/2)];
»
diff(A)
ans
=
[ 2*k^2*x, 3*pi^3*x^2]
[
k^2, 1/(x^2+1)^(1/2)*x]
Derivatele partiale se
determina folosind functia MATLAB jacobian(), in functie de variabilele functiilor. Astfel,
derivata unei functii 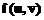 , in raport cu functiile
, in raport cu functiile 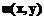 , respectiv
, respectiv 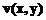 , se determina cu urmatoarea secventa:
, se determina cu urmatoarea secventa:
»
syms x y u v
»
u=2*x^4-log(x^2+4);v=exp(x^2-8)+4*log(3*x^3-2);
»
Der_partiala=jacobian([u;v],[x,y])
Der_partiala =
[8*x^3-2*x/(x^2+4)-(2*x+2*y^3)/(x^2+2*x*y^3-5*y),- (6*x*y^2-5)/(x^2+2*x*y^3-5*y)]
[ 2*x*exp(x^2-8*y^3+6*y^2)+36*x^2/(3*x^3-2*y),(-24*y^2+12*y)*exp(x^2-8*y^3+6*y^2)-8/(3*x^3-2*y)]
respectiv, pentru
alte doua functii:
» syms x y u v a b c d
»
u=cos(a*x+b*y);v=sin(c*x-d*y);
»
Der_partiala=jacobian([u;v],[x,y])
Der_partiala =
[
-sin(a*x+b*y)*a, -sin(a*x+b*y)*b]
[ cos(c*x-d*y)*c, -cos(c*x-d*y)*d]
Calculul limitelor functiilor
simbolice
Calculul limitei unei functii,
definita simbolic presupune existenta, in primul rand, limitei
functiei respective intr-un punct. Intrucat se definesc limitele laterale
(la stanga sau la dreapta), MATLAB permite calculul diferentiat al
acestora prin specificarea "sensului" de calcul. Limitele se calculeaza
folosind functia MATLAB limit(f(x),xo),
cu parametrii de intrare, f(x) si
xo in functie de
tipul limitei. De exemplu, daca se cere calculul limitei functiei 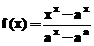 , cand x tinde
spre a, se procedeaza astfel:
, cand x tinde
spre a, se procedeaza astfel:
»syms
a x
»limit((x^x-a^x)/(a^x-a^a),a)
ans
=
1/log(a)
Pentru
calculul limitei sirului 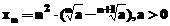 , se foloseste secventa MATLAB:
, se foloseste secventa MATLAB:
»syms n a
» limit((n^2)*(a^(1/n)-a^(1/(n+1))),n,inf)
ans =
log(a)
Limitele
laterale se determina folosind aceeasi functie MATLAB, pentru
care paramatrii de intrare sunt:functia (scrisa simbolic), variabila,
punctul in care se cere limita respectiv "sensul" ("left"-stanga;
"right"-dreapta), dupa cum limita se calculeaza, la stanga, sau la
dreapta punctului de acumulare. De exemplu, pentru calculul limitelor laterale 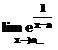 si
si 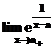 se procedeaza
astfel:
se procedeaza
astfel:
»syms
a x
» limit(exp(1/(x-a)),x,a,'left')
ans =
0
» limit(exp(1/(x-a)),x,a,'right')
ans =
inf
Calculul sumelor simbolice
Pentru
calculul sumelor de tipul 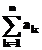 , in care sirul
, in care sirul 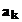 este definit
este definit
simbolic, se
foloseste functia MATLAB symsum(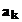 ,k,ko,kn).
De exemplu, pentru calculul sumei
,k,ko,kn).
De exemplu, pentru calculul sumei 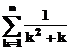 , se foloseste secventa:
, se foloseste secventa:
»
syms k n
»
symsum(1/(k^2+k),1,n)
ans
=
-1/(n+1)+1
In cazul in care indexul de sumare
nu este implicit (in expresia simbolica, sirul fiind definit cu mai
multe variabile), functia MATLAB trebuie sa fie explicit definita
prin parametrii de intrare. Astfel, daca se cere calculul sumelor infinite
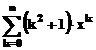 si
si 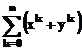 , se foloseste secventa:
, se foloseste secventa:
» syms k x y n
»symsum((x^k)*(k^2+1),k,0,inf)
ans =
-(2*x^2-x+1)/(x-1)^3
respectiv, pentru cea de-a doua suma:
» syms k x y n
»symsum(x^k+y^k,k,0,inf)
ans =
-1/(x-1)-1/(y-1)
Calculul
seriilor Taylor
Dezvoltarea unei functii in
serie Taylor
are o aplicabilitate deosebita in calculele numerice. Fie 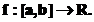 Se pune problema
determinaii unei functii F,
care sa aproximeze functia f
in intervalul [a,b]. Se recurge la
aceasta aproximare in doua cazuri: 1) cand nu se cunoaste
expresia analitica a lui f, dar
se cunosc valorile sale intr-un numar finit de puncte si 2) cand
expresia analitica a lui f este destul de complicata si
cu ajutorul acesteia calculele sunt destul de dificile. Pentru evaluarea lui f(x) se cauta o alta
functie F(x) relativ
simpla astfel ca pentru orice valoare a lui x valoarea lui f(x) se
alege dintr-o anumita clasa de functii, de exemplu din clasa
polinoamelor de grad n sau mai mic,
pentru un anume n, atunci trebuie ca
F(x) sa ia aceeasi valoare
cu f(x) pentru anumite valori ale
lui x. Aceste valori ale lui x sunt adesea referite ca puncte de
interpolare. De asemenea se poate cere ca anumite derivate ale lui F(x) sa ia acelasi valori cu
valorile derivatelor corespunzatoare ale lui f(x) in anumite puncte de interpolare. Se poate arata ca
daca F(x) este suma a n+1 termeni ai seriei Taylor pentru f(x) in punctul x=a, atunci F(x) poate fi considerata ca un
polinom de interpolare pentru f(x)
de grad n sau mai mic, deoarece:
Se pune problema
determinaii unei functii F,
care sa aproximeze functia f
in intervalul [a,b]. Se recurge la
aceasta aproximare in doua cazuri: 1) cand nu se cunoaste
expresia analitica a lui f, dar
se cunosc valorile sale intr-un numar finit de puncte si 2) cand
expresia analitica a lui f este destul de complicata si
cu ajutorul acesteia calculele sunt destul de dificile. Pentru evaluarea lui f(x) se cauta o alta
functie F(x) relativ
simpla astfel ca pentru orice valoare a lui x valoarea lui f(x) se
alege dintr-o anumita clasa de functii, de exemplu din clasa
polinoamelor de grad n sau mai mic,
pentru un anume n, atunci trebuie ca
F(x) sa ia aceeasi valoare
cu f(x) pentru anumite valori ale
lui x. Aceste valori ale lui x sunt adesea referite ca puncte de
interpolare. De asemenea se poate cere ca anumite derivate ale lui F(x) sa ia acelasi valori cu
valorile derivatelor corespunzatoare ale lui f(x) in anumite puncte de interpolare. Se poate arata ca
daca F(x) este suma a n+1 termeni ai seriei Taylor pentru f(x) in punctul x=a, atunci F(x) poate fi considerata ca un
polinom de interpolare pentru f(x)
de grad n sau mai mic, deoarece:
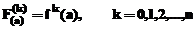
Forma generala a dezvoltarii
functiei f(x), in serie Taylor, in jurul unui
punct x=a este: 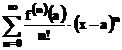 . Functia MATLAB, pentru calculul primilor n termeni ai dezvoltarii, se
utilizeaza functia taylor(f(x), n, a). De exemplu, pentru
determinarea primilor 4 termeni ai dezvoltarii
functiei
. Functia MATLAB, pentru calculul primilor n termeni ai dezvoltarii, se
utilizeaza functia taylor(f(x), n, a). De exemplu, pentru
determinarea primilor 4 termeni ai dezvoltarii
functiei 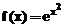 , in jurul punctului
x=3, se va folosi urmatoarea secventa:
, in jurul punctului
x=3, se va folosi urmatoarea secventa:
»
syms x
»
taylor(exp(x^2),4,3)
ans
=
exp(9)+6*exp(9)*(x-3)+19*exp(9)*(x-3)^2+42*exp(9)*(x-3)^3
Problemele legate de aproximarea
folosind seriile Taylor
vor fi abordate intr-o alta sectiune a acestei lucrari.


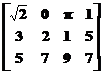 ; E=[1 3 5 7]
; E=[1 3 5 7]
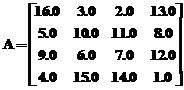 ,
, 
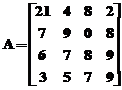 , se poate genera o alta matrice B, prin suplimentarea liniilor si coloanelor matricei A, astfel:
, se poate genera o alta matrice B, prin suplimentarea liniilor si coloanelor matricei A, astfel:
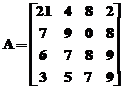 , se poate folosi urmatoarea secventa:
, se poate folosi urmatoarea secventa: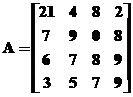 stocata in
memoria calculatorului, atunci cu instructiunea:
stocata in
memoria calculatorului, atunci cu instructiunea: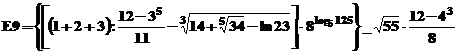
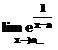 si
si 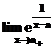 se procedeaza
astfel:
se procedeaza
astfel: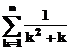 , se foloseste secventa:
, se foloseste secventa: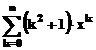 si
si 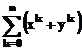 , se foloseste secventa:
, se foloseste secventa: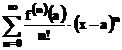 . Functia MATLAB, pentru calculul primilor n termeni ai dezvoltarii, se
utilizeaza functia
. Functia MATLAB, pentru calculul primilor n termeni ai dezvoltarii, se
utilizeaza functia