Notiuni aprofundate de programare

Metode si strategii de proiectare a algoritmilor (alias tehnici de programare)

In rezolvarea sa cu ajutorul calculatorului orice problema trece prin trei etape obligatorii: Analiza problemei, Proiectarea algoritmului de solutionare si Implementarea algoritmului intr-un program pe calculator. In ultima etapa, sub acelasi nume, au fost incluse in plus doua subetape cunoscute sub numele de Testarea si Intretinerea programului. Aceste subetape nu lipsesc din "ciclul de viata" a oricarui produs-program ce "se respecta" dar , pentru simplificare, in continuare ne vom referi doar la cele trei mari etape..

Daca etapa implementarii algoritmului intr-un program executabil este o etapa exclusiv practica, realizata "in fata calculatorului", celelalte doua etape au un caracter teoretic pronuntat. In consecinta, primele doua etape sint caracterizate de un anumit grad de abstractizare. Din punct de vedere practic si in ultima instanta criteriul decisiv ce confera succesul rezolvarii problemei este dat de calitatea implementarii propriuzise. Mai precis, succesul solutionarii este dat de performantele programului: utilitate, viteza, fiabilitate, manevrabilitate, lizibilitate, etc. Este imatura si neprofesionala "strategia" programatorilor incepatori care neglijind primele doua etape sar direct la a treia, fugind de analiza si de componenta abstracta a efortului de solutionare. Ei ofera cu totii aceeasi justificare: "Eu nu vreau sa mai pierd vremea cu . , am sa fac programul cum stiu eu. Pina cind nu o sa faca cineva altul mai bun decit al meu, pina atunci . nu am cu cine sta de vorba !".

Este adevarat ca ultima etapa in rezolvarea unei probleme - implementarea - este intr-adevar decisiva si doveditoare, dar primele doua etape au o importanta capitala. Ele sint singurele ce pot oferi raspunsuri la urmatoarele intrebari dificile: Avem certitudinea ca solutia gasita este corecta ? Avem certitudinea ca problema este complet rezolvata ? Cit de eficienta este solutia gasita ? Cit de departe este solutia aleasa de o solutie optima ?

Sa mentionam in plus ca literatura de specialitate contine un numar impresionant de probleme "capcana" pentru incepatori si nu numai. Ele sint toate inspirate din realitatea imediata dar pentru fiecare dintre ele nu se cunosc solutii eficiente in toata literatura de profil. Exista printre ele chiar unele probleme extrem de dificile pentru care s-a demonstrat riguros ca nu admit solutie cu ajutorul calculatorului. (Mai precis, s-a demonstrat ca ele nu admit solutie prin metode algoritmice, in spiritul tezei Turing-Church). Citi dintre programatorii incepatori n-ar fi surprinsi sa afle ca problema "atit de simpla" (ca enunt) a carei solutionare tocmai au abandonat-o este de fapt o problema dovedita ca fiind intratabila sau chiar insolvabila algoritmic ? Partea proasta a lucrurilor este ca, asa cum ciupercile otravite nu pot fi cu usurinta deosebite de cele comestibile, tot astfel problemele netratabile pot fi cu usurinta confundate cu niste probleme usoare la o privire rapida si lipsita de experienta.

Sa intelegem mai intii care este "cheia" ce conduce la raspunsuri pentru intrebarile de mai sus iar apoi vom trece la prezentarea metodelor clasice de proiectare a solutiilor. Aceste metode de proiectare a algoritmilor-solutie sint cunoscute in literatura de specialitate sub numele de tehnici de programare si sint considerate metode sau instrumente soft eficiente si cu arie larga de actiune.

Daca ar fi sa sintetizam in cite un cuvint efortul asupra caruia se concentreaza fiecare din primele doua etape - analiza si proiectarea - acestea ar fi: corectitudine si eficienta. Etapa de analiza este singura care permite dovedirea cu argumente riguroase a corectitudinii solutiei, iar etapa de proiectare este singura care poate oferi argumente precise in favoarea eficientei solutiei propuse.

In general problemele de informatica au in forma lor initiala sau in enunt o caracteristica pragmatica. Ele sint foarte ancorate in realitatea imediata si aceasta le confera o anumita asemanare. Totusi ele au in forma initiala un grad mare de eterogenitate, diversitate si lipsa de rigoare. Fiecare dintre aceste atribute "negative" este un obstacol major pentru demonstrarea corectitudinii solutiei. Rolul esential al etapei de analiza este deci acela de a transfera problema "de pe nisipurile miscatoare" ale realitatii imediate de unde ea provine intr-un plan abstract, adica de a o modela. Acest "univers paralel" este dotat cu mai multa rigoare si disciplina interna, avind legi precise, si poate oferi instrumentele logice si formale necesare pentru demonstrarea riguroasa a corectitudinii solutiei problemei.

Planul abstract in care sint "transportate" toate problemele este planul sau universul obiectelor matematice. Acest univers al matematicii este unanim acceptat (de ce ?!) iar corespondentul problemei in acest plan va fi modelul matematic abstract asociat problemei. Demonstrarea corectitudinii proprietatilor ce leaga obiectele universului matematic a fost si este sarcina matematicienilor. Celui ce analizeaza problema din punct de vedere informatic ii revine sarcina (nu tocmai usoara) de a dovedi printr-o demonstratie constructiva ca exista o corespondenta precisa (bijectiva) intre partile componente ale problemei reale, "dezasamblata" in timpul analizei, si partile componente ale modelului abstract asociat. Odata descoperita, formulata precis si dovedita, aceasta "perfecta oglindire" a problemei reale in planul obiectelor matematice ofera certitudinea ca toate proprietatile si legaturile ce exista intre subansamblele modelului abstract se vor regasii precis (prin reflectare) intre partile interne ale problemei reale, si invers. Atunci, solutiei abstracte descoperita cu ajutorul modelului matematic abstract ii va corespunde o solutie reala concretizata printr-un algoritm ce poate fi implementat intr-un program executabil.

Aceasta este calea generala de rezolvare a problemelor si orice poate verifica. Ca si exercitiu, sa se demonstreze corectitudinea (sa se aduca argumente precise, clare si convingatoare in favoarea corectitudinii) metodei de extragere a radicalului invatata inca din scoala primara sau a algoritmului lui Euclid de determinare a celui mai mare divizor comun a doua numere prin impartiri intregi repetate. Argumentele elevilor de forma: "Este corect pentru ca asa ne-a invatat doamna profesoara!" sau "Este corect pentru ca asa face toata lumea !" sint "normale" atit timp cit nu li se ofera o argumentatie matematica riguroasa.

Ideea centrala a etapei a doua - proiectarea uni algoritm de solutionare eficient poate fi formulata astfel: din studiul proprietatilor si limitelor modelului matematic abstract asociat problemei se deduc limitele inferioare ale complexitatii minimale ("efortului minimal obligatoriu") inerente oricarui algoritm ce va solutiona problema in cauza. Complexitatea interna a modelului abstract si complexitatea solutiei abstracte se va reflecta imediat asupra complexitatii reale a algoritmului, adica asupra eficientei, de solutionare a problemei. Acest fapt permite prognosticarea inca din aceasta faza - faza de proiectare a algoritmului de solutionare - a eficientei practice, masurabila ca durata de executie, a programului.

Aceasta corespondenta exacta intre complexitatea modelului abstract si complexitatea algoritmului de solutionare ofera cheia unor demonstratii riguroase a imposibilitatii existentei solutiei prin metode algoritmice pentru o lista intreaga de probleme (cum ar fi de exemplu Problema a 10-a a lui Hilbert, formulata inca din 1900).

Detailind cele prezentate deja, vom construi in continuare cadrul teoretic general pentru intelegerea strategiilor de proiectare a algoritmilor.

Cresterea impresionanta a puterii de calcul a calculatoarelor i-a "obligat" pe informaticienii ultimilor treizeci de ani sa nu se mai eschiveze de la abordarea problemelor dificile cu caracter algoritmic din diverse domenii care au intrat in atentia matematicienilor inca de la inceputul acestui secol. De altfel, astfel de probleme cu solutii algoritmice nu constituiau neaparat o noutate pentru matematicienii inceputului de secolul. Inca de pe vremea lui Newton matematicienii si-au pus, de exemplu, problema descoperirii unor metode precise (adica algoritmi!) de determinare in pasi de aproximare succesiva a solutiei unei ecuatii ce nu poate fi rezolvata prin radicali. Dar "boom-ul" dezvoltarii tehnicii de calcul din a doua jumatate a secolului a creat posibilitatea abordarii unor probleme cheie pentru anumite domenii strategice (de exemplu, controlul si dirijarea satelitilor pe orbita, probleme de planificare sau optimizare in economie, etc.) care se reduc in fapt la solutionarea eficienta a unor probleme de optimizare matematica prin metode iterative (algoritmi).

Spre deosebire de aceste probleme a caror succes in solutionare a fost total si cu consecintele ce se vad, exista insa o serie de probleme dificile inspirate din realitate care se cer imperios rezolvate eficient cu ajutorul calculatorului.

Principala caracteristica a acestora este ca, datorita generalitatii lor sau datorita dificultatii "ascunse", in literatura de specialitate nu exista metode iterative eficiente de rezolvare a lor si nu se stie daca ele admit astfel de solutii. Singurul fapt ce poate fi stabilit dinainte in cazul solutionarii unor astfel de probleme este "spatiul" in care solutia trebuie cautata. Ceea ce trebuie atunci construita este o strategie corecta si cit mai generala de cautare a solutiei (solutiilor) in acel spatiu de cautare a solutiilor.

Exemplu concret: exista o clasa intreaga de probleme ce cer implicit sa se genereze toate obiectele unei multimi (cum ar fi problema generarii tuturor permutarilor unei multimi cu n elemente). In acest caz este cunoscuta dinainte proprietatea ce trebuie sa o indeplineasca fiecare solutie ca sa fie un obiect al spatiului de cautare a solutiilor. Efortul de solutionare va fi redus atunci la aflarea, cautarea sau generarea pe baza proprietatii respective a tuturor obiectelor posibile, fara insa a lasa vreunul pe dinafara.

Modelul matematic abstract cel mai general care permite modelarea acestui tip de probleme este graful. Un graf este un obiect matematic riguros care, simplificat, poate fi privit ca fiind o diagrama formata din noduri unite prin sageti (muchii). De exemplu, orice harta feroviara sau rutiera poate fi privita ca un graf cu multimea nodurilor formata din localitati iar multimea muchiilor formata din rutele de transport directe dintre localitatile respective. Graful permite descrierea legaturilor si a relatiilor ce exista intre diferite obiecte abstracte reprezentate prin noduri. Experienta arata ca acest model matematic abstract este cel mai general si cel mai potrivit pentru descrierea unui spatiu de cautare a solutiilor unei probleme. In cazul spatiului de cautare, nodurile sint solutiile posibile (ipotetice). Doua noduri in graf vor fi unite prin sageti (muchii) daca cele doua solutii posibile au in comun o aceeasi proprietate. Muchiile grafului sint "puntile" ce vor permite algoritmului trecerea de la un nod la altul, de la o solutie ipotetica la alta, in timpul procesului de cautare a solutiei (sau a tuturor solutiilor). Rezulta ca strategiile cele mai generale de cautare a solutiei (solutiilor) pe modelul abstract asociat problemei sint reductibile la metodele generale de traversare a unui graf.

Ordinea de traversare a grafului determina precis arborele de traversare a grafului. Acest arbore este de fapt un subgraf particular al grafului initial, avind acelasi numar de noduri si ca radacina virful initial de pornire. Cele doua metode clasice de traversare a unui graf (cautare intr-un graf) poarta in literatura de specialitate numele: BreathFirstSearch (BFS) si DepthFirstSearch (DFS), respectiv Traversarea in latime (sau traversarea pe nivele) si Traversarea in adincime (traversarea "labirintica") a grafului. Ambele metode stau la baza celei mai cunoscute strategii de proiectare a algoritmilor (impropriu denumita tehnica de programare): BackTracking respectiv cautare (traversare) in spatiul de cautare a solutiilor (a grafului) cu revenire pe "urma" lasata.

Iata un exemplu de graf (7 noduri si 10 arce-sageti) si ordinea sa de traversare prin cele doua metode:

4 4 4

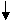
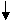
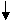
2 2 2

1 5 7 1 5 7 1 5 7

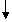
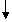
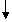
3 3 3

6 6 6

Ordinea de parcurgere a celor 7 virfuri ale grafului, tinind cont si de sensul dat de sageti, este in cazul DFS (in adincime): 1,2,4,5,6,3,7 asa cum se vede din arborele parcurgerii in adincime. Din fiecare nod se continua cu nodul (nevizitat inca) dat de prima alegere posibila: de exemplu, din 4 se continua cu 5 (ales in favoarea lui 7). Se poate observa cum din nodul 3, nemaiexistind continuare, are loc o revenire pe "pista lasata" pina in nodul 6 de unde se continua parcurgerea in adincime cu prima alegere posibila. In cazul BFS (in latime) ordinea de traversare este: 1,2,3,4,5,7,6 asa cum se poate vedea in arborele parcurgerii in latime. In aceasta situatie, dintr-un nod sint vizitati toti vecinii (nevizitati inca), iar apoi se face repeta acelasi lucru pentru fiecare nod vecin, in ordinea vizitarii. Se observa cum nodul 7 este vizitat inaintea nodului 6, fiind vecin cu nodul 4. (De fapt, aceasta se explica prin faptul ca distanta de la 1 la 7 este mai mica cu o unitate decit distanta de la 1 la 6.) Putem spune ca in cazul traversarii in latime ordinea de traversare este data de departarea nodurilor fata de nodul de start.

Iata cum arata procedura generala DepthFirstSearch (DFS) de traversare a unui graf descrisa in pseudo-cod in varianta recursiva:

Procedura DFS(v:nod);

Viziteaza v;

Marcheaza v; // v devine un nod vizitat //

Cit timp (exista w nemarcat nod adiacent lui v) executa DFS(w);

Sa nu uitam ca aceasta procedura poate fi privita ca "scheletul" pe care se construieste orice procedura backtracking recursiva

BackTracking.

Pentru a preciza mai exact in ce consta aceasta metoda, vom relua pe un exemplu concret cele spuse deja. Avem urmatoarea problema: se cere generarea tuturor permutarilor unei multimi de n elemente ce nu contin elementul x (dat dinainte) pe primele doua pozitii. Conform celor afirmate, este suficient sa "construim" modelul abstract - graful - (mai precis arborele) tuturor permutarilor celor n elemente. Apoi, printr-o parcurgere exhaustiva a nodurilor sale, prin una din metodele BFS sau DFS, sa pastram numai acele noduri ce verifica in momentul "vizitarii" conditia impusa (lipsa lui x de pe primele doua pozitii).

Observam ca aceasta metoda necesita folosirea in scopul memorarii dinamice a drumului parcurs (in timpul cautarii solutiei) a mecanismului de stiva, fapt sugerat chiar de numele ei: tracking, adica inregistrarea pistei parcurse. Acest mecanism de stiva, care permite atit memorarea pistei cit si revenirea - back-tracking-ul, este unul din mecanismele de baza ce este folosit pe scara larga in procedurile de gestiune dinamica a datelor in memorie. In plus, exista unele cazuri particulare de probleme in care solutia cautata se obtine in final prin "varsarea" intregului continut al stivei si nu doar prin "nodul" ultim vizitat, aflat in virful stivei.

Exemplul cel mai potrivit de problema ce necesita o strategie de rezolvare backtracking este Problema Labirintului: se cere sa se indice, pentru o configuratie labirintica data, traseul ce conduce catre iesirea din labirint. Iata un exemplu sugestiv:

Observati cum, dupa 15 pasi, este necesara o revenire (backtracking) pina la casuta 6, de unde se continua pe o alta pista. "Pista falsa" a fost memorata in stiva, element cu element, iar revenirea se va realiza prin eliminarea din stiva tot element cu element. Cind in virful stivei reapare casuta cu numarul 6, stiva incepe din nou sa creasca memorind elementele noului drum. In final stiva contine in intregime solutia: drumul corect catre iesirea din labirint.

In consecinta, indiferent de forma particulara ce o poate lua sau de modul in care este "citita" in final solutia, esentialul consta in faptul ca backtracking-ul este o metoda de programare ce contine obligatoriu gestiune de stiva. Lipsa instructiunilor, explicite sau "transparente", de gestionare a stivei intr-un program (de exemplu, lipsa apelului recursiv), este un indiciu sigur de recunoastere a faptului ca acel algoritm nu foloseste metoda sau strategia de rezolvare BackTracking.

Tot o metoda back-tracking este si metoda de programare cunoscuta sub numele programare recursiva. Ea este mai utilizata decit metoda clasica BackTracking, fiind mai economicoasa din punctul de vedere al minimizarii efortului de programare. Aceasta metoda se reduce la construirea, in mod transparent pentru programator, a arborelui apelurilor recursive, traversarea acestuia prin apelarea recursiva (repetata) si efectuarea actiunilor corespunzatoare in momentul "vizitarii" fiecarui nod al arborelui. Apelarea recursiva constituie "motorul vehiculului" de traversare si are doar rolul de a permite traversarea arborelui. Gestionarea stivei apelurilor recursive si revenirea - back-tracking-ul ramine in sarcina mediului de programare folosit si se efectueaza intr-un mod mascat pentru programator. Din acest punct de vedere, programatorului ii revine sarcina scrierii corecte a instructiunii de apel recursiv si a instructiunii ce "scurt-circuiteaza" bucla infinita a apelurilor recursive. Singurele instructiuni care "fac treaba", in sensul rezolvarii propriuzise a problemei respective, sint cele cuprinse in corpul procedurii.

De exemplu, iata cum arata in limbajul de programare Pascal procedura generala de generare a permutarilor in varianta recursiva si arborele de generare a permutarilor multimii (n=3), pe nivele:

Procedure Permut(k:byte;s:string); 

Var i:byte;tmp:char;

Begin

If k=n then begin

For i:=1 to n do Write(s[i]);

Write(';');

end else

For i:=k to n do begin

tmp:=s[i];s[i]:=s[k];s[k]:=tmp;

Permut(k+1,s);

end;

End;

Nivelele arborelui (rasturnat pe orizontala)

1 2 3

2 ---- 3 Fiecare nivel al arborelui corespunde unei pozitii in sirul permutarilor. Astfel, pe prima

1 <

3 ---- 2 pozitie (nivelul 1) pot fi oricare din cele trei elemente: 1, 2, 3. Pe pozitia urmatoare pot

/

1 ---- 3 fi oricare din celelalte doua elemente ramase: 2, 3; 1, 3; 1, 2. Pe al treilea nivel si ultimul

Start -- 2 <

3 ---- 1 vor fi numai elementele ramase (cite unul). Generarea permutarilor consta in construirea

1 ---- 2 si parcurgerea arborelui permutarilor: odata ajunsi cu parcurgerea la un capat din dreapta

3 <

2 ---- 1 vom afisa de fiecare data "drumul" de la "radacina" la "frunza" terminala.

Observam ca arborele permutarilor este identic cu arborele apelurilor recursive si ca controlul si gestiunea stivei se face automat, transparent fata de programator. Instructiunilor de control (din background) le revine sarcina de a pastra si de a memora, de la un apel recursiv la altul, string-ul s ce contine permutarile. Desi aceasta procedura recursiv de generare a permutarilor pare o varianta de procedura simpla din punctul de vedere al programatorului, in realitate, ea contine intr-un mod ascuns efortul de gestionare a stivei: incarcarea-descarcarea stringului s si a intregului k. Acest efort este preluat in intregime de instructiunile incluse automat de mediul de programare pentru realizarea recursivitatii.

Avantajul metodei back-tracking este faptul ca efortul programatorului se reduce la doar trei sarcini:

"construirea" grafului particular de cautare a solutiilor

adaptarea corespunzatoare a uneia din metodele generale de traversare-vizitare a grafului in situatia respectiva (de exemplu, prin apel recursiv)

adaugarea instructiunilor "ce fac treaba" care, fiind apelate in mod repetat in timpul vizitarii nodurilor (grafului solutiilor posibile), rezolva gradat problema, gasind sau construind solutia.

Actiunea de revenire ce da numele metodei, backtracking - revenire pe "pista lasata", este inclusa si este efectuata de subalgoritmul de traversare a grafului solutiilor posibile. Acest subalgoritm are un caracter general si face parte din "zestrea" oricarui programator. In cazul particular in care graful solutiilor este arbore, atunci se poate aplica intotdeauna cu succes metoda programarii recursive care conduce la un cod-program redus si compact.

Prezentam din nou procedura generala DepthFirstSearch (DFS) de traversare a unui graf in varianta recursiva (ce "construieste" de fapt arborele de traversare a grafului avind ca radacina nodul de pornire) pentru a pune in evidenta cele spuse.

Procedura DFS(v:nod);

Viziteaza v;

Marcheaza v; // v devine un nod vizitat //

Cit timp (exista w nemarcat nod adiacent lui v)

executa DFS(w); 

Exista situatii in care, la unele probleme, putem intilni solutii tip-backtracking fara insa a se putea sesiza la prima vedere prezenta grafului de cautare asociat si actiunea de traversare a acestuia, ci doar prezenta stivei. O privire mai atenta insa va conduce obligatoriu la descoperirea arborelui de cautare pe graful solutiilor, chiar daca el exista doar intr-o forma mascata. Acest fapt este inevitabil si constituie esenta metodei - cautare (generare) cu revenire pe pista lasata.

Back-tracking-ul, metoda generala si cu o larga aplicabilitate, fiind reductibila in ultima instanta la traversarea spatiului -grafului de cautare- a solutiilor, are marele avantaj ca determina cu certitudine toate solutiile posibile, cu conditia ca graful asociat de cautare a solutiilor sa fie corect. Dar ea are marele dezavantaj ca necesita un timp de executie direct proportional cu numarul nodurilor grafului de cautare asociat (sau numarul cazurilor posibile). In cele mai multe cazuri acest numar este exponential (eⁿ) sau chiar mai mare, factorial (n!), unde n este dimensiunea vectorului datelor de intrare. Acest fapt conduce la o durata de executie de marime astronomica facind intr-un astfel de caz algoritmul complet inutilizabil, chiar daca el este corect teoretic. (De exemplu, daca solutionarea problemei ar necesita generarea tuturor celor 100! permutari (n=100), timpul de executie al algoritmului depaseste orice imaginatie.) In astfel de situatii, in care dimensiunea spatiului de cautare-generare a solutiilor are o astfel de dependenta in functie de n (fiind o functie de ordin mai mare decit functia polinomiala), este absolut necesara imbunatatirea acestei metode sau inlocuirea ei. Nu este insa necesara (si de multe ori nici nu este posibila!) abandonarea modelului abstract asociat - graful solutiilor posibile, cu calitatile si proprietatile sale certe - ci este necesara doar obtinerea unei durate de executie de un ordin de marime inferior printr-o alta strategie de parcurgere a spatiului de cautare.

Greedy.

In strategia backtracking cautarea solutiei, adica vizitarea secventiala a nodurilor grafului solutiilor cu revenire pe urma lasata, se face oarecum "orbeste" sau rigid, dupa o regula simpla care sa poata fi rapid aplicata in momentul "parasirii" unui nod vizitat. In cazul metodei (strategiei) greedy apare suplimentar ideea de a efectua in acel moment o alegere. Dintre toate nodurile urmatoare posibile de a fi vizitate sau dintre toti pasii urmatori posibili, se alege acel nod sau pas care asigura un maximum de "cistig", de unde si numele metodei: greedy = lacom. Evident ca in acest fel poate sa scada viteza de vizitare a nodurilor - adica a solutiilor ipotetice sau a solutiilor partiale - prin adaugarea duratei de executie a subalgoritmului de alegere a urmatorului nod dupa fiecare vizitare a unui nod. Exista insa numerosi algoritmi de tip greedy veritabili care nu contin subalgoritmi de alegere. Asta nu inseamna ca au renuntat la alegerea greedy ci, datorita "scurtaturii" descoperite in timpul etapei de analiza a problemei, acei algoritmi efectueaza la fiecare pas o alegere fara efort si in mod optim a pasului (nodului) urmator. Aceasta alegere, dedusa in etapa de analiza, conduce la maximum de "profit" pentru fiecare pas si scurteaza la maximum drumul catre solutia cautata.

Aparent aceasta metoda de cautare a solutiei este cea mai eficienta, din moment ce la fiecare pas se trece dintr-un optim (partial) intr-altul. Totusi, ea nu poate fi aplicata in general ci doar in cazul in care exista certitudinea alegerii optime la fiecare pas, certitudine rezultata in urma etapei anterioare de analiza a problemei. Ori, dezavantajul este ca, la majoritatea problemelor dificile, etapa de analiza nu poate oferi o astfel de "pista optima" catre solutie. Un alt dezavantaj al acestei strategii este ca nu poate sa conduca catre toate solutiile posibile ci doar catre solutia optima (din punct de vedere a alegerii efectuate in timpul cautarii solutiei), dar poate oferi toate solutiile optime echivalente.

Programarea dinamica.

Este o metoda sau strategie ce isi propune sa elimine dezavantajele metodei recursive care, in ultima instanta, am vazut ca se reduce la parcurgerea in adincime a arborelui apelurilor recursive (adica backtracking). Aceasta metoda se apropie ca idee strategica de metoda Greedy, avind insa unele particularitati.

Pentru a o intelege este necesara evidentierea dezavantajului major al recursivitatii. El consta din cresterea exagerata si nerentabila a efortului de executie prin repetarea ineficienta a unor pasi. Urmarind arborele apelurilor recursive se observa repetarea inutila a unor cazuri rezolvate anterior, calculate deja inainte pe alta ramura a arborelui. Metoda eminamente iterativa, programarea dinamica elimina acest dezavantaj prin "rasturnarea" procedeului de obtinere a solutiei si implicit a arborelui apelurilor recursive. Printr-o abordare bottom-up (de la baza spre virf) ea reuseste sa elimine operatiile repetate inutil in cazul abordarii top-down (de la virf spre baza).

Cu totii am invatat ca, daca vrem sa calculam "cu mina" o combinare sau un tabel al combinarilor, in loc sa calculam de fiecare data combinari de n luate cite k pe baza definitiei recursive: C(n,k)=C(n-1,k-1)+C(n-1,k) cind n,k>0, sau, C(n,k)=1 cind k=0 sau n=k, este mult mai eficient sa construim Triunghiul lui Pascal, pornind de la aceeasi definitie a combinarilor

C(4,2)

C(3,1)  + C(3,2)

C(2,0) +  C(2,1) C(2,1) + C(2,2)

C(1,0) + C(1,1) C(1,0) + C(1,1) 1

1 1 1

Observati cum in arborele apelurilor recursive apar apeluri in mod repetat pentru calculul aceleasi combinari. Acest efort repetat este evitat prin calcularea triunghiului lui Pascal in care fiecare combinare va fi calculata o singura data.

In mod asemanator, aceeasi diferenta de abordare va exista intre doi algoritmi de solutionare a aceleasi probleme, unul recursiv - backtracking - si altul iterativ - proiectat prin metoda programarii dinamice.

Dezavantajele acestei metode provin din faptul ca, pentru a tine minte pasii gata calculati si a evita repetarea calcularii lor (in termeni de grafuri, pentru a evita calcularea repetata a unor noduri pe ramuri diferite ale arborelui apelurilor recursive), este nevoie de punerea la dispozitie a extra-spatiului de memorare necesar si de un efort suplimentar dat de gestiunea de memorie suplimentara.

Branch & Bound.

Este strategia cea mai sofisticata de proiectare a algoritmilor. Ea a aparut datorita existentei problemelor pentru care solutia de tip backtracking poate necesita un timp astronomic de rulare a programului. In rezolvarea acestor probleme apare o asemenea penurie de informatii incit modelul abstract asociat problemei - graful de cautare a solutiilor - nu poate fi precizat in avans, din etapa de analiza. Singura solutie care ramine este includerea unui subalgoritm suplimentar ce permite construirea acestui graf pe parcurs, din aproape in aproape. Aparitia acelui subalgoritm suplimentar da numele metodei: branch&bound.

Este posibila compararea algoritmului branch&bound cu un robot ce invata sa se deplaseze singur si eficient printr-un labirint. Acel robot va fi obligat sa-si construiasca in paralel cu cautarea iesirii o harta (un graf !) a labirintului pe care va aplica apoi , pas cu pas, metode eficiente de obtinere a drumului cel mai scurt.

La strategia de cautare a solutiei in spatiul (graful) de cautare - backtracking, fiecare pas urma automat unul dupa altul pe baza unei reguli incorporate, in timp ce la strategia greedy alegerea pasului urmator era facuta pe baza celei mai bune alegeri. In cazul acestei strategii - branch&bound, pentru pasul urmator algoritmul nu mai este capabil sa faca vreo alegere pentru ca este obligat mai intii sa-si determine singur nodurile vecine ce pot fi vizitate. Numele metodei, branch=ramifica si bound=delimiteaza, provine de la cele doua actiuni ce tin locul actiunii de alegere de la strategia Greedy. Prima actiune este construirea sau determinarea prin ramificare a drumurilor de continuare, iar a doua este eliminarea continuarilor (ramurilor) ineficiente sau eronate. Prin eliminarea unor ramuri, portiuni intregi ale spatiului de cautare a solutiei raminind astfel dintr-o data delimitate si "izolate". Aceasta strategie de delimitare din mers a anumitor "regiuni" ale spatiului de cautare a solutiilor este cea care permite reducerea ordinului de marime a acestui spatiu. Solutia aceasta este eficienta doar daca cistigul oferit prin reducerea spatiului de cautare (scazind efortul suplimentar depus pentru determinarea si eliminarea din mers a continuarilor ineficiente) este substantial.

Solutiile de tip backtracking, avind la baza un schelet atit de general (algoritmul de traversare a grafului de cautare a solutiilor) sint relativ simplu de adaptat in rezolvarea unor probleme. Poate acesta este motivul care a condus pe unii programatori lipsiti de experienta la convingerea falsa ca "Orice este posibil de rezolvat prin backtracking".

La ora actuala, lista problemelor pentru care nu se cunosc decit solutii exponentiale, total nerezonabile ca durata de executie a programului de solutionare, cuprinde citeva sute de probleme, una mai celebra ca cealalta. Reamintim doar de "banala" (dar agasanta) Problema a Orarului unei institutii de invatamint care nu admite o solutie backtracking datorita duratei astronomice de asteptare a solutiei.

Datorita totalei lor ineficiente in executie, solutiile backtracking obtinute dupa o analiza si o proiectare "la prima mina" (brute-force approach, in limba engleza) ajung sa fie reanalizate din nou cu mai multa atentie. Se constata atunci ca modelul abstract asociat problemei, fie este prea sarac in informatii pentru determinarea grafului de cautare a solutiilor, fie conduce la un graf de cautare avind dimensiunea nerezonabila (exponentiala sau factoriala, fata de dimensiunea n a vectorului de intrare). Singura solutie care ramine in aceasta situatie la dispozitie este ca aceste solutii sa fie reproiectate prin metoda branch&bound.

Un exemplu usor de inteles de "problema branch&bound" il ofera Problema Generala a Labirintului. Spre deosebire de Problema Labirintului prezentata anterior (care admitea o solutie de tip backtracking), in varianta extinsa a acestei probleme, numarul directiilor posibile de urmat la fiecare pas poate fi oricit de mare, iar obstacolele pot avea orice forma si dimensiune. In acest caz, singura posibilitate este construirea "din mers" a spatiului de cautare a solutiei. Astfel, pentru determinarea unui drum de iesire din labirint sau a drumului cel mai scurt (daca este posibila determinarea acestuia in timp rezonabil!) este obligatorie adoptarea strategiei branch&bound.

Oferim in continuare o situatie concreta, ilustrata. Sesizati ca obstacolele, avind forme si dimensiuni diferite, nu pot fi ocolite decit pe un traseu "razant" sau pe un traseu ce urmeaza contorul exterior al acestora. Acest fapt complica mult problema si impune luarea unor decizii "la fata locului", in momentul intilnirii si ocolirii fiecarui obstacol, ceea ce impune o strategie de rezolvare de tip branch&bound - ramifica si delimiteaza:

Desi aceasta strategie poate sa creasca uneori surprinzator de mult eficienta algoritmilor de solutionare (din nerezonabili ca timp de executie ei pot ajunge rezonabili, datorita reducerii dimensiunii exponentiale a spatiului de cautare a solutiei), aplicarea ei este posibila doar printr-un efort suplimentar in etapa de analiza si in cea de proiectare a algoritmului. Dezavantajul major al acestei metode consta deci in efortul major depus in etapa de analiza a problemei (analiza care insa se va face o singura data si bine!) si efortul suplimentar depus in etapa proiectarii algoritmului de solutionare.

Din experienta practica este cunoscut faptul ca, pentru a analiza o problema dificila un analist poate avea nevoie de saptamini sau chiar luni de zile de analiza, in timp ce algoritmul de solutionare proiectat va dura, ca timp de executie, doar citeva zeci de minute. Daca programul obtinut nu este necesar a fi rulat decit o data, aceasta este prea putin pentru "a se amortiza" costul mare al analizei si proiectarii sale. In acea situatie, solutia branch&bound este nerentabila si, probabil ca ar fi mai ieftina strategia backtracking de solutionare, chiar si cu riscul de a obtine o executie (singura de altfel) a programului cu durata de o saptamina (ceea ce poate sa insemne totusi economie de timp).

Recursivitatea

Asa cum am amintit deja, aceasta metoda de programare poate fi privita ca forma particulara de exprimare a metodei Back-Tracking. Cu toate acestea, cei ce cunosc istoria informaticii si originile programarii stiu ca aceasta metoda are totusi un caracter special. Aceste lucruri dorim sa le evidentiem in continuare.

Inca inainte de aparitia primului calculator si, deci implicit a oricarei tehnici de programare, unii matematicieni erau profund preocupati de notiunea de calculabilitate. Aceasta notiune ii putea ajuta in efortul lor deosebit de a fundamenta notiunea elementara de algoritm sau metoda automata de calcul. In paralel, cele mai valoroase rezultate le-au obtinut latino-americanul Alonso Church si englezul Alan Turing. In timp ce Turing a introdus pentru algoritm modelul matematic abstract cunoscut sub numele de Masina Turing (care sta la bazele modelului actual de calculator), Church a fundamentat notiunea de metoda de calcul sau calculabilitatea pe functiile recursive. Astfel, teza lui Church afirma ca orice functie definita pe domeniul numerelor naturale este calculabila daca si numai daca ea este recursiva. Desi aparatul teoretic folosit de Church era in intregime matematic (se baza numai pe functii numerice naturale), lui nu i-a fost greu sa demonstreze ca orice algoritm nenumeric se reduce la functii recursive si la multimi recursive de numere naturale (pe baza unor codificari riguros alese).

Acest din urma rezultat este cel care ne intereseaza pe noi si noi il vom reformula fara ai afecta valabilitatea: orice algoritm poate fi rescris printr-un algoritm recursiv (limbajul de programare Lisp se bazeaza in intregime pe acest fapt). Chiar daca nu constituie o demonstratie riguroasa, urmatoarea echivalenta practica (descrisa in pseudo-cod) este deosebit de convingatoare: orice instructiune de ciclare este echivalenta cu un apel recursiv de subprogram sau functie.

Observam ca in cazul variantei recursive conditia de scurt-circuitare a recursivitatii este echivalenta conditiei de scurt-circuitare a ciclului. Gestiunea contorului se face in acest caz in back-ground, prin mecanismul de stiva sistem.

Putem astfel concluziona: toti algoritmii iterativi pot fi inlocuiti prin algoritmi recursivi. Avantajul celor recursivi este dat de scaderea dimensiunilor programelor si de cresterea lizibilitatii. Avantajul celor iterativi este viteza marita de executie prin gestionarea locala a parametrilor de ciclare (eliminindu-se astfel toate instructiunile push si pop pentru gestionarea stivei).

Spre edificare, va oferim in continuare citeva probleme clasice (simple) rezolvate in C prin metoda recursiva. In capitolul cu probleme ce necesita back-tracking veti gasi si alte solutii recursive (in C) ale unor probleme ceva mai dificile; astfel se vor putea sesiza mai bine avantajele acestei metode 'naturale' de programare. (Intrucit am considerat acest capitol ca fiind destul de 'tehnic', prezentam in continuare doar variantele de program in limbajul C, ce este considerat mai 'tehnic' decit limbajul Pascal.)

1. Sa se copieze un sir de caractere intr-altul.

#include <stdio.h>

char *sir1='primul',*sir2='al doilea';

void strcopy(char *sursa,char *dest)

void main(void)

2. Sa se afiseze primele n patrate perfecte.

#include <stdio.h>

#include <math.h>

int n;

void patrat(int m)

void main(void)

3.Algoritmul lui Euclid.

#include <stdio.h>

int cmmdc(int m,int n)

void main(void)

4. Se citeste n, sa se gaseasca primul numar prim mai mare decit n. (Se presupune cunoscuta demonstratia faptului ca exista p-prim mai mare decit oricare n. Sintem astfel siguri ca algoritmul se opreste! )

#include <stdio.h>

#include <math.h>

int n;

int are_divizor(int p,int d)

void prim(int p)

else prim(p+1);

void main()

5. Sa se afiseze primele n numere prime.

#include <stdio.h>

#include <math.h>

int n;

int are_divizor(int p,int d)

void prim(int p,int i)

else prim(p+1,i);

void main()

6. Se citeste n gradul unui polinom P si a[0],a[1],,a[n] coeficientii reali ai acestuia. Se citeste o valoare reala x, sa se calculeze P(x).

#include <stdio.h>

int n;

float a[20],x;

float P(int i)

void citeste_coef(int i)

void main()

7. Se citesc m si n gradele a doua polinoame P si Q, si a[0],a[1],,a[m] respectiv b[0],b[1],,b[n] coeficientii reali ai acestora. Sa se afiseze coeficientii c[0],c[1],,c[m+n] ai polinomului produs R=PxQ.

#include <stdio.h>

int m,n;

float a[20],b[20],c[40];

float suma_prod(int i,int j)

void calc_coef(int i)

void citeste_coef(float a[],int i)

void afis_coef(float a[],int i)

void main()

8. Se citeste n, o valoarea intreaga pozitiva, sa se determine suma cifrelor lui n.

#include <stdio.h>

int n;

int suma(int n)

void main()