Problema
apartenentei unui obiect la o multime de obiecte nu in mod necesar
distincte sau a incluziunii unei
secvente in alta secventa apare frecvent ca
subproblema in rezolvarea unei probleme prin metode algoritmice. Din acest
motiv algoritmii de cautare constituie o clasa speciala, masiv studiata si foarte
importanta.
Complexitatatea
Cautarea
binara foloseste ca ipoteza faptul ca multimea de
procesat este secventializata dupa o cheie de sortare
calculata in functie de compozitia obiectelor secventei sau
inclusa in structura obiectelor ca o componenta a acestora. Deci
secventa tinta este sortata. Algoritmul de cautate
binara consta in eliminarea succesiva a unei jumatati
din subsecventa aflata in curs de procesare pana cand fie elementul cautat este gasit fie
subsecventa ramasa nu mai paote fi divizata. Aceasta
eliminare a unei portiuni din subsecventa in curs de procesare este
permisa de ipoteza ordonarii care faciliteaza posibilitatea deciziei
asupra imposibilitatii aflarii elementului cautat in una
din jumatatile subsecventei. De exemplu daca cheia
elementului din mijlocul subsecventei curente este 10 si cheia
cautata este 12 iar ordonarea este crescatoare atunci sigur
elementul cautat (10) nu va fi gasit in prima jumatate.
Implementare prin liste a secevntei nu aduce un spor de eficienta algoritmului
datorita caracterului prin excelenta secvential al unei
liste care face imposibila accesarea directa a elementului aflat la
mijlocul listei. De aceea algoritmul de
cautare binara foloseste implementarea secventei sortate
sub forma de tablouri unidimesionale (vectori).
Fie
A,
de ordin n, un vector ordonat crescator. Se cere sa se
determine daca o valoare b se afla printre elementele
vectorului. Limita inferioara se numeste low, limita superioara se numeste high, iar mijlocul virtual al vectorului, mid (de la middle).

Binary_Search
(A,n,b)
return(0) //
b nu a fost gasit in tabloul A
Complexitatatea
Se observa ca, la fiecare trecere,
dimensiunea zonei cautate se injumatateste. Cazul cel mai
defavorabil este ca elementul cautat sa nu se gaseasca in
vector.
Pentru simplitate se considera n = 2k unde k
este numarul de injumatatiri. Rezulta k = log2 n si facand o
majorare, T(n) log2 n +
Deci complexitatea timp a acestui algoritm este O(log2n).
Baza logaritmului se poate ignora
deoarece: logax = logab logbx si logab este o constanta, deci ramine O(log
n), adica o functie
logaritmica.
Multimea
de obiecte in care se face cautarea poate fi organizata ca arbore
binar de cautare. Aceasta permite construirea de algoritmi de cautare eficienti.
Arborii binari de cautare sint acei arbori ale caror noduri sint organizate in
functie de valorile unor chei care sint
calculate functie de valorile nodurillor. Pentru fiecare nod, cheia sa este mai
mare decit valorile cheilor tuturor nodurilor din subarborele sting si este mai mica decit toate cheile de
noduri din subarborele drept. Nodurile arborelui au chei distincte. In figura
urmatoare este dat un arbore binar de cautare.
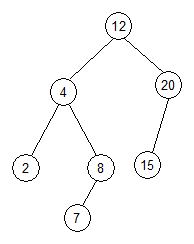
Traversarea in inordine pe un arbore binar de cautare produce o
secventa sortata crescator dupa valorile cheilor.
Operatia de creare a unui arbore binar de cautare este O(n2) timp pentru cazul cel mai defavorabil cind arborele se
construieste sub forma unei liste inlantuite. Pentru acest caz operatiile
de insertie, stergere si de cautare a unui atom se fac in O(n). Pentru
cazul mediu crearea se face in O(n * log n) iar insertia, stergerea,
cautarea se face in O(log n). O clasa speciala de arbori binari
de cautare anume arborii binari echilibrati pentru care insertia,
stergerea si cautarea se face in O(log n) pentru cazul cel mai
defavorabil.
Se considera functia de
cautare intr-un arbore binar de cautare.
search(r,x)
return(p); // return
null
unde:
r este adresa radacinii arborelui care are
noduri de forma
(data, legatura la subarborele sting, legatura la subarborele drept)
x este valoarea cimpului de date a nodului
cautat.
data(), lchild(), rchild()
sint primitivele de acces la cele trei cimpuri ale unui nod, data, legatura la subarborele sting,
legatura la subarborele drept , respectiv.
Complexitatatea
Pentru un arbore echilibrat functia lucreaza in O(logn) timp, ceea ce inseamna ca arborele binar echillibrat este
arborele binar optim atunci cind se cauta un element aleatoriu ales.
Algoritmul de
cautare naiva
Este un algoritm foarte simplu dar si foarte
ineficient: pentru fiecare pozitie posibila in sir se
testeaza daca pattern-ul se potriveste cu subsirul care
incepe cu acea pozitie.
PM_Naiv(s,n,p,m) // cauta in sirul s de dimnsiune n pattern-ul p de
dimesiune m
if (not gasit)
return
0; // pattern-ul p nu
apare in sirul s
else
return i; // pattern-ul p apare in
s pe pozitia i
Complexitatatea
Evident
complexitatea timp a algoritmului pentru cazul cel mai nefavorabil O(nm)
Algoritmul
Rabin-Karp
Algoritmul
Rabin-Karp utilizeaza tehnica tabelelor de dispersie (hashing). Un simbol
este o subsecventa de m obiecte a secventei s de dimesiune n .
Sa presupumen ca simbolurile sunt memorate intr-o tabela de
dispersie suficient de mare astfel incat sa nu existe coliziune. A testa
daca pattern-ul p coincide cu un subsir de lungime m din sirul s
este echivalent cu a testa daca valoarea functiei de dispersie h este
aceeasi pentru ambele simboluri. Pentru ca o asemenea abordare sa fie
justificata, timpul necesar evaluarii functiei h pentru un simbol din tabela de dispersie trebuie
sa fie mult mai mic decat cel necesar compararii a doua
siruri de lungime m. Aceasta se rezolva in felul urmator|:
Se
codifica fiecare sir de lungime m ca un numar intreg in baza d,
unde d este numarul maxim de obiecte din sirul s. Astfel
subsirului s[i..i+m-1] ii corespunde numarul x=index(s[i]) dm-1_+ index(s[i+1]) dm-2 + . + index(s[i+m-1]) unde index este o
functie care asociaza unui obiect din s numarul sau de
ordine intr-o secventializare a multimii obiectelor care compun s.
Functia
de dispersie H va fi definita prin h(x)=x mod q , unde q este un
numar prim suficient de mare. O deplasare la dreapta in sirul s va
corespunde inlocuirii lui x cu (x- index(s[i])dm-1) d_+ index(s[i+m])
PM-RK(s,n,p,m) // cauta in sirul s de
dimnsiune n pattern-ul p de dimesiune m
//
dm1 = (puterea m-1 a lui d modulo) q
hp=0;
for i-1..m
// hp
= valoare functiei de dispersie pentru simbolul p
hsm=0;
for i-1..m
//
hsm = valoare functiei de dispersie pentru simbolul s[1..m]
i=1;
while (hp<>hsm and i<n-m)
if (hp=hsm)
return i; // pattern-ul p apare in s pe pozitia i
else
return 0; // pattern-ul p nu apare in sirul s
Complexitatatea
Complexitatea
timp a algoritmului Rabin-Karp pentru cazul cel mai nefavorabil O(nm) dar in
practica algoritmul executa apoximativ n+m pasi.



