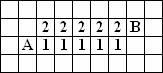
Regiuni liniare in spatiul discret
Formele subtiri, compuse din
linii drepte si curbe pot fi tratate ca regiuni foarte subtiri,
numite regiuni liniare.
Aceasta deoarece in spatiul
discret nu se poate face distinctia intre o dreapta si o
regiune. De exemplu, intre pixelii A
si B exista mai multe cai posibile: calea compusa din pixeli
egali cu1 si calea compusa din pixeli egali cu 2.
Definitie: O regiune liniara in spatiul
discret este un set de pixeli conectat cu proprietatea ca toti
pixelii sai sunt pixeli de contur.
Exemple:
Definitie: O cale simpla este o
cale in care toti pixelii sunt distincti si nici un pixel nu are
mai mult de 2 vecini-d in cale.
Definitie: Un set conectat-d este un
set in care pentru fiecare 2 pixeli A,B ai setului, exista o cale-d de la
A la B ai carei pixeli apartin setului.
Definitie: O cale-d este o cale in
care toti pixelii sunt vecini-d.
|

|
|
Vecini-d
|
Definitie: Un pixel de contur este un
pixel care are cel putin un vecin-d in afara regiunii.
Definitie: Vecinii-C ai unui pixel de contur sunt anteriorul
si succesorul sau la traversarea conturului.
|
|
|
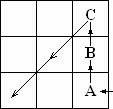
Vecinii-C ai lui B sunt A si C
|
Vecinii-C pot sa nu fie distincti. Ei sunt
distincti numai daca conturul este o cale simpla.
Definitie: Un pixel este numit pixel multiplu daca
satisface una sau mai multe dintre conditiile:
a.
Este vizitat mai mult de o data la traversarea conturului
b.
Nu are vecini in interiorul regiunii (are numai vecini-c)
c.
Are cel putin un vecin-d care apartine conturului dar care nu
este unul dintre vecinii-c ai sai
|
|
|
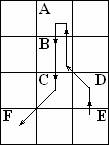
A - satisface conditia b, B -
satisface conditia a, C - satisface conditia c
|
Propozitie: O regiune liniara este o regiune
alcatuita numai din pixeli multipli. Invers, daca o regiune este
alcatuita numai din pixeli multipli, atunci ea este o regiune
liniara.
Demonstratie: O regiune liniara este
alcatuita numai din pixeli de contur, deci nici unul dintre pixelii
sai nu au vecini in interiorul regiunii, rezulta ca este
satisfacuta conditia (b) din definitia pixelilor multipli.
Extragerea regiunilor liniare din
imagini prin detectia pixelilor
multiplii
Se foloseste imaginea produsa de algoritmul de
traversare a contururilor regiunilor, in care:
pixel = 0 → pixel in afara regiunii
pixel = 1 → pixel interior
pixel = 2 → pixel de contur vizitat o singura data
pixel > 2 → pixel de contur vizitat de mai multe ori
I. Detectia
bazata pe traversarea contururilor
Pixelii multiplii sunt pixeli de contur care indeplinesc
urmatoarele conditii:
au valoarea > 2
nu au vecini cu valoarea = 1
au cel putin un vecin-d in contur care nu este vecin-c
Verificarea conditiei (3)
presupune traversarea secventiala a conturului (reprezentarea
produsa de algoritmul de traversare)
II. Detectia
bazata pe analiza vecinatatii fiecarui pixel
Detectia poate avea loc printr-o procesare secventiala sau paralela a imaginii.
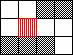
a) Pixelii care satisfac
conditia (1) sunt pixeli care conecteaza parti distincte
ale regiunilor:
|
|
Eliminand un astfel de pixel (marcat
diferit), gradul de conectivitate ale regiunii scade cu cel putin 1.
|
Astfel de pixeli pot fi recunoscuti comparand vecinatatea
fiecarui pixel cu unul dintre sabloanele urmatoare:
|
A A A
0 P 0 rotatie 90 grade
B B B
|
A 0 B
A P B
A 0 B
|
|
A A A
A P 0 rotatie 90 grade
A 0 2
|
A 0 2
A P 0
A A A
|
|
|
| rotatie 270 grade
V
rotatie
180
A A A 2 0 A
0 P A 0 P A
2 0 A A A A
|
|
| | |
Observatie: intr-un grup de pixeli marcati
cu aceeasi litera, cel putin unul are valoarea > 0.
Detectia pixelilor multipli care
satisfac unul dintre aceste sabloane poate fi efectuata procesand
direct imaginea segmentata (fara traversarea contururilor),
stiind ca pixelii de contur sunt pixeli care au cel putin un
vecin-d egal cu zero.
b) Conditia (2) poate fi
verificata foarte usor intr-un algoritm paralel: nici unul dintre
vecinii pixelului nu are valoarea 1.
c) Detectia pixelilor foloseste
imaginea segmentata dupa traversarea contururilor. Orice pixel care
satisface conditia (3) fara sa satisfaca
conditiile (1) si (2) face parte dintr-un sablon "022+" de-a
lungul unei linii orizontale sau a unei linii verticale, unde 2+
desemneaza un pixel cu valoarea ≥ 2. Pixelii de acest tip pot fi
detectati cautand sabloane de forma:
|
A A C
0 2 2+
B B C
|
C 2+ C
A 2 B
A 0 B
|
|
C B B
2+ 2 0
C A A
|
B 0 A
B 2 A
C 2+ C
|
Cel putin unul dintre pixelii
marcati cu C trebuie sa fie ≠ 0. Daca ambii sunt ≠
0, atunci A, B pot fi oricare. Daca numai unul din pixelii C este diferit
de 0 este necesar ca cel putin un A≠0 sau cel putin un
B≠0.