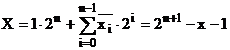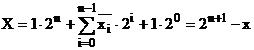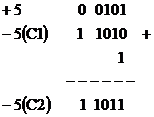Reprezentarea numerelor in virgula fixa
1.
Reprezentarea numerelor cu semn
In continuare se vor nota cu x, y
numerele in reprezentarea binara obisnuita, la care se
ataseaza semnul. Un numar cu n cifre de marime se va scrie
sub forma:
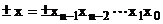
De exemplu:
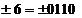
Cu  se vor nota numerele
in reprezentarea din calculator, care contin si cifrele de semn:
se vor nota numerele
in reprezentarea din calculator, care contin si cifrele de semn:

Dupa modul de
exprimare a numerelor negative, exista trei forme uzuale de reprezentare a
numerelor cu semn in virgula fixa:
In marime si semn (MS);
In complement fata de 1 (C1);
In complement fata de 2 (C2).
Pentru toate formele, un
numar pozitiv se exprima in acelasi fel:
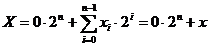 (21)
(21)
Numarul pozitiv cu semn se reprezinta deci
adaugand cifra 0 de semn in fata numarului fara semn:
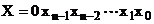
Consideram pentru simplitate numere cu 4 biti de
marime si un bit de semn. De exemplu, numarul fara
semn 5 se reprezinta prin:
iar numarul cu semn prin:
0 0101
Cea mai simpla
forma de reprezentare este cea in
marime si semn (MS).
Un numar negativ reprezentat in marime si semn are expresia:
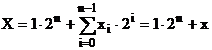 (22)
(22)
Deci, numarul negativ se reprezinta prin
adaugarea cifrei 1 de semn in fata numarului fara
semn:
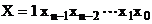
De exemplu, numarul  se va reprezenta prin:
se va reprezenta prin:
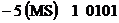
Exista mai multe dezavantaje ale acestei
reprezentari. Primul dezavantaj este ca adunarea si
scaderea necesita circuite mai complexe. Al doilea dezavantaj este
ca exista doua reprezentari pentru valoarea 0:
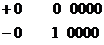
De aceea este mai dificil sa se
testeze daca o valoare este 0 (o operatie frecventa), decat in
cazul in care ar exista o singura reprezentare.
In cazul reprezentarii
in complement fata de 1,
un numar negativ se reprezinta prin complementul fata de 1
al numarului pozitiv cu aceeasi valoare absoluta. Complementul
fata de 1 al unui numar binar se obtine prin inlocuirea
bitilor de 1 cu 0, si a celor de 0 cu 1.
Un numar negativ reprezentat
in complement fata de 1 are expresia:
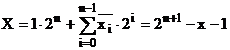 (23)
(23)
unde:  reprezinta
complementul fata de 1 al cifrei
reprezinta
complementul fata de 1 al cifrei 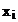 .
.
Complementul fata de 1 al
unui numar negativ se obtine prin complementarea tuturor cifrelor
numarului fara semn si adaugarea cifrei de semn 1:

De exemplu:

Exista si in acest caz
doua reprezentari pentru 0:
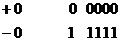
Un numar negativ
reprezentat in complement fata
de 2 are expresia:
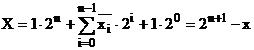 (24)
(24)
Complementul fata de 2 al
unui numar se poate obtine in mai multe moduri. O posibilitate o
reprezinta utilizarea relatiei de definitie (24). De exemplu,
considerand 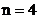 , complementul fata de 2 al numarului
, complementul fata de 2 al numarului  va fi:
va fi:
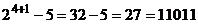
O alta
posibilitate este obtinerea complementului fata de 2 in
doua etape:
Se obtine complementul
fata de 1.
Se considera rezultatul ca un intreg fara semn, la care
se aduna valoarea
1.
De exemplu:
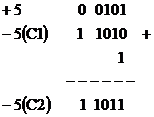
Practic, complementul fata de 2 al unui numar
se poate determina pornind de la numarul pozitiv cu semn, astfel:
Se scriu cifrele numarului incepand cu cifra c.m.p.s., neschimbate,
pana la primul 1 inclusiv.
Se complementeaza cifrele intalnite in continuare.
Exista o singura reprezentare
pentru 0 in C2. In plus, operatiile de adunare si scadere se
efectueaza cel mai simplu in aceasta reprezentare. Se poate
arata ca reprezentarea prin C2 conduce la aflarea valorii reale a
numarului, daca cifra de semn se considera negativa.
In tabelul 5 se prezinta
reprezentarea unor numere cu 4 biti de marime si un bit de semn
in MS, C1 si C2.
Tabelul 5 - Diferite moduri
de reprezentare a unor numere cu semn
In cazul reprezentarii in MS
si C1, gama numerelor care pot fi exprimate prin n biti de
marime este:
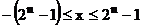 Pentru
reprezentarea in C2, aceasta gama este:
Pentru
reprezentarea in C2, aceasta gama este:
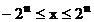
De exemplu, pentru numere de un octet
(7 cifre de marime si o cifra de semn), gama pentru reprezentarea
in MS si C1 este:
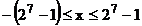
adica:
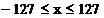
iar in C2:



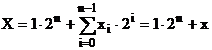 (22)
(22)