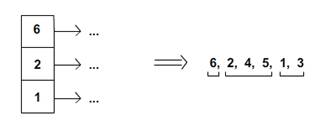SORTAREA
TOPOLOGICA
Se
da un graf orientat. Orientarea muchiilor corespunde unei relatii de
ordine de la nodul sursa catre cel destinatie. Ni se cere
sa asezam nodurile in asa fel incat pentru orice muchie
(u,v), u sa apara inaintea lui v.
Sortarea
topologica are sens numai daca este aplicata asupra unui graf
orientat si aciclic. De ce? Daca nu ar fi graf orientat, nu am avea
despre ce ordine sa discutam. Iar un ciclu ar fi indeajuns pentru a nu
putea stabili o ordine intre nodurile care il alcatuiesc.
Sa
consideram urmatorul exemplu:
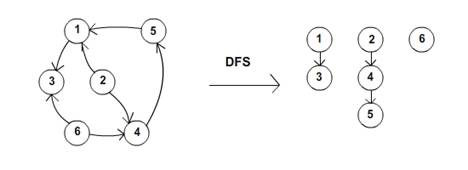
Ei bine,
de aici si pana la a obtine o succesiune de noduri ordonate nu
este decat un singur pas: avem grija sa asezam nodul
radacina al fiecarui subarbore intr-o stiva, iar
pentru afisare scoatem pe rand cate un nod din stiva tiparind
odata cu el si nodurile din arborele sau in ordinea
obtinuta.
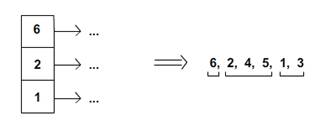
Obs: Pentru un graf dat pot exista mai multe
insiruiri de noduri care sa respecte cerinta.
O
varianta a problemei anterioare este:
O
sortare topologica a varfurilor unui graf orientat aciclic este o
operatie de ordonare liniara a varfurilor, astfel incat, daca
exista un arc ( i j ), atunci i apare inaintea lui j in aceasta ordonare.
Date de
intrare
In
fisierul de intrare sortaret.in vom avea pe prima linie
doua numere intregi N si M. Pe fiecare dintre urmatoarele M linii se vor afla
cate doua numere intregi, separate intre ele printr-un spatiu, X si Y, cu semnificatia
ca exista arc de la nodul X catre nodul Y
Date de
iesire
Fisierul
de iesire sortaret.out va contine pe o singura linie N numere separate
intre ele prin spatii, care reprezinta sortarea topologica a
nodurilor grafului dat. Daca exista mai multe solutii se va
afisa oricare.
Restrictii
1
≤ N ≤ 50000
1
≤ M ≤ 100000
Pot
exista mai multe arce intre doua noduri X si Y
Exemplu
#include
<fstream>
#include
<stack>
using
namespace std;
#define
NUME 'sortaret'
ifstream
fi(NUME'.in');
ofstream
fo(NUME'.out');
#define
MAXN 50001
int N,
M, gradin[MAXN];
int
Used[MAXN];
stack<int>
C;
struct
item *L[MAXN];
void
df(int s)
C.push(s);
inline
void add(int a, int b) ;
L[a] = p;
gradin[b] ++;
int
main()
for (int i = 1; i <= N; ++i)
if (gradin[i] == 0)
df(i);
while (!C.empty())
return 0;
Obs: Nu este singurul algoritm pentru sortare
topologica.
Optional: Un alt algoritm pentru
sortarea topologica:
Algoritmul
urmator se aplica recursiv. La fiecare pas se elimina un nod in
care nu intra nici o muchie, nod pe care il furnizam catre
output. Prin eliminare se intelege implicit ca se elimina si
muchiile adiacente nodului respectiv. Din moment ce nu erau muchii care sa
intre in el, asta inseamna ca se elimina muchiile care pornesc
din el.
Daca
la un moment dat mai avem noduri si nu mai putem face eliminare, inseamna
ca exista un ciclu in graf si nu exista sortare
topologica pentru el.