 |  |
|
Verificarea algoritmilor distribuiti
Calcul distribuit, sectiuni de calcul
(X, este o multime partial ordonata daca relatia este reflexiva, antisimetrica si tranzitiva.
O multime partial ordonata (X, este o latice daca pentru orice doua elemente exista infimum (cel mai mare minorant) si supremum(cel mai mic majorant) si cele doua elemente fac parte din multimea X.
Fie o multime X, multimea partilor lui X, notata cu P(X), impreuna cu incluziunea formeaza o latice.
Daca A, B I X, atunci sup(A,B) = A B si inf(A,B) = A B.
Dandu-se o latice, vom nota cu infimum si cu supremum. O latice este distributiva daca si numai daca
O submultime a unei latice formeaza o sublatice daca este inchisa la cele doua operatii. O sublatice a unei latice distributive este distributiva.
Fie (X, o multime partial ordonata, atunci o submultime S X se numeste ideal ordonat daca
x , y I X cu (x I S si y x) T y I S.
Multimea de idealuri ordonate a unei multimi partial ordonate X, notata cu C(X) impreuna cu incluziunea formeaza o latice distributiva.
Un element a unei latice L este join-ireductibil daca
(1) nu este cel mai mic element, si
(2) nu poate fi exprimat ca supremum(sau reuniune) a doua elemente, amandoua diferite de acesta. Formal, a L este join-ireducibil daca,
x < a, si x, y a.i. a = x y) (a = x) (a = y)
Daca X = , si L este (P(X), atunci elementele sale ireductibile la reuniune sunt , si
Daca X = , si L este (P(X), atunci elementele sale ireductibile la intersectie sunt , si
Pentru o a latice distributiva L, JI(L) desemneaza multimea elementelor sale join-ireductibile.
Multimea MI(L) a elementelor meet-ireductibile (ireductibile la intersectie sau infimum) a unei latice distributive se defineste in nod dual.
Fie L o latice distributiva finita si JI(L) multimea sa de elemente join-ireductibile.
Atunci functia f : L → C(JI(L)) definita prin:
f(a) =
este un izomorfism de la L la C(JI(L)).
In mod dual, fie P o multime partial ordonata finita. Atunci functia g : P → JI(C(P)) definita prin:
g(a) =
este un izomorfism de la P la JI(C(P)).
Teorema lui Birkho stabileste dualitatea dintre multimile partial ordonate finite si laticele distributive finite. Putem merge de la multimile partial ordonate finite la laticea distributiva finita duala construind multimea idealurilor ordonate si invers de la laticea distributiva finita la o multime partial ordonata prin selectarea elementelor join-ireductibile.
Teorema are si o varianta duala relativa la elementele meet-ireductibile.
Figura 1. (latice distributiva si reprezentarea sa prin multime partial ordonata )
Un sistem de calcul distribuit este o colectie de dispozitive de calcul individuale care comunica intre ele. Spre deosebire de procesarea paralela, in care scopul principal este cooperarea dintre toate procesoarele in vederea realizarii unei lucrari, in procesarea distribuita fiecare procesor are in general propria sa lista de sarcini independenta, dar din diferite motive (partajarea resurselor, toleranta la erori etc.) procesoarele trebuie sa-si coordoneze actiunile.
Dupa modul de comunicare si gradul de sincronizare vom considera trei modele principale:
Modelul asincron cu memorie partajata, este reprezentat de masinile puternic cuplate;
Modelul asincron cu transmitere de mesaje, este reprezentat de masinile slab cuplate si retele;
Modelul sincron cu transmitere de mesaje este o idealizare a sistemelor bazate pe transmiterea mesajelor, in care se cunoaste o anumita informatie referitoare la timp (ca de exemplu o margine superioara pentru intirzierea mesajelor).
Un sistem distribuit de tip MP consta din n procesoare: p1, p1, p2, . , pn.
Un algoritm pentru un sistem distribuit de tip MP asincron consta dintr-un program local pentru fiecare procesor din retea. Programul local permite procesarea locala (evenimente interne), precum si transmiterea si receptionarea de mesaje de la fiecare din procesele vecine in topologia data. Fecare eveniment updateaza starea procesului in cadrul caruia se executa.
Fiecare procesor pi este modelat ca o masina cu stari, cu multimea starilor finita sau infinita.
Figura 2, a) un calcul distribuit
La fiecare pas starea sistemului este data de starea fiecarui proces si de lista de evenimente care s-au petrecut de la pornirea calculului.
Fiecare proces Pi contine o stare initiala notata cu i care initializeaza procesul si o stare finala notata cu Ti.
Notam cu i stare initiala a procesului distribuit.
Notam cu T = Ti stare initiala a procesului distribuit.
Daca e este un eveniment atunci Proc(e) denota procesul pe care se executa evenimentul e. Predecesorul si succesorul unui eveniment e se noteaza prin pred(e) si respectiv succ(e).
Vom nota ordinea evenimentelor in procesul Pi prin Pi iar P este reuniunea tuturor relatiilor Pi cu 1<=i <=N.
Inchiderea reflexiva a relatiei P o notam cu →.
Modelul happened-before a lui Lamport este ce mai mica relatie tranzitiva care satisface:
daca e si f sunt in cadrul aceluiasi proces si e se produce inaintea lui f atunci e si f sunt in relatia happened-before;
daca e si f corespund unu mesaj send si unui mesaj receive atunci sunt in relatia happened-before.
Figura 2, b) laticea taieturilor consistente netriviale
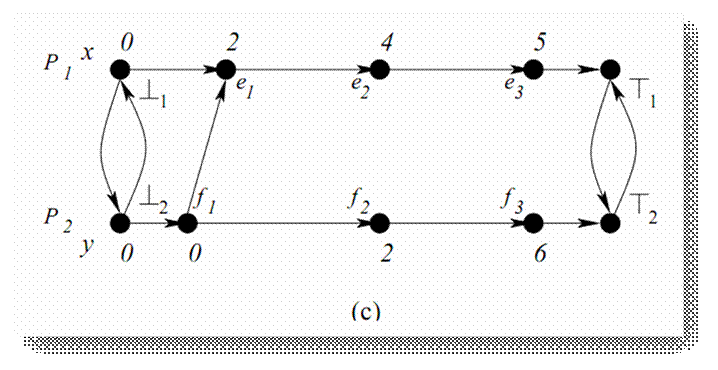
Figura 2, c) o alta reprezentare a calculului din fig. 2a
Un calcul distribuit poate fi modelat printr-un graf orientat. Vom modela un calcul distribuit (pe scurt calcul) notat prin (E, →) printr-un graf orientat avand varfurile date de o multime de evenimente E si muchiile date de multimea →.
Pentru un graf orientat G, V(G) reprezinta multimea varfurilor grafului G si E(G) reprezinta multimea muchiilor lui G. Un set de varfuri ale unui graf orientat formeaza o taietura consistenta daca si numai daca pentru orice varf din set toti vecinii de la care sosesc arce sunt si ei in set.
Altfel spus C este o taietura consistenta a lui G daca si numai daca:
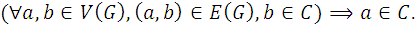
Se observa ca o taietura consistenta contine toate varfurile unui ciclu sau nu contine niciunul. Aceasta observatie poate fi generalizata la o componenta tare conexa. In mod traditional, notiunea de taietura consistenta este definita pentru multimi partial ordonate. In aceasta prezentare notiunea va fi extinsa la multimi cu o ordine arbitrara.
C(G) reprezinta multimea tuturor taieturilor consistente ale unui graf orientat. Multimea vida si V(G) apartin lui C(G) si se numesc taieturi consistente triviale.
Presupunem ca toate evenimentele initiale apartin aceleiasi componente tari conexe. Aceasta presupunere ne asigura ca orice taietura consistenta netriviala va contine toate evenimentele initiale si niciun eveniment final. Ca o consecinta, orice taietura consistenta a unui calcul in modelul traditional este netriviala in acest model si invers. In acest model se pot trata si sectiunile vide intr-o maniera convenabila. In acest model un calcul distribuit poate contine cicluri deoarece un calcul in modelul traditional surprinde ordinea observabila a executarii evenimentelor, in timp ce in noul model sunt surprinse taieturile consistente.
Taietura consistenta initiala Ř si cea finala E din modelul traditional corespund lui si e = E- din noul model.
Notiunea de taietura consistenta este similara notiunii de ideal ordonat. Rezulta ca ( C(G), ) formeaza o latice distributiva.
Teorema rezulta din faptul ca reuniunea si intersectia a doua taieturi consistente reprezinta tot doua taieturi consistente.
Doua grafuri G si H sunt echivalente daca C(G) = C(H).
Notam cu P(G) multimea tuturor perechilor(u,v) astfel incat exista un drum de la u la v in G. Consideram ca fiecare varf are un drum catre el insusi.
Doua grafuri G si H sunt path-echivalente daca pentru orice cale de la u la v in G exista o cale de la u la v in H si invers P(G) = P(H).
Daca G si H sunt
doua grafuri orientate pe acelasi set de varfuri atunci P(G) P(H) 
C(G) C(H).
Adica doua grafuri orientate sunt cut-echivalente daca si numai daca sunt path-echivalente. Acest lucru este foarte important deoarece path-echivalenta poate fi verificata intr-un timp polinomial (|P(G)|=O(|V(G)|2)), iar cut-echivalenta este mult mai greu de verificat, avand o complexitate de |C(G)|=O(2|V(G)|).
O frontiera a unei taieturi consistente este data de un set de evenimente ale taieturii ale caror succesori, daca exista, nu sunt cuprinsi in taietura.
Frontier(C):=.
O taietura consistenta este caracterizata in mod unic de frontiera sa si reciproc.
Spunem ca doua evenimente sunt consistente daca si numai daca sunt continute in frontiera unei taieturi consistente, altfel ele sunt inconsistente.
In figura urmatoare se poate observa un calcul si laticea taieturilor consistente netriviale. O taietura consistenta este reprezentata in figura prin frontiera sa. De pilda taietura consistenta D este reprezentata de .
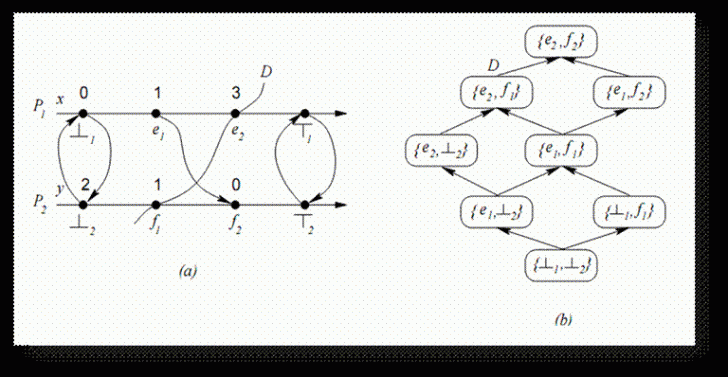
Figura 3 - Un calcul distribuit si laticea corespunzatoare taieturilor sale
In aceasta sectiune, definim notiunea de sectiune a unui calcul referitoare la un predicat. Definitia data aici este mai slaba decat definitia in lucrarea [6]. Cu toate acestea, sectiunea exista acum pentru orice predicat ( nu doar pentru predicate specifice ).
(Sectiunea): O sectiune a unui calcul relativa la un predicat este cel mai mic graf orientat - cu numarul minim de taieturi consistente - care contine toate taieturile consistente care satisfac predicatul, ale calculului original.
O sectiune dintr-un graf relativa la un predicat este un graf orientat otinut din G prin adaugarea muchiilor astfel incat:
(1) contine toate taieturile consistente care satisfac predicatul si
(2) dintre toate grafurile care satisfac (1), contine cel mai mic numar de taieturi consistente.
Vom arata mai tarziu ca cel mai mic calcul este bine definit pentru fiecare predicat. O sectiune de calcul (E, →) referitoare la predicatul b este indicat de (E, →)b. Sa notam ca (E, →) = (E, →)true
In continuare vom folosi cu acelasi sens termenii de "calcul" si "sectiune".
In modelul nostru, fiecare sectiune derivata din calculul (E, →) va avea sectiunile consistente triviale Ř si E in setul ei de taieturi consistente. Prin urmare, o sectiune este vida daca si numai daca nu are taieturi consistente non-triviale.
O sectiune de calcul cu privire la un predicat este slab daca si numai daca fiecare taietura consistenta a sectiunii satisface predicatul.
Figura 4: (a) Sublaticea unei latice din figura 3(b) relativa la predicatul ((x<2) ^ (y>1))V (x<1) si (b) sectiunea corespunzatoare.
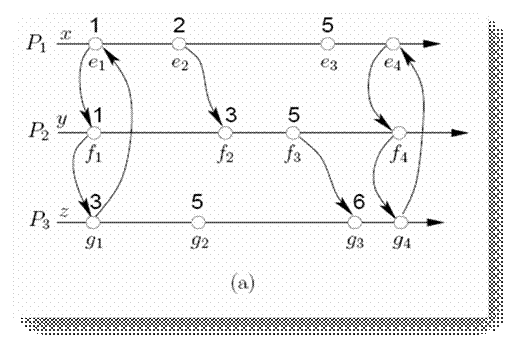
Figura 5, a) un calcul
Legenda
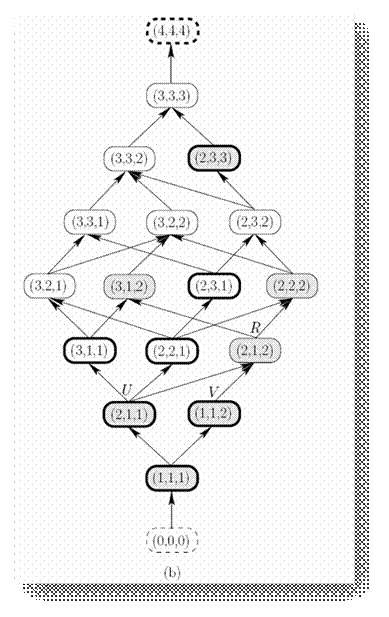
Figura 5, b) laticea taieturilor consistente
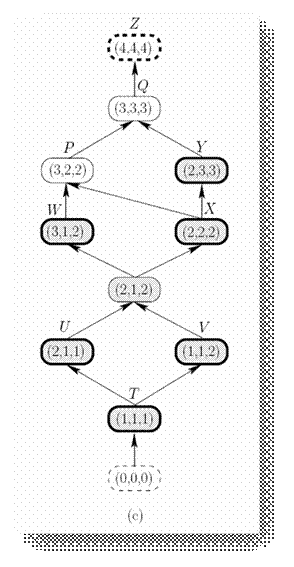
Figura 5, c) cea mai mica sublatice care contine toate taieturile consistente
care satisfac predicatul x + y − z ≤ 1,
Figura 5, d) multimea partial ordonata indusa de elementele join-ireductibile ale sublaticei 5.b
Un predicat global este regular daca si numai daca multimea taieturilor consistente care satisfac predicatul formeaza o sublatice a laticei taieturilor consistente.
In mod echivalent, daca doua taieturi consistente satisfac un predicat regular atunci taieturile date de intersectia si de reuninunea lor vor satisface predicatul.
Cateva exemple de predicate regulare sunt orice predicate regulare si predicate de canal cum ar fi " sunt cel mult k mesaje in tranzitul de la Pi la Pj".
Clasa de predicate regulare este inchisa la conjunctie. Este dovedit faptul ca sectiunea unui calcul relativ la un predicat este slaba daca si numai daca predicatul este regular.
Vom prezenta algoritmul de generare a unei sectiuni.
Fiind data o sublatice L' si un varf e, notam cu JL'(e) cea mai mica taietura consistent din L care apartine lui L' si care contine e.
Daca nu exista o astfel de taietura atunci JL'(e) = E (taietura triviala).
Daca e = T atunci JL'(e) = E.
Daca e = atunci JL'(e) = cel mai mic element a lui L'
Daca L este o latice distributiva generata de un graf G, atunci orice sublatice a lui L poate fi generata de un graf G' obtinut din G prin adaugarea de muchii.
JL'(e) corespunde elementelor join-ireductibile ale sublaticei L'. Rezulta (T. Birkhoff ) ca obtinem G' calculand multime partial ordonata indusa de JL'(e).
Pentru orice graf orientat G si pentru orice predicat p, slice(G,p) exista si este unic
Consideram laticea de taieturi consistente din Figura 5 (b).
Taieturile consistente care satisfac predicatul x + y − z ≤ 1 sunt hasurate in figura. Figura 5 (c) caontinece mica sublatice care contine aceste taieturi.
Taieturile consistente P si Q nu satisfac predicatul dar au fost incluse pentru a completa sublaticea. Elementele join-ireducibile din sublatice sunt desenate cu o margine ingrosata. Sunt in total sapte elemente; T, U, V , W, X, Y si Z.
Figure 5(d) contine multimea partial ordonata indusa de multimea J = .
Exista o corespondenta unu la unu dintre elemental join-ireductibile si multimea de component tari conexe din graful din Figure 5(d).
Se poate verifica orice taietura consistent din sublatice se poate exprima ca o reuniune a submultimilor din J si
Reuniunea oricarei submultimi din j este o taietura consistent a sublaticei.
In continuare aratam cum sectionarea poate fi folosita pentru a monitoriza predicatele in sisteme distribuite.
Un predicat poate fi monitorizat prin patru modalitati, si anume posibil, cu siguranta, invariant si controlabil. Un predicat este posibil adevarat intr-un calcul daca si numai daca exista o taietura consistenta a calculului care satisface predicatul. Pe de alta parte, un predicat cu siguranta este valid intr-un calcul daca si numai daca eventual devine adevarat in toate executarile calcului ( run este un drum in laticea taieturilor consistente).
Predicatele invariante : b si controlabile : b sunt duale ale predicatelor posibile : b si respectiv cu siguranta : b.
Detectarea predicatelor implica in mod normal detectarea predicatelor prin modalitatea posibil in timp ce controlul predicatelor implica monitorizarea unui preidcat cu modalitatea controlabil. Monitorizarea are aplicatii in ariile de testare si corectarea si toleranta greselilor software a programelor distribuite.
Urmatoarea teorema descrie cum posibil : b, invariant : b si controlabil : b pot fi calculate folosind notiunea de sectiune cand b este un predicat regular. Nu cunoastem inca complexitatea calcularii cu siguranta : b cand b este regular. Avem graful orientat G, fie scc(G) numarul de componente tari conexe ale lui G.
Teorema Un predicat regular este
posibil adevarat intr-un calcul daca si numai daca sectiunea calculului relativ la predicat are cel putin o taietura non-triviala consistenta, adica, are cel putin doua componente tari conexe. Formal,
posibil:b:= scc((E, →)b) >= 2
invariant intr-un calcul daca si numai daca sectiunea calculului cu privire la predicat este cut-echivalent cu calculul. Formal,
invariant:b := (E, →)b
(E, →)
controlabil intr-un calcul daca si numai daca sectiunea calculului cu privire la predicat are acelasi numar de componente tari conexe ca si calculul. Formal,
conrolabila:b := scc( (E, →)b) =scc( (E, →))
Demonstratie : Primele doua posibilitati sunt evidente. In ceea ce priveste ultima propozitie, se poate verifica faptul ca un predicat regular este controlabil intr-un calcul daca si numai daca exista un drum de la taietura consistenta initiala pana la cea finala in latice, generat de multimea de taieturi consistente ale calculului, astfel incat fiecare taietura consistenta aflata de-a lungul drumului satisface predicatul. Aceasta se intampla numai atunci cand lungimea celui mai lung lant in sublatice, cuprins de multimea de taieturi consistente care satisfac predicatul, este egal cu cel mai lung lant in latice, ce corespunde multimii tuturor taieturilor consistente. Pentru o latice distributiva finita, lungimea celui mai lung lant al ei este egala cu cu numarul sau de elemente ireductibile (la reuniune). Mai mult, pentru un graf orientat, numarul de elemente ireductibile ale laticei generate de multimea sa de taieturi consistente--atat triviale cat si non-triviale-este acelasi ca si numarul sau de componente tari conexe. Aceasta se intampla pentru ca, din teorema de reprezentare a lui Brikhoff pentru latice finite distributive graful de componente ce corespunde unui graf orientat (care este un graf cu varfuri precum componentele tari conexe ale grafului orientat dat) este izomorf pe multimea de elemente ireductible ale laticei generate de taieturile consistente al grafului orientat.
Observati faptul ca prima propozitie este valida pentru orice predicat arbitrar. Dat fiind faptul ca detectarea validitatii unui predicat intr-un calcul este NP-completa in general, tot NP-completa este si determinarea daca pentru un predicat exista o sectiune non-vida.
In aceast paragraf, aratam ca acea sectiune exista si este bine definita in ceea ce priveste fiecare predicat. Stim ca acest lucru este adevarat cel putin pentru predicatele regulare. In plus, sectiunea referitoare la un predicat regular e slaba. Exploatam aceste fapte si definim un operator de incheiere, indicat prin reg, care, dat fiind un calcul, converteste predicatul arbitrar intr-un predicat regular satisfacand anumite proprietati. Dat fiind un calcul (E, →) , fie R(E) ce indica multimea de predicate care sunt regulare si se refera la calcul (→ este implicit).
Dat fiind predicatul b, definim reg(b) ca fiind predicatul care satisface urmatoarele conditii:
este regular, adica reg(b)I R(E)
este mai slab decat b, adica b T reg(b)
este mai puternic decat orice alt predicat care satisface (1) si (2), adica
b'IR(E) cu bT b' atunci reg(b) T b')
Cu alte cuvinte, reg(b) este cel mai puternic predicat mai slab decat b. In general, reg(b) nu depinde numai de predicatul b ci si de calculul luat in considerare. Presupunem dependenta fata de calcul ca fiind implicita si o explicitam numai cand este necesar. Urmatoarea teorema stabileste faptul ca reg(b) exista pentru orice predicat b. Observam ca sectiunea pentru b este data de sectiunea pentru reg(b). Astfel, sectiunea exista si este bine definita pentru toate predicatele.
Dat fiind predicatul b, reg(b) exista si este bine definit.
Demonstratie: Fie Rb(E) multimea preidcatelor regulare in R(E) mai slabe decat b. Observam ca Rb(E) este nevida deoarece true este un predicat regular mai slab decat b si deci continut de Rb(E). Introducem reg(b) ca fiind conjugarea tuturor predicatelor in Rb(E). Formal,
Ramane sa aratam ca reg(b) astfel definit satisface intradevar cele trei conditii cerute. Conditia (1) este indeplinita deoarece clasa de predicate regulare este inchisa la conjugare. Conditia (2) este indeplinita deoarece fiecare predicat in Rb(E) este mai slab decat b si deci conjugarea lor este mai slaba decat b. In final, fie b' un predicat ce satisface conditiile (1) si (2). Notam ca b'IRb(E). Deoarece conjugarea predicatelor este mai puternica decat orice parte a conjugarii, reg(b) este mai puternic decat b'. Astfel reg(b) satisface conditia (3).
Astfel, dat fiind calculul (E, →) si un predicat b, sectiunea lui (E, →) cu privire la b poate fi obtinuta prin aplicarea mai intai a operatorului reg lui b pentru a obtine reg(b) si apoi calculand sectiunea lui (E, →) cu privire la reg(b). In mod echivalent,
(E, →)b = (E, →)reg(b)
Teorema reg este un operator de inchidere. Formal,
reg(b) este mai slab decat b, adica, adica b T reg(b)
reg este monoton, adica, daca b T b' atunci reg(b) T reg(b')
reg este idempotent, adica, reg(reg(b)) = reg(b).
Demonstratie:
reg(b) este mai slab decat b reiese din definitie.
reg este monoton.
Deoarece reg(b') este mai slab decat b', este mai slab decat b. Mai precis, reg(b') este un predicat regular mai slab decat b. Prin definitie, reg(b) este cel mai puternic predicat regular mai slab decat b. Astfel reg(b) este mai puternic decat reg(b') sau, cu alte cuvnite, reg(b) T reg(b').
reg este idempotent.
Reiese din faptul ca reg(b) este un predicat regular si este mai slab decat reg(b).
(R, T formeaza o latice.
Operatiile pe laticea R sunt definite astfel: fie doua predicate regulare b1 si b2 avem operatiile:
Notiunea duala a lui reg(b), cel mai slab predicat regular mai puternic decat b, este imaginabil. In orice caz, urmatorul exemplu dovedeste ca un astfel de predicat nu poate fi bine definit.
N. Mittal and VK Garg.
Computation Slicing: Techniques and Theory. Technical Report, The Parallel and
Distributed Systems Laboratory, Department of Electrical and Computer
Engineering, The
Attiya, H., Welch, J.:
Distributed Computing: Fundamentals, Simulations and Advanced Topics. 2nd ed.
Wiley,
Chase and V. K. Garg. Detection of Global Predicates: Techniques and their Limitations. Distributed Computing, 11(4):191-201, 1998
V. K. Garg and N.
Mittal. On Slicing a Distributed Computation. In Proceedings of the 21st
IEEE International Conference on Distributed Computing Systems (ICDCS), pages
322-329,
L. Lamport. Time, Clocks, and the Ordering of Events in a Distributed System. Communications of the ACM (CACM), 21(7):558-565, July 1978.
Lynch, N.: Distributed Algorithms. Morgan Kaufmann, (1996)
N. Mittal and V. K.
Garg. Debugging Distributed Programs Using Controlled Re-execution. In Proceedings
of the 19th ACM Symposium on Principles of Distributed Computing (PODC), pages
239-248,
B. Finkbeiner and H. B. Sipma. Checking Finite Traces using Alternating Automata. In Proceedings of the 1st International Workshop Run-time Verification (RV), volume 55 of Electronic Notes in Theoretical Computer Science. Elsevier Science Publishers B. V. (North-Holland), 2001.
Korel and R. Ferguson. Dynamic Slicing of Distributed Programs. Applied Mathematics and Computer Science Journal, 2(2):199-215, 1992.
Acest document nu se poate descarca
| E posibil sa te intereseze alte documente despre:
|
| Copyright © 2024 - Toate drepturile rezervate QReferat.com | Folositi documentele afisate ca sursa de inspiratie. Va recomandam sa nu copiati textul, ci sa compuneti propriul document pe baza informatiilor de pe site. { Home } { Contact } { Termeni si conditii } |
Documente similare:
|
Cauta document |