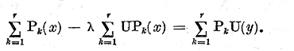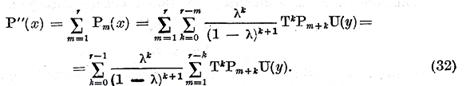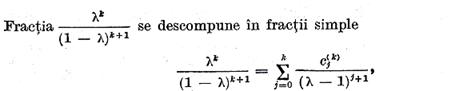Comportarea rezolventei in vecinatatea valorilor caracteristice
Daca U
este un operator compact , atunci rezultatelor teoremelor III.3.1 si III.3.4.
li se adauga fapte mai fine , relative la comportarea rezolventei in
vecinatatea unei valori caracteristice.
Un operator liniar continuu V va fi numit
finit-dimensional daca el
aplica spatiului X intr-un subspatiu finit-dimensional 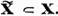 Sa alegem in
Sa alegem in  un sistem complet de elemente liniar
independente
un sistem complet de elemente liniar
independente  Prin definitie , pentru
Prin definitie , pentru 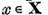 arbitrar
arbitrar
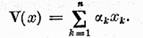
Coeficientii 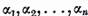 depind evident de x. Punand
depind evident de x. Punand
 ne convingem ca
functionalele
ne convingem ca
functionalele  sunt liniare si continue.: liniaritatea
nu ridica nici un dubiu iar continuitatea rezulta din faptul ca
daca un sir de elemente ale unui spatiu normat finit-dimensional
converge catre zero atunci si fiecare coordonata tinde
catre zero.
sunt liniare si continue.: liniaritatea
nu ridica nici un dubiu iar continuitatea rezulta din faptul ca
daca un sir de elemente ale unui spatiu normat finit-dimensional
converge catre zero atunci si fiecare coordonata tinde
catre zero.
Obtinem astfel
 (18)
(18)
Reciproc orice operator V reprezentabil sub forma
(18) va fi desigur finit-dimensional.
Sa remarcam ca un operator
finit-dimensional este in mod necesar compact.
Sa consideram acum un operator compact U
si fie 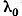 o valoare caracteristica a sa. Este
variabila :
o valoare caracteristica a sa. Este
variabila :
Teorema III.5.1. Operatorul U poate fi reprezentat sub forma

unde
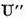 este un operator finit-dimensional,
este un operator finit-dimensional,  este compact iar multimea
caracteristica a operatorului
este compact iar multimea
caracteristica a operatorului 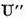 se compune doar din punctul
se compune doar din punctul  pe cand multime caracteristica a
lui
pe cand multime caracteristica a
lui se obtine
prin inlaturarea punctului
se obtine
prin inlaturarea punctului  din multimea caracteristica a lui U.
din multimea caracteristica a lui U.
Demonstratie: Se poate considera  = 1(in caz contrar am
considera in locul lui U operatorul
= 1(in caz contrar am
considera in locul lui U operatorul 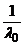 U).In aceasta ipoteza,vom demonstra ca descompunerea
operatorului U in suma
U).In aceasta ipoteza,vom demonstra ca descompunerea
operatorului U in suma  indicata in teorema I.2.1.
indeplineste conditiile date.
indicata in teorema I.2.1.
indeplineste conditiile date.
Vom
folosi notatiile din teorema I.2.1. Sa verificam ca operatorul
 are unica valoare caracteristica
are unica valoare caracteristica 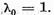
Intradevar daca 
 si prin urmare , pe baza definitiei
operatorului
si prin urmare , pe baza definitiei
operatorului 

si  este valoarea caracteristica a
operatorului
este valoarea caracteristica a
operatorului 
Daca

pentru un  atunci deoarece
atunci deoarece  vom avea
vom avea 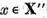 si prin urmare
si prin urmare  astfel ca
astfel ca  dar
dar 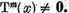
In virtutea egalitatii (19)
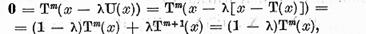
ceea ce este posibil doar pentru 
Astfel unica valoare caracteristica a
operatorului 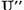 este
este 

Sa demonstram acum afirmatia
teorema asupra multimii caracteristice operatorului 
Deoarece conform teoremei I.2.1. operatorul  are invers
are invers 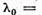 1 nu este valoarea caracteristica a
operatorului
1 nu este valoarea caracteristica a
operatorului  Fie
Fie  o valoare
catacteristica a operatorului U
si
o valoare
catacteristica a operatorului U
si  un vector propriu
corespunzator . Daca cumva
un vector propriu
corespunzator . Daca cumva  atunci rationand ca si mai sus, am
obtine
atunci rationand ca si mai sus, am
obtine 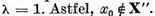
De aceea in descompunerea
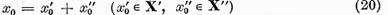
trebuie sa avem 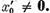 In virtutea unicitatii
descompunerii (20) din relatia
In virtutea unicitatii
descompunerii (20) din relatia

obtinem 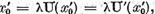 adica
adica  este valoarea
caracteristica a operatorului
este valoarea
caracteristica a operatorului 
Invers , fie  o valoare caracteristica operatorului
o valoare caracteristica operatorului  si
si 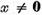 este un vector propriu asociat . Deoarece
este un vector propriu asociat . Deoarece

avem  adica
adica 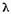 este valoarea caracteristica a
operatorului U.
este valoarea caracteristica a
operatorului U.
Celelalte afirmatii ale teoremei sunt
continute in teorema I.2.1.
Teorema este astfel demonstrata.
O imagine mai completa a comportarii
rezolventei in vecinatatea unei valori caracteristice se poate obtine
pe baza urmatoarei teoreme.
Teorema III.5.2. Fie  o valoare caracteristica a operatorului
U. Atunci intr-o vecinatate suficient de mica a punctului
o valoare caracteristica a operatorului
U. Atunci intr-o vecinatate suficient de mica a punctului  are loc dezvoltarea
are loc dezvoltarea

aici
r este rangul valorii caracteristice  ; iar
operatorii
; iar
operatorii  sunt finit-dimensionali; operatorul
sunt finit-dimensionali; operatorul 
Seria
din numarul drept al relatiei (21) converge in spatiul de
operatori B(X, X)
Demonstratie. Ca si in demonstratia teoremei
precedente, vom considera  Sa remarcam de la inceput ca ,
pe baza lemei I.1.2. rangul valorii caracteristice
Sa remarcam de la inceput ca ,
pe baza lemei I.1.2. rangul valorii caracteristice  este finit. Folosind notatiile teoremei
I.2.1. pe baza observatiei la aceasta teorema , vom observa
ca
este finit. Folosind notatiile teoremei
I.2.1. pe baza observatiei la aceasta teorema , vom observa
ca 
Reprezentand elementul  sub forma
sub forma

si asociind elementul x elementului 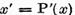 si elementul
si elementul vom construi
operatorii
vom construi
operatorii 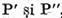 , proiectorii spatiului
X pe subspatiile
, proiectorii spatiului
X pe subspatiile  In virtutea aceastei estimari (9) din
cap. I, acesti operatori sunt continui. Sa remarcam ca
In virtutea aceastei estimari (9) din
cap. I, acesti operatori sunt continui. Sa remarcam ca
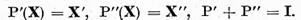
Sa consideram un element arbitrar 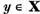 . Elementul
. Elementul  este solutia ecuatiei
este solutia ecuatiei

Inlocuind aici  si tinand cont ca
si tinand cont ca 
 putem pune ecuatia (22) sub forma unui
sistem de doua ecuatii
putem pune ecuatia (22) sub forma unui
sistem de doua ecuatii

Observand ca 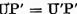 , prima
ecuatie se poate scrie sub forma
, prima
ecuatie se poate scrie sub forma

unde am notat,  . In virtutea
teoremei I.4.1,
. In virtutea
teoremei I.4.1,  este valoare regulata a operatorului
este valoare regulata a operatorului  .Daca
.Daca  este suficient de mic, rezolvanta
este suficient de mic, rezolvanta  admite dezvoltarea
admite dezvoltarea

unde seria din membrul drept converge in
spatiul  . Astfel putem
scrie
. Astfel putem
scrie

unde  si seria din membrul drept converge ca
si mai inainte in spatiul
si seria din membrul drept converge ca
si mai inainte in spatiul  .
.
Sa ne ocupam acum de a doua ecuatie
(23)
Sa formam spatiul cat

si sa notam  omomorfismul natural al spatiului
omomorfismul natural al spatiului  . Spatiul
. Spatiul 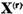 este evident
finit-dimensional. Sa alegem in el un sistem complet de elemente liniar
independente
este evident
finit-dimensional. Sa alegem in el un sistem complet de elemente liniar
independente 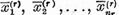 si fie
si fie 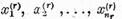 elemente ale lui
elemente ale lui 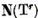 astfel incat
astfel incat 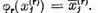 Elementele
Elementele  fac parte
din
fac parte
din  . Pe langa
aceasta imaginile lor
. Pe langa
aceasta imaginile lor  sunt liniar independente deoarece daca
sunt liniar independente deoarece daca

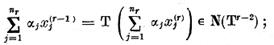
altfel spus,
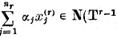
si prin urmare

ceea ce este posibil doar pentru 
Sa competam sistemul de elemente  cu elemente
cu elemente  astfel ca sa obtinem o baza in
astfel ca sa obtinem o baza in 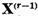 . Sa alegem
apoi
. Sa alegem
apoi  astfel ca
astfel ca 
Continuand sa rationam in acest fel
construim pentru fiecare 
 elementele
elementele 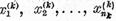 astfel ca
astfel ca
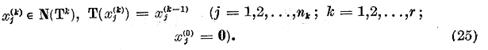
In plus elementele

formeaza pentru fiecare  baza in spatiul
baza in spatiul 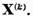
Sa notam

Ca urmare a relatiilor (25)
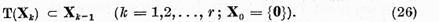
Vom demonstra acum ca elementele : 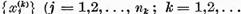
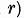
formeaza un sistem complet de
elemente liniar independente in 
Fie
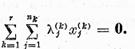
Deoarece 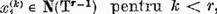 prin aplicarea operatorului
prin aplicarea operatorului  obtinem
obtinem

si prin urmare  Ne convingem analog ca si
ceilalti coeficienti
Ne convingem analog ca si
ceilalti coeficienti 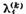 sunt egali cu zero. Sa consideram
acum un element arbitrar
sunt egali cu zero. Sa consideram
acum un element arbitrar  Elementul
Elementul  si de aceea exista coeficientii
si de aceea exista coeficientii

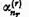 astfel incat
astfel incat

De aceea

Continuand prin aceste rationamente asemanatoare obtinem in cele din urma ca exista  astfel incat
astfel incat
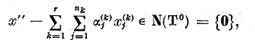
si prin urmare

Fie x un element arbitrar din
X . Elementul  , de unde
, de unde

si dupa cum s-a observat in sectiunea III.5.
coeficientii 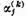 sunt functionale liniare. Daca
notam
sunt functionale liniare. Daca
notam
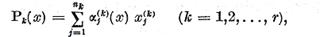
atunci pe baza celor spuse  va fi operator continuu din X pe
va fi operator continuu din X pe  iar
iar

Luand in considerare relatia 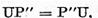 vom scrie membrul drept al celei de a doua
ecuatii (23) sub forma
vom scrie membrul drept al celei de a doua
ecuatii (23) sub forma  dupa care vom inlocui operatorul
dupa care vom inlocui operatorul 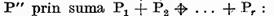
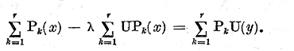
Aplicand ambilor membri ai acestei egalitati operatorul 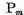 , tinand cont de
(28) obtinem
, tinand cont de
(28) obtinem
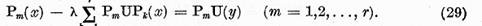
dar

de aceea ca urmare a incluziunii (26)

Folosind aceasta relatie putem scrie ecuatia (29) intr-o
forma mai simpla
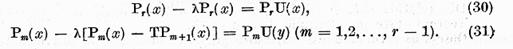
Din (30) gasim
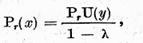
si prin urmare , pe baza ecuatiei (31)

si in general pentru orice 

Din egalitatile obtinute deducem
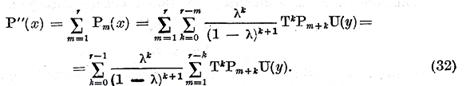
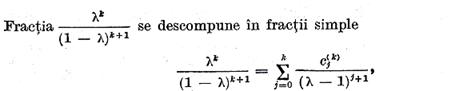
unde 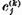 sunt constante si
sunt constante si  Introducand aceasta in (32) obtinem
Introducand aceasta in (32) obtinem

unde operatorii  sunt combinatii
liniare de operatori de forma
sunt combinatii
liniare de operatori de forma 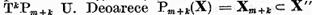 si pe baza punctului b) din teorema I.2.1.
si pe baza punctului b) din teorema I.2.1.
 rezulta
ca operatorii
rezulta
ca operatorii
 aplica spatiul X in
aplica spatiul X in  si prin
urmare , sunt finir dimensionali. Apoi din egalitatea (32) se vede ca
si prin
urmare , sunt finir dimensionali. Apoi din egalitatea (32) se vede ca

De aceea daca de exemplu 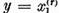 atunci din relatiile (25)
atunci din relatiile (25)

astfel incat 
Din relatiile (24) si (33) obtinem dezvoltarea dorita a rezolventei  . Teorema este in intregime demonstrata.
. Teorema este in intregime demonstrata.
Observatie. Daca U este operator
autoadjunct intr-un spatiu Hilbert,
teorema poate fi intrucatva precizata , deoarece in acest caz r = 1 si prin urmare , in dezvoltarea
(21) va aparea doar un singur termen cu exponent negativ al lui  anume
anume 



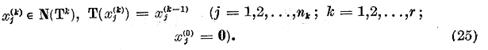
 baza in spatiul
baza in spatiul