Elemente
de teoria  - semigrupurilor de operatori
- semigrupurilor de operatori
Fie X un
spatiu Banach real sau complex. In tot ceea ce urmeaza, notam cu
B(X) algebra Banach a
operatorilor liniari si marginiti pe X .
Consideram de asemenea problema Cauchy abstracta
(A)  ,
,
unde 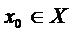 , iar A este generatorul infinitezimal
al unui semigrup de clasa
, iar A este generatorul infinitezimal
al unui semigrup de clasa 
Definitia I.1.1. O familie S 
 B(X) se zice semigrup de operatori daca
indeplineste urmatoarele conditii:
B(X) se zice semigrup de operatori daca
indeplineste urmatoarele conditii:
(i) S(0) = I ;
(ii) S(t+
s) = S(t) S(s), pentru orice t , s  0.
0.
Daca
in plus, are loc
(iii) 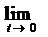 S(t)x = x, pentru
orice x
S(t)x = x, pentru
orice x 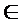 X
X
atunci S = 
 se zice de clasa
se zice de clasa
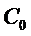 sau
sau 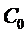 - semigrup.
- semigrup.
Fie S  un
un 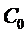 - semigrup
pe X . Consideram
multimea
- semigrup
pe X . Consideram
multimea
D(A)
: = .
Definitia I.1.2. Operatorul
A : D(A) X, Ax : =
X, Ax : =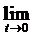

se
numeste generatorul infinitezimal
al 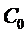 - semigrupului
- semigrupului
S =  .
.
Exemplul I.1.1. Fie A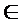 B(X) si pentru fiecare t
B(X) si pentru fiecare t 0, fie
0, fie
S(t) : X X, S(t)x
: =
X, S(t)x
: =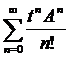 x.
x.
Uzual S(t)
se noteaza cu
si X 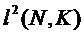 : =
: = este un
este un 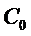 - semigrup, atunci
exista doua constante M
- semigrup, atunci
exista doua constante M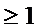 si
si  astfel incat
astfel incat
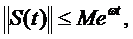
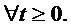
Teorema I.1.2. ( Proprietati ale 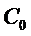 - semigrupurilor )
- semigrupurilor )
Fie S =  un
un
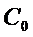 - semigrup, iar A generatorul sau infinitezimal.
Atunci, au loc urmatoarele proprietati:
- semigrup, iar A generatorul sau infinitezimal.
Atunci, au loc urmatoarele proprietati:
(i)
pentru orice 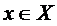 , aplicatia
, aplicatia  este continua pe R
este continua pe R ;
;
(ii)
daca x D(A), atunci S(t)x
D(A), atunci S(t)x  , pentru orice t >
0 si
, pentru orice t >
0 si
AS(t)x=S(t)Ax;
(iii ) daca x 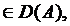 atunci aplicatia t
atunci aplicatia t S(t)x : (0,
S(t)x : (0, este derivabila si
este derivabila si

(iv) daca
x 
S(t)x
- S(s)x=  ,
, 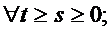
(v) 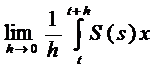 ds=S(t)x, pentru orice
x
ds=S(t)x, pentru orice
x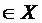 si orice t
si orice t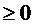 ;
;
(vi) pentru orice x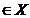 si penru orice t > 0,
si penru orice t > 0, 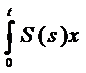 ds
ds  D(A)
si A (
D(A)
si A (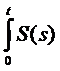 x ds)=S(t)x -x;
x ds)=S(t)x -x;
(vii) 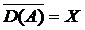 , adica domeniul generatorului este dens in X;
, adica domeniul generatorului este dens in X;
(viii) A este un operator liniar inchis.
Definitia I.1.3. O familie U=
 se zice
se zice 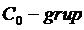 daca
indeplineste urmatoarele conditii :
daca
indeplineste urmatoarele conditii :
(i) U(0) = I , identitatea pe spatiul X;
(ii) U(t+s)= U(t)U(s),
pentru orice t, s  ;
;
(iii) 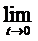 U(t)x=x , pentru orice x
U(t)x=x , pentru orice x 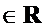 ;
;
Teorema I.1.4. FieS = un C
un C - semigrup. Urmatoarele afirmatii sunt echivalente:
- semigrup. Urmatoarele afirmatii sunt echivalente:
(i) S poate fi extins la un C - grup;
- grup;
(ii) exista t astfel incat S(t
astfel incat S(t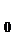 ) este inversabil;
) este inversabil;
(iii)
pentru orice t > 0, S(t) este inversabil.
Definitia I.2.1. Semigrupul S=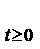 se zice uniform continuu daca
se zice uniform continuu daca

Teorema I.2.1. ( de caracterizare a semigrupurilor uniform continue Un semigrup S=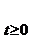 este uniform continuu daca
si numai daca generatorul sau infinitezimal A
este uniform continuu daca
si numai daca generatorul sau infinitezimal A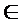 B(X).
B(X).
Corolarul I.2.1. Un semigrup S= 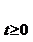 este uniform continuu daca si
numai daca exista un operator A
este uniform continuu daca si
numai daca exista un operator A  B(X) astfel incat
B(X) astfel incat
S(t) 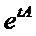 ,
, 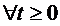 .
.
Teorema I.4.1. Fie S = un
un  - semigrup pe spatiul Banach X, iar A generatorul
sau infinetezimal. Atunci exista M
- semigrup pe spatiul Banach X, iar A generatorul
sau infinetezimal. Atunci exista M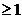 si
si  astfel incat
astfel incat
 ,
,  .
.
Teorema I.4.2.(Hille Yosida)
Fie A: D(A)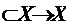 un operator liniar inchis si dens.
Daca exista M
un operator liniar inchis si dens.
Daca exista M si
si 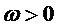 astfel incat
astfel incat
(i)
( )
) 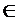
 (A);
(A);
(ii)
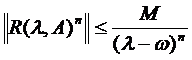 , pentru orice
, pentru orice 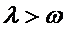 si
si
orice n atunci exista un C
atunci exista un C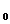 - semigrup S
- semigrup S  al
carui generator infinitezimal este A si cu proprietatea ca
al
carui generator infinitezimal este A si cu proprietatea ca




 ,
,
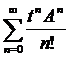 x.
x.
 ,
,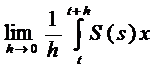 ds=S(t)x, pentru orice
x
ds=S(t)x, pentru orice
x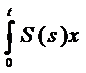 ds
ds 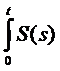 x
x ,
,