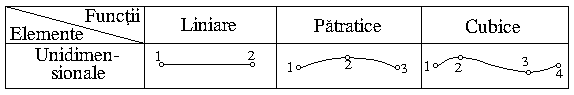Fundamentele teoretice ale metodei elementelor finite
I.Tipuri de
elemente finite
O
chestiune de maxima importanta in analiza numerica cu
metoda elementelor finite este alegerea celui mai potrivit tip de element finit si pentru aceasta
trebuie analizate urmatoarele aspecte:
-
forma elementului;
-
numarul si tipul de noduri;
-
tipul variabilelor nodale;
- tipul functiilor de
interpolare.
I.1. Forma
elementului finit determina
urmatoarea clasificare:
→elemente
unidimensionale - pot fi descrise de o singura variabila locala
independenta si sunt precizate prin doua (cel mai adesea) sau
mai multe noduri. Figura 1.1. prezinta astfel de elemente. Din
aceasta categorie de elemente finite fac parte elementele TRUSS, BEAMS,
PIPES, BELAS, din cadrul bibliotecii programului SAP-05, unul dintre cele mai
cunoscute si folosite programe de analiza prin metoda elementelor
finite din tara noastra, sau elementele TRUSS2D, TRUSS3D, BEAMS2D,
BEAMS3D, PIPE, din cadrul bibliotecii de elemente finite a programului COSMOS/M.
Fig. 1.1.
→elemente
bidimensionale - pot fi descrise prin
doua variabile locale independente si au minimum trei noduri,
numarul acestora putand ajunge in mod curent la opt; in figura 1..2 sunt
prezentate astfel de elemente finite.
Pentru
exemplificare, din cadrul aceluiasi program, SAP-05, pot fi amintite
elementele PLANE, PLANR, PLANM, PL8ND, PLMBR, SOLAX, SHELL, PLANI, SELAS. Din
biblioteca de elemente finite a programului COSMOS/M pot fi date ca exemplu
elementele PLANE2D, TRIANG2D, SHELL3, SHELL4 s.a.
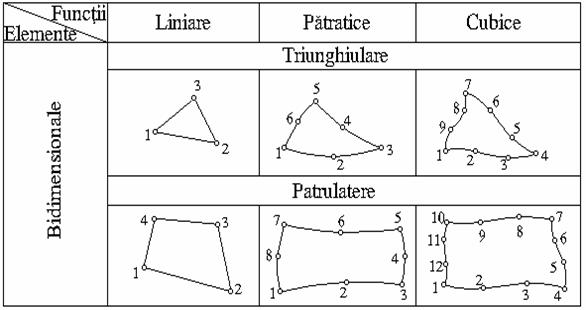
Fig. 1..2
→elemente
tridimensionale - pot fi descrise
prin trei variabile locale independente si au minimum patru noduri;
frecvent aceste elemente sunt reprezentate prin 8, 16 sau 20 de noduri. Din programul SAP-05, se pot da ca exemplu, elementele
THRED, THKSL sau BRK20, iar din cadrul programului COSMOS/M elementele TETRA
sau SOLID (figura 1.3).
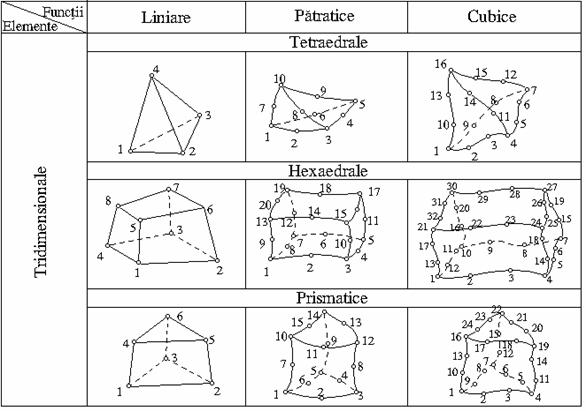
Fig.1.3.
I.2
Numarul si tipul nodurilor dau caracteristici functionale foarte
importante elementului finit. Nodurile pot fi: exterioare sau interioare. Cele
exterioare se gasesc pe frontiera (conturul) elementului si
reprezinta punctele de conexiune intre elementele vecine. Aceste noduri
sunt dispuse in colturile elementului sau in colturi si pe
laturi, asa cum se poate observa in figurile 1.1.2 si 1.1.3; nodurile
interioare sunt cele care nu se conecteaza cu elementele vecine. Un astfel
de nod este 'O' din figura 1.4.
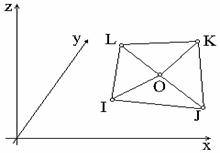 Fig. 1.4
Fig. 1.4
I.3. Tipul
variabilelor nodale (parametrilor asignati). Acestea pot fi exterioare sau interioare,
dupa cum este si nodul respectiv; variabilele nodale sunt, de fapt,
gradele de libertate (GDL: trei translatii si trei rotatii) ale
nodului, care sunt luate in consideratie.
I.4 Tipul
functiilor de interpolare determina
fundamental un element finit in modul lui de comportare, ca parte a structurii
cercetate. Functiile de interpolare sunt folosite pentru reprezentarea
variabilelor nodale in cadrul elementului finit; ele se mai numesc si
functii de forma sau functii de aproximare. Elementele care
folosesc aceleasi functii de interpolare, atat pentru descrierea
geometriei cu ajutorul coordonatelor x,y,z cat si pentru descrierea
deformatiilor cu ajutorul componentelor u,v,w se numesc elemente
izoparametrice. Majoritatea programelor de analiza prin metoda elementelor
finite folosesc astfel de elemente.
Elementele
izoparametrice au fost mentionate pentru prima data in literatura de
specialitate in anul 1966, intr-o lucrare a lui Irons B.M. Sistematizarea lor
si introducerea noilor concepte s-a facut de catre Zienkievicz,
in 1969.
Cand
geometria elementului finit este descrisa prin functii de ordin
inferior, iar campul deplasarilor prin functii de ordin superior,
elementul finit este numit subparametric
.
Toate
elementele subparametrice satisfac criteriile de convergenta, cat
si de compatibilitate a deplasarilor de-a lungul liniilor de
separatie intre elemente (functiile de aproximare ale
deplasarilor contin si pe cele ale geometriei elementului). Cand
geometria elementului finit este descrisa prin functii de ordin
superior, iar campul deplasarilor prin functii de ordin inferior,
elementul este numit superparametric.
Aceasta
familie de elemente finite nu a fost validata in intregime .
Functiile de interpolare nu pot fi alese arbitrar; ele trebuie sa
satisfaca o serie de cerinte pentru a se asigura criteriul de
convergenta, care este diferit, de regula, de la o problema
la alta (de la un element la altul).
Aceste
cerinte, care nu depind de calea de abordare pentru stabilirea
ecuatiilor metodei elementului finit, sunt:
- continuitatea;
- conformitatea (compatibilitatea);
- complinirea;
- invarianta.
I.5
Proprietatile functiilor de interpolare
CONTINUITATEA. Functiile de
modelare pentru deplasari trebuie sa fie continue, astfel incat
sa asigure variatii line ale campului deplasarilor pe tot
domeniul elementului finit, nepermitand salturi, goluri sau pante abrupte,
nici in interior si nici pe contur.
Atunci cand
continuitatea este numai la interfata dintre elementele invecinate, se numeste
continuitate de gradul zero, si se simbolizeaza 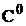
Daca
pe langa aceasta cerinta si prima derivata a
functiilor de interpolare asigura continuitatea, atunci avem de-a face
cu continuitate de gradul unu, cu simbolizarea 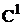 s.a.m.d. Pentru gradele de
libertate translatii, este suficienta continuitatea de gradul zero (
s.a.m.d. Pentru gradele de
libertate translatii, este suficienta continuitatea de gradul zero (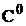 ), asigurata de functiile Lagrange; pentru gradele de libertate rotatii,
este necesara continuitatea de gradul unu (
), asigurata de functiile Lagrange; pentru gradele de libertate rotatii,
este necesara continuitatea de gradul unu (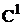
Elementele
finite, utilizate pentru calculul placilor incovoiate, necesita grade
de libertate translatii si rotatii, deci reclama
functii de interpolare de continuitate (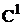 ); functia w(x,y) asigura continuitatea de-a lungul laturilor
elementului; continuitatea functiilor (
); functia w(x,y) asigura continuitatea de-a lungul laturilor
elementului; continuitatea functiilor (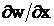 ) si (
) si (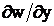 ) asigura continuitatea de-a lungul grosimii elementelor invecinate. Astfel de functii se
numesc de tip Hermite sau functii osculatoare. Cand se invoca
continuitatea de ordinul doi (
) asigura continuitatea de-a lungul grosimii elementelor invecinate. Astfel de functii se
numesc de tip Hermite sau functii osculatoare. Cand se invoca
continuitatea de ordinul doi (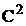 ), functiile de interpolare se numesc hiperosculatoare (necunoscutele nodale suplimentare sunt valorile
derivatelor de ordinul doi).
), functiile de interpolare se numesc hiperosculatoare (necunoscutele nodale suplimentare sunt valorile
derivatelor de ordinul doi).
Uneori,
se folosesc ca functii de interpolare seriile Fourier sau functiile
Spline.
CONFORMITATEA. Aceasta
proprietate cere ca, in timpul deformarii elementele vecine sa
ramana solidare de-a lungul frontierei comune. Atunci cand toate
cerintele de compatibilitate sunt satisfacute de functiile de
interpolare, elementele finite sunt conforme. In practica, se intalnesc
cerinte care duc la folosirea elementelor incompatibile. Acestea trebuie
folosite cu mare grija, necesitand experienta si chiar
unele testari; de regula, se recurge la un artificiu in descrierea
structurii, constand din folosirea pentru conexiunea elementelor bi- sau tri-
dimensionale de acest tip, a unor elemente unidimensionale (de exemplu BEAMS),
avand caracteristici care sa nu influenteze comportarea reala a
structurii discretizate.
COMPLINIREA In practica au fost si sunt folosite cu succes elemente
finite incompatibile, obtinandu-se rezultate care uneori sunt mai bune
decat in cazul folosirii celor compatibile. Cu cat este mai mare numarul
termenilor unei astfel de functii, cu atat convergenta este mai
stransa.
O functie de interpolare satisface conditia
de complinire daca contine moduri ale deplasarilor, care fac
posibile comportamentele atat de corp rigid cat si starile de
deformatii constante. O functie completa in acest sens
difera de o functie completa in sens matematic. Daca
functia de aproximare este incompatibila,
dar 'completa', convergenta solutiei este
obtinuta cu mult succes, in multe cazuri. Un mod de verificare a
convergentei solutiei este folosirea unor retele mai fine,
respectandu-se urmatoarele cerinte:
a)
fiecare discretizare anterioara trebuie sa se regaseasca in
cea noua;
b)
fiecare punct al structurii trebuie sa se afle totdeauna in cadrul unui
element finit;
c)
functia de interpolare sa ramana aceeasi, cand se
trece de la o retea (discretizare), la alta.
INVARIANTA. Aceasta
cerinta face ca elementul finit sa aiba aceeasi stare
de deformatie, oricare ar fi orientarea axelor de referinta
locale, in raport de care aceasta stare este formulata.
Cerinta
mai este cunoscuta si sub numele de izotropie geometrica sau spatiala
sau invarianta geometrica.
Pentru asigurarea acestei invariante, in functiile de interpolare se
opteaza pentru termenul 'xy' in loc de '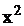 ' sau '
' sau ' ', ca al patrulea mod de deplasare, in cazul fuctiilor
polinomiale. Termenul 'xy' nu favorizeaza configuratia
deformatiilor pe nici una din cele doua directii: x sau y
(observatia este valabila si in cazul coordonatelor locale).
', ca al patrulea mod de deplasare, in cazul fuctiilor
polinomiale. Termenul 'xy' nu favorizeaza configuratia
deformatiilor pe nici una din cele doua directii: x sau y
(observatia este valabila si in cazul coordonatelor locale).
Bibliografie:
1. Dumitru N., Margine A., Organe de Masini. Asamblari. Elemente elastice.
Proiectare asistata de calculator. Editura Universitaria Craiova, 2002.
2. Pandrea ,N.,Rizea,V., Metoda elementelor finite. Concepte si aplicatii.
3. Pascariu,I., Elemente finite. Concepte si aplicatii. Editura Militara.
Bucuresti. 1985.
4.M. Blumenfeld - Introducere
in metoda elementelor finite, Ed. Tehnica, Bucuresti, 1995
5.E. Cuteanu, R. Marinov - Metoda elementelor finite in proiecterea structurilor, Ed. Facla, Timisoara, 1980
6.D. Garbea - Analiza
cu elemente finite, Ed. Tehnica, Bucuresti, 1990