Inele de fractii

Inele de fractii

O notiune importanta in teoria structurilor algebrice, in particular in teoria

inelelor, este aceea de scufundare izomorfa . Anume, vom spune ca inelul (A, +, ) se scufunda izomorf in inelul (B, +, daca exista un morfism injectiv f : A B .

Evident, in acest caz f(A) este un subinel al inelului B izomorf cu inelul A.

In leg a tura cu aceasta notiune este adevarata urmatoarea afirmatie:

Teorema 4.1. Fiecare inel se scufunda izomorf intr-un inel cu unitate.

Demonstratie. Fie inelul (A, +, si sa notam B = A x Z , unde Z este

multimea numerelor intregi. In multimea B s a definim doua operatii binare, notate tot prin + si astfel

(a1, n1) + (a2, n2) = (a1 + a2 , n1 + n2)

(a1, n1) (a2, n2) = (a1a2 + n2a1 , n1n2)

Se constata ca (B, +, este un inel care poseda ca element unitate perechea (0,1) .

Functia f : A B definita prin f(a) = (a, 0) este un morfism injectiv de la

inelul (A, +, la inelul (B, +, . Intr-adevar, faptul ca aceasta functie este injectiva este evident, apoi observam ca pentru orice a bI A

f(a + b ) = (a + b ,0 ) = (a, 0) + (b, 0) = f(a) + f(b)

f(ab) = (ab, 0) = (a, 0) (b, 0) = f(a) f(b) .

Prin urmare , inelul (A, +, ) se scufunda izomorf in inelul cu unitate  (B, + ,

O alta teorema de scufundare, deosebit de importanta in teoria inelelor, este

urmatoarea:

Teorema 4.2 Fie (A, +, ) un inel comutativ si cu element unitate si fie S

multimea tuturor elementelor din A care nu sunt divizori ai lui zero. Atunci exista inelul (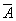 ) comutativ si cu element unitate si morfismul injectiv    f : A A astfel incat toate elementele din f(S) sunt inversabile in inelul (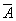

Demonstratie. Observam, mai intai, ca S Ø, deoarece cel putin elementul

unitate din inelul (A, +, ) apartine lui S (adica 1 I S ) si ca , daca s1, s2 I S, atunci s1s2 I S .

Apoi, se demonstreaza usor ca , relatia binara ~definita in produsul cartezian A x S prin

(a1, s1) (a2, s2) a1s2 = a2s1

este o relatie de echivalenta in multimea A x S . Deci, exista multimea cat    A x S ~ pe care sa o notam prin 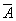, adica 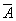, unde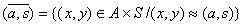

Definind in multimea cat A operatiile binare prin + si prin

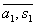
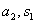
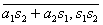
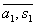
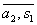
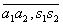
se constata ca operatiile de adunare si inmultire astfel definite nu depind de alegerea reprezentantilor claselor. Mai mult, (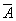 ), devine inel comutativ, care poseda ca element unitate clasa (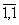

Functia f :A A, definita prin f( a) = (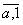 este un morfism injectiv de la inelul (A,+ , ) la inelul ( 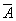) . Intr-adevar, daca f(a1) = f(a2) , atunci 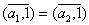, adica (a1,1) (a2.1), deci a1 1 = a2 1 si astfel a1 = a2 , prin urmare aplicatia f este injectiva . Apoi, observam ca oricare ar fi a1, a2 I A

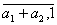
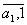
f (a1 + a2) = ( 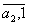) = f(a1) + f( a2) ,

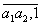
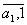
f (a1a2) = ( 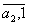) = f(a1) f(a2) .

Pentru a termina demonstratia, ramane sa aratam ca elementele din f(S) sunt

inversabile in inelul (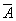 ) . Daca b I f(S) , atunci exista s I S astfel incat b = f(s)= (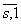) deci f(S) = . Cu aceasta precizare , observam ca oricare ar fi clasa (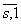 I f (S) , exista clasa (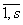 I A astfel incat ( (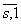

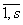
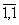
De obicei elementele inelului 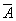se noteaza simplu prin , in loc de (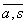) , adica 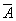= 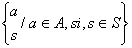. Acest inel se numeste inelul de fractii al inelului (A, +,

In cazul cand inelul (A, +, ) este domeniu de integritate, atunci inelul sau de

fractii (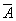 este chiar un corp, deci:

Teorema 4.3. Fiecare domeniu de integritate se scufunda izomorf intr-un

corp, numit corpul de fractii al domeniului de integritate respectiv.

Pentru exemplificare, sa ne reamintim cum a fost construit corpul

numerelor rationale (Q,+ , . Vom constata ca (Q,+ , ) este corpul de fractii al

domeniului de integritate (Z,+ ,