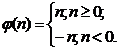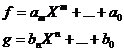Inele euclidiene
Definitia
2.1. Un inel integru A impreuna cu o functie 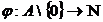 se numeste
inel euclidian daca are urmatoarele doua proprietati:
se numeste
inel euclidian daca are urmatoarele doua proprietati:
i)
Oricare ar fi elementele nenule a,b 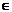 A astfel ca a sa divida pe b,
rezulta
A astfel ca a sa divida pe b,
rezulta 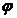 (a)
(a)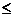
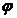 (b).
(b).
ii)
Pentru orice a,b 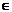 A, b
A, b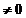 exista q,r
exista q,r 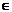 A astfel incat a=bq+r, unde r=0 sau
A astfel incat a=bq+r, unde r=0 sau 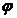 (r)<
(r)< 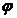 (b).
(b).
Ca exemplu de inele euclidiene avem
inelul intregilor Z pentru care functia 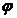 este valoarea
absoluta a numarului intreg:
este valoarea
absoluta a numarului intreg:
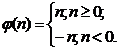
Se stie atunci ca
proprietatile i) si ii) din definitia de mai sus sunt
verificate. Proprietatea ii) in acest caz se numeste teorema
impartirii intregi, denumire pe care o vom pastra pentru orice
inel euclidian. Vom vedea in paragraful urmator ca de fapt numai
aceasta proprietate este esentiala in definitia de mai sus.
Observam ca in Z este
adevarata chiar o afimatie mai precisa decat conditia
ii) de mai sus. Anume, pentru a,b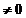 numere intregi exista q,r
numere intregi exista q,r 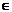 Z astfel incat a=bq+r, unde
Z astfel incat a=bq+r, unde 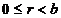 , care este numita de fapt teorema
impartirii intregi.
, care este numita de fapt teorema
impartirii intregi.
Orice corp este inel euclidian.
In adevar, daca k este un corp, consideram functia 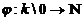 definita prin
definita prin 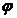 (a)=1, pentru orice a
(a)=1, pentru orice a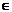 k, a
k, a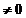 . Este evident ca aceasta
functie are proprietatile i) si ii).
. Este evident ca aceasta
functie are proprietatile i) si ii).
De
asemeanea, inelul 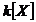 al
polinoamelor de o nedeterminata cu coeficienti in corpul k este
Euclidian daca consideram drept functie
al
polinoamelor de o nedeterminata cu coeficienti in corpul k este
Euclidian daca consideram drept functie 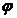 gradul unui polinom nenul.
gradul unui polinom nenul.
In
adevar, daca f,g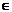
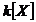 sunt polinoame nenule f|g, atunci g=ff' cu f'
sunt polinoame nenule f|g, atunci g=ff' cu f'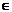
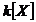 , deci grad g=grad f+grad f' si cum f'
, deci grad g=grad f+grad f' si cum f'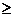 0, rezulta ca grad g
0, rezulta ca grad g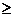 grad f, ceea ce verifica pe i).Pentru a
verifica pe ii) sa consideram f si g doua polinoame din
grad f, ceea ce verifica pe i).Pentru a
verifica pe ii) sa consideram f si g doua polinoame din 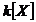 cu g
cu g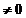 . Daca grad g=0 atunci f=g(g
. Daca grad g=0 atunci f=g(g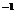 f) caci g este element diferit de zero
in k, deci inversabil si afirmatia este dovedita.
f) caci g este element diferit de zero
in k, deci inversabil si afirmatia este dovedita.
Putem
deci presupune ca grad g>0;atunci vom face o inductie dupa grad f.
Daca grad f<grad g, in particular pentru grad f=0, din relatia
f=g0 f rezulta ii). Presupunem acum ca ii) a fost
demonstrata pentru toate polinoamele f cu grad f<n. Fie atunci f un
polinom de grad n:
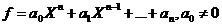
si
sa presupunem ca g este un polinom de grad m. Putem presupune ca
m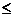 n, conform celor demonstrate mai sus. Fie:
n, conform celor demonstrate mai sus. Fie:

atunci
polinomul
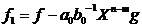
are
gradul cel mai mult n-1 si din ipoteza inductiva rezulta ca
exista q,r 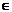
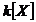 , astfel incat:
, astfel incat:
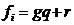 ,r=0 sau grad r<grad g.
,r=0 sau grad r<grad g.
Atunci
avem
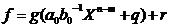
si
polinoamele 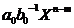 +q si r satisfac conditia ii).
+q si r satisfac conditia ii).
Un alt exemplu de inel euclidian
este inelul intregilor lui Gauss 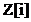 , in care functia
, in care functia 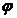 din definitie este norma N. In adevar, din
faptul ca norma produsului a doua elemente este egala cu
produsul normelor acestor elemente rezulta ca i) este
satisfacuta. Verificam conditia ii). Fie
din definitie este norma N. In adevar, din
faptul ca norma produsului a doua elemente este egala cu
produsul normelor acestor elemente rezulta ca i) este
satisfacuta. Verificam conditia ii). Fie 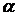 =a+a'i si
=a+a'i si 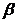 =b+b'i doua elemente din
=b+b'i doua elemente din 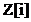 cu
cu 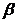
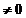 Atunci consideram elementul din Q
Atunci consideram elementul din Q :
:

care
se scrie sub forma 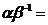 r+si, cu r,s
r+si, cu r,s 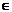 Q. Fie
Q. Fie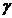 =c+c'i, unde c si c' sunt cele mai apropiate numere
intregi de r, respectiv s si
=c+c'i, unde c si c' sunt cele mai apropiate numere
intregi de r, respectiv s si  =r-c+(s-c')i. Avem atunci relatia
=r-c+(s-c')i. Avem atunci relatia 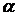 =
=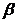
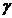 +
+
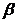 si deoarece
si deoarece 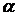 si
si 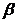
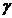
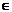
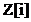 (fiindca
evident
(fiindca
evident 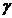
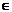
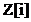 ), avem
), avem 
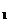 =
=
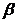
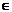
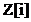 . Avem totodata N(
. Avem totodata N(
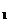 )=
)=
=N(
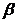 )=N(
)=N( )N(
)N(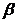 )=((r-c)
)=((r-c)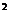 +(s-c')
+(s-c')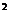 )N(
)N(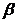 )
)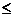
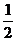 N(
N(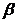 ), caci
), caci 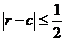 si
si 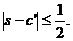 De aici rezulta ca este satidfacuta
si conditia ii).
De aici rezulta ca este satidfacuta
si conditia ii).
In mod analog putem sa
aratam ca inelul 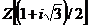 este inel euclidian. Acest inel este cel mai mic
subinel al corpului numerelor complexe C care contine elementul
este inel euclidian. Acest inel este cel mai mic
subinel al corpului numerelor complexe C care contine elementul  . Se vede imediat ca elementele lui
. Se vede imediat ca elementele lui 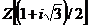 sunt toate
numerele complexe de forma
sunt toate
numerele complexe de forma
a+b . Corpul de fractii al acestui inel este corpul Q
. Corpul de fractii al acestui inel este corpul Q , care este constituit din toate numerele complexe de
forma r+s
, care este constituit din toate numerele complexe de
forma r+s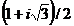 , cu r,s
, cu r,s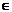 Q. Definim norma unui numar din acest corp punand pentru
Q. Definim norma unui numar din acest corp punand pentru
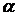 =r+s
=r+s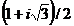 ,
, 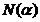 =(r+s
=(r+s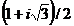 )(r+s
)(r+s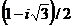 =
=
=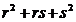 . Se verifica usor relatia:
. Se verifica usor relatia:
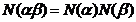 pentru orice
pentru orice 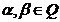
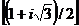 .
.
Evident ,restictia lui N la 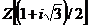 este o
functie de la acest inel in N. Din relatia (1) de mai sus
rezulta ca proprietatea i) din definitia inelului euclidian este
satisfacuta. Pentru a verifica cea de-a doua proprietate, procedam
ca si in cazul inelului intregilor lui Gauss. Fie
este o
functie de la acest inel in N. Din relatia (1) de mai sus
rezulta ca proprietatea i) din definitia inelului euclidian este
satisfacuta. Pentru a verifica cea de-a doua proprietate, procedam
ca si in cazul inelului intregilor lui Gauss. Fie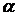 si
si 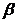 doua elemente din
doua elemente din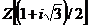 ;atunci elementul
;atunci elementul 
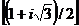 , deci se scrie sub forma
, deci se scrie sub forma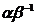 = r+s
= r+s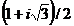 . Fie
. Fie 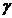 =c+c'
=c+c' , unde c si c' sunt cele mai apropiate
numere intregi de r, respective s si
, unde c si c' sunt cele mai apropiate
numere intregi de r, respective s si  =r-c+(s-c')
=r-c+(s-c')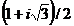 . Avem atunci relatia
. Avem atunci relatia 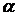
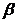
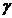

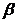 si , deoarece
si , deoarece 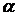 si
si 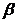
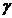 apartin lui
apartin lui 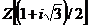 , rezulta ca:
, rezulta ca:

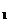 =
=
Dar
N(
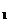 )=N(
)=N(
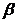 )=N(
)=N( )N=
)N=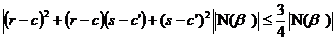 caci
caci
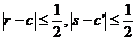 . De aici rezulta ca este
satisfacuta conditia ii).
. De aici rezulta ca este
satisfacuta conditia ii).
Propozitia
2.2. Intr-un inel euclidian orice doua elemente au un cel mai mare
divizor comun si un cel mai mic multiplu comun.
Demonstratie.Pentru a demonstra
aceasta propozitie vom utiluza rationamentul care se face de
obicei pentru a arata ca pentru Z este adevarata
afirmatia, adica vom aplica succesiv teorema impartirii
intregi, ceea ce se numeste
algoritmul lui Euclid. Fie a, b doua elemente din inelul euclidian A.
Daca unul dintre aceste elemente este nul, atunci se observa ca
celalalt este un cel mai mare divizor comun al lor. Deci putem presupune a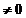 ,b
,b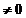 . Aplicam teorema impartirii intregi
elementelor a si b si obtinem a=bq
. Aplicam teorema impartirii intregi
elementelor a si b si obtinem a=bq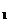 +r
+r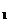 , unde r
, unde r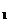 =0 sau
=0 sau  (r
(r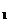 )<
)<  (b), apoi daca r
(b), apoi daca r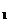
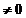 , aceeasi teorema o aplicam elementelor
b si r
, aceeasi teorema o aplicam elementelor
b si r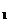 , b= r
, b= r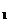 q
q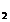 +
+ , unde
, unde  =0 sau
=0 sau
 (
( )<
)<  ( r
( r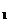 ); daca
); daca 
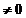 obtinem analog r
obtinem analog r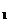 =
=  q
q +r
+r , cu r
, cu r =0 sau
=0 sau  (r
(r )<
)< (
( ) si se continua mereu daca restul
obtinut este diferit de zero. Deoarece sirul
) si se continua mereu daca restul
obtinut este diferit de zero. Deoarece sirul  ( r
( r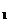 )>
)> (
( )> este un sir descrescator de numere
naturale, dupa un numar finit de pasi obtinem neaparat
un rest nul si atunci obtinem niste relatii de forma:
)> este un sir descrescator de numere
naturale, dupa un numar finit de pasi obtinem neaparat
un rest nul si atunci obtinem niste relatii de forma:

unde
r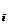
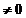 , i=1, . ,n. Sa aratam ca r
, i=1, . ,n. Sa aratam ca r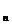 este cel mai mare divizor comun al
elementelor a si b.
este cel mai mare divizor comun al
elementelor a si b.
Din
relatiie (2) se vede ca r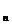 divide pe r
divide pe r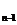 , apoi ca r
, apoi ca r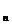 divide pe r
divide pe r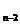 , r
, r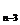 etc. Deci r
etc. Deci r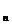 divide pe a si b. Fie acum c un divizor
comun al lui a si b. Atunci din relatiile (2) rezulta ca c
divide pe
divide pe a si b. Fie acum c un divizor
comun al lui a si b. Atunci din relatiile (2) rezulta ca c
divide pe 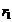 , apoi c divide pe
, apoi c divide pe 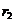 etc.
Adica c divide pe r
etc.
Adica c divide pe r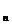 . A doua afirmatie a propozitiei
rezulta din cea precedenta si din propozitia 1.9. Din
propozitia precedenta si din propozitia 1.15 rezulta:
. A doua afirmatie a propozitiei
rezulta din cea precedenta si din propozitia 1.9. Din
propozitia precedenta si din propozitia 1.15 rezulta:
Corolarul 2.3.
Intr-un inel Euclidian orice element ireductibil este prim.
De aici deducem ca inelul 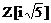 nu este inel
Euclidian caci in 1 am aratat ca 3 este ireductibil, insa
nu este prim in acest inel.
nu este inel
Euclidian caci in 1 am aratat ca 3 este ireductibil, insa
nu este prim in acest inel.
Daca A este un inel integru
care nu este corp, vom arata in 3 ca A[X] nu este
euclidian.Totusi o afirmatie analoaga proprietatii ii)
din definitia 2.1. este adevarata si in acest caz.
Propozitia 2.4 Fie A un inel
si A[X] inelul polinoamelor de o nedeterminata cu
coeficientii in A. Fie
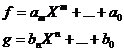
doua
polinoame din A[X]de grad m, respectiv n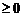 , deci b
, deci b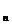
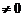 si k =max(m-n+1,0). Atunci exista polinoame q
si r din A[X] astfel ca
si k =max(m-n+1,0). Atunci exista polinoame q
si r din A[X] astfel ca

cu
grad r<n. In plus, daca b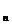 este nondivizor al lui zero, atunci q si r sunt
unic determinate.
este nondivizor al lui zero, atunci q si r sunt
unic determinate.
Demonstratie. Pentru m<n luam q=0, k=0
si r=0. Pentru m=n=k=0, rezulta k=1 si putem lua q=a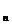 , r=0; pentru m
, r=0; pentru m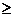 n-1, k=m-n+1 si vom demonstra prima afirmatie
a propozitiei prin inductie dupa m. Pentru m=n-1, k=0 si
putem lua q=0 si r=f. Fie m
n-1, k=m-n+1 si vom demonstra prima afirmatie
a propozitiei prin inductie dupa m. Pentru m=n-1, k=0 si
putem lua q=0 si r=f. Fie m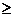 n. Atunci polinomul f
n. Atunci polinomul f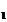 =
=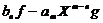 are gradul cel mai mult m-1, deci exista, din
ipoteza inductiva, polinoamele q
are gradul cel mai mult m-1, deci exista, din
ipoteza inductiva, polinoamele q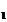 si r
si r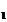 , astfel ca
, astfel ca
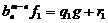 unde grad r
unde grad r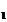 <n.
<n.
Atunci
pentru f este suficient sa consideram 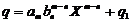 si r= r
si r= r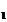 .
.
Sa presupunem acum ca  . Atunci rezulta (q'-q)g=r'-r. Daca q'=q,
atunci evident si r'=r. Daca q'
. Atunci rezulta (q'-q)g=r'-r. Daca q'=q,
atunci evident si r'=r. Daca q'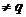 , atunci din faptul ca b
, atunci din faptul ca b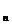 este nondivizor al lui zero rezulta ca gradul
polinomului din membrul stang este
este nondivizor al lui zero rezulta ca gradul
polinomului din membrul stang este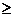 n, iar cel din membrul drept <n, absurd.
n, iar cel din membrul drept <n, absurd.
Mentionam ca uneori
notiunea de inel euclidian este data intr-un sens putin diferit.
Anume, un inel integru A impreuna cu o functie 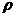
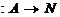 se numeste
euclidian daca
se numeste
euclidian daca 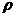 are
urmatoarele proprietati:
are
urmatoarele proprietati:
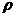 (a)=0 daca si numai daca a=0;
(a)=0 daca si numai daca a=0;
Pentru a,b 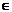 A,
A, 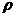 (ab)=
(ab)= 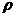 (a)
(a) 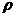 (b);
(b);
Pentru a,b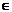 A nenule exista q si r
A nenule exista q si r 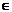 A, astfel ca
A, astfel ca
a=bq+r,
cu 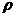 (r)<
(r)< 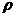 (b)
(b)
Observam ca din 2)
rezulta ca 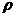 satisface prima
proprietate din definitia 2.1 si deci un inel euclidian in sensul
definitiei de mai sus este euclidian si in sensul definitiei
2.1. De asemenea, toate exemplele de inele euclidiene care le-am dat satisfac
conditiile 1),2) si 3) de mai sus. In adevar, pentru Z
satisface prima
proprietate din definitia 2.1 si deci un inel euclidian in sensul
definitiei de mai sus este euclidian si in sensul definitiei
2.1. De asemenea, toate exemplele de inele euclidiene care le-am dat satisfac
conditiile 1),2) si 3) de mai sus. In adevar, pentru Z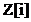 si
si 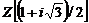 valeoarea
absoluta, norma, respectiv valoarea absoluta a normei, satisfac
conditiile 1),2) si 3) dupa cum am verificat. In cazul unui inel
de polinoame cu coeficienti intr-un corp, se considera functia
valeoarea
absoluta, norma, respectiv valoarea absoluta a normei, satisfac
conditiile 1),2) si 3) dupa cum am verificat. In cazul unui inel
de polinoame cu coeficienti intr-un corp, se considera functia 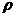 (f)=
(f)= , unde a >1 este un numar intreg si se verifica usor ca
are proprietatile 1),2),3).
, unde a >1 este un numar intreg si se verifica usor ca
are proprietatile 1),2),3).
La sfarsitul paragrafului
urmator vom arata ca in definitia 2.1 putem lasa la o
parte conditia i).
Mai mentionam, de
asemenea, ca in proprietatile demonstrate aici de spre inelele
euclidiene si in teorema 3.2 nu s-au folosit alte proprietati
ale lui N decat faptul ca ordinea obisnuita N este o
multime bineordonata, incat in definitia 2.1 putem sa
inlocuim pe N cu o multime bineordonata arbitrara.