REGRESIE
SI CORELATIE
Legaturile care
exista intre doua variabile statistice pot fi studiate folosind
doua tehnici: regresia si corelatia. Corelatia va arata cat de puternica este
legatura, dependenta dintre variabile, in timp ce regresia va ajuta in explicarea si
previzionarea unui factor pe baza valorii altuia (altora), ceea ce, evident, va
reduce incertitudinea privitoare la fenomene importante, dar aleatoare. In
sens statistic, termenul regresie ii apartine statisticianului
englez F. Galton (1822-1911).
Exista trei
scopuri principale, atunci cand analizam legaturile dintre variabile
statistice:
. sa descriem si sa intelegem
relatiile de dependenta;
. sa prognozam o noua valoare a variabilei
efect;
. sa ajustam si sa controlam
variabila efect, prin interventia asupra variabilei cauza.
RECAPITULARE
I. Breviar
teoretic
a) Media aritmetica
Media aritmetica sintetizeaza intr-o
singura valoare, toate valorile individuale observate.
simpla 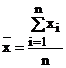
ponderata 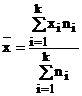
b) Indicatori statistici ai
imprastierii
1. Indicatori simpli ai
variatiei
Prin intermediul
indicatorilor simpli ai variatiei se caracterizeaza
imprastierea elementelor seriei de repartitie studiate
fata de medie, sau fata de un anumit element al seriei.
Indicatorii simpli
ai variatiei sunt: amplitudinea si abaterile elementelor seriei
fata de media lor.
1.1 Amplitudinea
Amplitudinea (A)
exprima, in marimi absolute marimea intervalului in care sunt
distribuite elementele seriei de repartitie. Amplitudinea absoluta se
calculeaza ca diferenta intre cel mai mare si cel mai mic
element al seriei.
A=xmax-xmin
Daca seriile de
distributie se repartizeaza pe intervale egale sau neegale,
amplitudinea (A) se calculeaza ca diferenta intre limita
superioara a ultimului interval si limita inferioara a primului
interval.
1.2 Abaterea
individuala
Abaterea elementelor
seriei fata de media lor se obtine in cifre absolute, ca
diferenta intre fiecare element al seriei (xi) si
media acestora (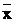 ), astfel:
), astfel:
di
= xi - 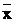
Abateri maxime: dmax = xmax - 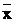
Abateri minime:
dmin = xmin - 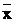
di(%) = 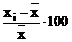 ; dmax(%)
=
; dmax(%)
=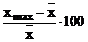 dmin(%)
=
dmin(%)
=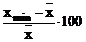
1.3 Variatia quartilica
Variatia
quartilica absoluta VQa = Q3 - Q1
Evidentiaza campul de imprastiere a 50% din
unitatile populatiei
Variatia
quartilica relativa 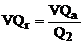
1.4 Variatia decilica
Variatia
decilica absoluta: VDa = D9 - D1
Evidentiaza campul de imprastiere a 80% din
unitatile populatiei
Variatia
decilica relativa: 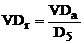
Masoara cu cat se abate in medie fiecare varianta din cele
80% unitati de la valoarea centrala (D5 sau Me)
2. Indicatori sintetici ai
variatiei
Indicatorii sintetici sunt
marimi medii calculate din abaterile variantelor caracteristicii de la
nivelul mediu al acesteia.
2.1 Abaterea medie liniara
Abaterea medie
liniara (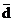 ) se calculeaza ca medie aritmetica, simpla
sau ponderata, in functie de felul seriei, din valorile absolute ale
abaterilor variantelor caracteristicii de la media lor.
) se calculeaza ca medie aritmetica, simpla
sau ponderata, in functie de felul seriei, din valorile absolute ale
abaterilor variantelor caracteristicii de la media lor.
Pentru o serie simpla: 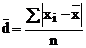
Pentru
o serie de distributie: 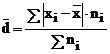
2.2 Dispersia
Dispersia
reprezinta media patratica simpla sau ponderata a
abaterilor variantelor caracteristicii de la media lor.
Pentru o serie simpla: 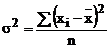
Pentru
o serie de distributie: 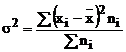
2.3 Abaterea medie patratica
Pentru o serie simpla: 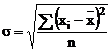
Pentru o serie de distributie: 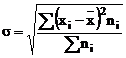
2.4 Coeficientul de variatie
Coeficientul de variatie este
indicatorul folosit pentru comparatia unor caracteristici diferite si
analiza variatiei aceleiasi caracteristici in doua colectivitati
in care variantele caracteristicii au ordine de marime diferita.
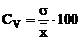 ;
; 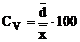
Daca
CV = 0, inseamna lipsa de variatie, valorile sunt
egale intre ele si egale cu media lor;
Daca
CV 0 variatia caracteristicii este mica;
Daca
CV 100% variatia caracteristicii este mare.
Intervalul de variatie al lui CV se poate imparti
astfel:
0<
CV T variatie mica care se
caracterizeaza prin:
- media este semnificativa, deoarece abaterile elementelor seriei de
la medie sunt mici;
- colectivitatea este omogena
35%
< CV T variatie relativ mare
50%<
CV T variatie foarte mare ceea ce
inseamna ca:
- media calculata nu este semnificativa
- colectivitatea este eterogena
- se va reface gruparea unitatilor.
c) Metode
statistice de analiza a legaturilor dintre fenomene
Analiza legaturilor
dintre fenomenele si procesele social-economice are ca punct de plecare
punerea in evidenta a existentei legaturilor. Dintre cele
mai importante metode de evidentiere a existentei si formei
legaturilor, prezentam: metoda seriilor paralele de date
interdependente, metoda gruparilor, metoda analizei dispersionale, metoda
grafica, metoda functiei de regresie.
1 Metoda seriilor paralele de date interdependente
Metoda seriilor paralele de date interdependente consta in prezentarea
paralela a datelor referitoare la mai multe caracteristici. Prin
compararea sirurilor de date se constata daca schimbarea
valorilor unei caracteristici este determinata in mod sistematic de
schimbari in variatia altei caracteristici. Aceasta metoda
se foloseste numai cand avem un numar mic de unitati
observate.
2 Metoda grafica
Metoda grafica pune in evidenta cel mai bine sensul si
forma legaturii dintre indicatorii a caror dependenta se
studiaza din punct de vedere statistic.
In cazul
reprezentarii grafice se intalnesc urmatoarele situatii:
in cazul in care punctele sunt dispersate
la intamplare rezulta ca intre cei doi indicatori nu exista o
legatura semnificativa. Aceasta situatie este
prezentata in figura 1. Linia trasa prin mijlocul norului de puncte
este, in general, paralela cu axa absciselor.
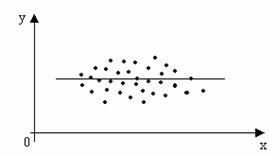
Fig. 1 Legatura nesemnificativa
daca punctele se disperseaza in
directia unei anumite linii care nu este paralela cu axa "ox",
rezulta ca cele doua caracteristici sunt corelate. In cazul in
care linia in jurul careia se concentreaza punctele este o linie
dreapta rezulta ca legatura dintre cele doua caracteristici
este rectilinie. Daca intre cele doua caracteristici exista o
legatura curbilinie aceasta linie este o curba
(parabola, hiperbola, exponentiala etc).
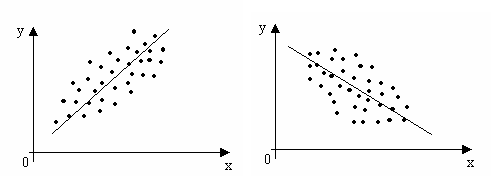
Fig. 2 Legatura directa Fig. 3
Legatura inversa
3 Metoda functiilor de
regresie
Metoda
functiilor de regresie exprima sub forma algoritmica modul
in care modificarea caracteristicii rezultative (y) este determinata de
modificarea caracteristicii factoriale (x).
y = f(x1, x2, . , xn)
3.1 Regresie simpla liniara
Regresia simpla liniara apreciaza forma dependentei
caracteristicii rezultative (y) de variatia caracteristicii factoriale
(x), adica: Yx = a+bx
unde: x
- valorile empirice ale caracteristicii factoriale
b - indica panta liniei. In
corelatia inversa acest parametru are o valoare
negativa, iar in
cazul corelatiei directe, o valoare pozitiva.
Estimarea
parametrilor se realizeaza prin metoda celor mai mici patrate.
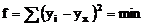 T
T 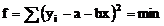
Se deriveaza
relatia de mai sus in functie de parametrul "a" si parametrul
"b":
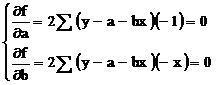 T
T 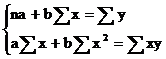
Se
calculeaza parametrii "a" si "b":
3.2 Regresia simpla curbilinie
Parabola T Yx = a+bx+cx2
Hiperbola T 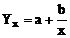
Exponentiala T Yx = abx
Masurarea intensitatii legaturilor statistice
Masurarea
intensitatii legaturii dintre indicatorii economici, a gradului
de determinatie dintre doua sau mai multe caracteristici, poate ajuta
la ierarhizarea unor factori ce influenteaza rezultatele economice,
participand, alaturi de alte procedee si tehnici de analiza
cantitativa a fenomenelor, la fundamentarea unor decizii economice.
Indicatorii folositi pentru a
masura intensitatea legaturii sunt: covarianta; coeficientul de
corelatie; raportul de corelatie.
Covarianta
Covarianta
este indicatorul cu ajutorul caruia se calculeaza legatura
dintre o caracteristica factoriala (x) si o caracteristica
rezultativa (y).
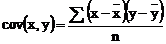
Daca
legatura este directa atunci indicatorul are valoare pozitiva
iar daca legatura este de tip invers, atunci indicatorul are valoare
negativa. Covarianta este nula daca variabilele sunt
independente.
2 Coeficientul de corelatie
Coeficientul
de corelatie simpla masoara intensitatea legaturii
dintre doua variabile xi si yi.
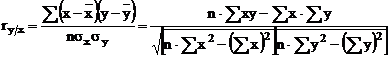
Coeficientul
de corelatie poate lua valori cuprinse intre - 1 si +1, adica
satisface inegalitatea: 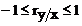 .
.
Cand 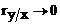 legatura este
apreciata ca slaba
legatura este
apreciata ca slaba
Cand 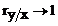 legatura este
apreciata ca puternica
legatura este
apreciata ca puternica
Daca
ia valori pozitive 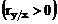 legatura este
directa, daca ia valori negative
legatura este
directa, daca ia valori negative 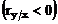 legatura este
inversa.
legatura este
inversa.
Valoarea
coeficientului de corelatie depinde de forma liniei de regresie, deci in
cazul legaturilor neliniare este putin semnificativ, pentru aceasta
se foloseste raportul de corelatie.
3 Raportul de corelatie
Raportul
de corelatie masoara intensitatea legaturii dintre
doua variabile xi si yi.
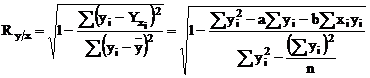
Raportul
de corelatie ia valori cuprinse intre 0 si 1, adica satisface
inegalitatea: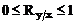 . Semnul raportului de corelatie este dat de semnul
coeficientului de regresie (b) din cadrul functiei de regresie.
. Semnul raportului de corelatie este dat de semnul
coeficientului de regresie (b) din cadrul functiei de regresie.
Raportul
de corelatie masoara intensitatea legaturilor indiferent de
forma de legatura.
d) Serii cronologice
Pentru ca seriile cronologice sa isi poata indeplini
functia de a caracteriza cat mai exact variatia fenomenelor in timp,
se folosesc indicatori absoluti, relativi si medii.
Indicatorii
seriilor cronologice
Indicatorii absoluti ai
seriilor cronologice
Ei redau starea fenomenului intr-o anumita
perioada sau modificarile de nivel survenite in decursul timpului. Se
deosebesc doua grupe de indicatori:
indicatori
de nivel (yt) care exprima marimea, cuantumul inregistrat
de fenomenul analizat in unitatea de timp t.
indicatori
ai modificarii absolute (D) redau in marimi absolute cuantumul
modificarii in timp a nivelului caracteristicii
Indicatorii modificarii absolute pot fi
determinati astfel:
modificarea
cu baza fixa: 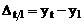 ,
,
unde: t=2, 3, . , n iar y1
reprezinta nivelul perioadei de referinta
modificarea
cu baza in lant: 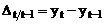 ; t=2, 3, . , n
; t=2, 3, . , n
2.
Indicatori relativi ai seriilor cronologice
Acesti indicatori redau proportia
nivelului, respectiv proportia decalajului realizat intr-o anumita
perioada fata de nivelul baza de raportare.
2.1 Indicii de modificare
Indici
de crestere cu baza fixa: 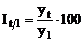 t=2,3, . , n
t=2,3, . , n
Indici
de crestere cu baza in lant: 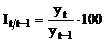 ; t=2,3, . , n
; t=2,3, . , n
2.2. Ritmul de dinamica exprima sub forma de
marimi relative sporul sau scaderea realizata in fiecare
perioada fata de nivelul considerat baza de raportare.
In raport cu baza de raportare, ritmul dinamicii
poate fi determinat cu baza fixa sau cu baza in lant.
Ritmul
dinamicii cu baza fixa, se obtine cu relatia: 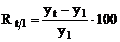 ; sau
; sau
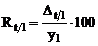 si arata cu cat la suta a crescut
nivelul variabilei analizate in intervalul de timp considerat.
si arata cu cat la suta a crescut
nivelul variabilei analizate in intervalul de timp considerat.
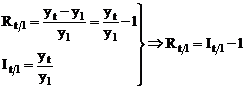
Ritmul
dinamicii cu baza in lant, se obtine cu relatia: 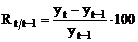 ; sau
; sau 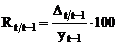
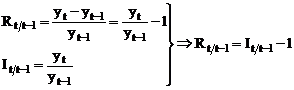
sau 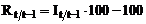
3 Indicatorii medii ai seriilor cronologice
Acesti indicatori
redau fie nivelul central al caracteristicii, fie cresterea medie
inregistrata de fenomenul analizat in decursul timpului.
Determinarea nivelului mediu pentru o serie
construita din indicatori de nivel:
nivelul
mediu al variabilei 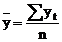
modificarea medie absoluta
(sporul 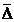 )
)
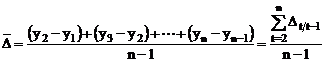
sau
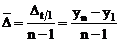 pentru baza
fixa
pentru baza
fixa
- indicele mediu 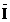
Indicele mediu de crestere sau scadere
(I) exprima proportia medie pe care o reprezinta, pentru
perioada succesiva, nivelul variabilei analizate.
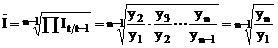
unde n este numarul de termeni in sir.
Daca:
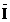 < 100% indicele mediu semnalizeaza scaderea sau
reducerea fenomenului analizat;
< 100% indicele mediu semnalizeaza scaderea sau
reducerea fenomenului analizat;
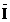 > 100% indicele
mediu semnalizeaza cresterea fenomenului analizat
> 100% indicele
mediu semnalizeaza cresterea fenomenului analizat
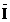 =100% indicele mediu arata ca fenomenul cercetat nu
prezinta evolutie, ci stationeaza.
=100% indicele mediu arata ca fenomenul cercetat nu
prezinta evolutie, ci stationeaza.
- ritmul mediu de crestere sau
scadere (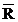 )
)
Ritmul mediu de
crestere sau scadere (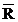 ) arata cu cat creste sau scade in medie variabila
yt in perioada analizata.
) arata cu cat creste sau scade in medie variabila
yt in perioada analizata.
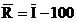
Metode de determinare si analiza a trendului (ajustarea seriilor
cronologice)
Pentru ajustarea seriilor cronologice se folosesc
mai multe procedee: ajustarea pe baza mediilor mobile, ajustarea prin metoda
grafica, ajustarea pe baza sporului mediu, ajustarea indicelui mediu,
ajustarea prin metode analitice.
Ajustarea prin metoda grafica
Se construieste un grafic in care se
prezinta seria initiala de date, dupa care se unesc
printr-o linie dreapta termenii extremi ai seriei in asa fel incat
linia dreapta sa inregistreze abateri minime fata de
termenii reali, dispusi in grafic.
Ajustarea seriilor cronologice ne ofera mai
clar tendinta de evolutie in timp a fenomenelor si proceselor
economice.
Ajustarea pe baza modificarii medii
absolute mediu
Se foloseste cand termenii seriei au
tendinta de crestere sub forma unei progresii aritmetice.
Intre primul termen al seriei cronologice
initiale sporurile cu baza in lant si ultimul termen
exista urmatoarea relatie:
xn= x0+D D D Dn/n-1
Considerand ca sporurile cu baza in lant
inregistreaza o valoare mica fata de sporul mediu si
se pot compensa reciproc, atunci relatia de mai sus devine:
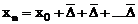
Suma sporurilor medii se
transforma intr-un produs de medii, iar relatia dintre primul termen
si sporurile medii devine:
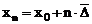
Daca se considera variatia de timp
(t) dupa care se manifesta termenii seriei dintre primul termen
si sporurile medii devine:
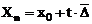 ;
t=0,1,2,3 . .n
;
t=0,1,2,3 . .n
Tabelul
1
|
Timp
|
Nivelul
|
Variatia de timp (t)
|
Valoarea teoretica
(ajustata) pe baza sporului mediu
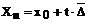
|
|
T0
|
x0
|
|
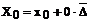
|
|
T1
|
x1
|
|
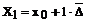
|
|
T2
|
x2
|
|
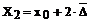
|
|
|
|
|
|
Tn
|
xn
|
n
|
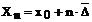
|
Ajustarea pe baza metodei indicelui mediu
Se foloseste cand termenii seriei se
manifesta sub forma unei progresii geometrice, iar ratia este considerata indicele
mediu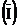 .
.
Intre ultimul termen al seriei, indicii cu baza in
lant in primul termen exista relatia: xn = x0·I1/0·I2/1·I3/2 . In/n-1
In situatia in care indicii cu baza in
lant au valori apropiate intre ei, pot fi inlocuite cu indicele mediu 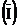 ;
;
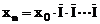 T
T 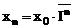
unde n - numarul unitatilor de timp corespunzatoare
pozitiei fata de termenul de baza.
Formula de calcul a unui termen ajutat poate
devine:
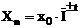
Tabelul
2
|
Timp
|
Nivelul
|
Variatia de timp (t)
|
Valoarea teoretica
(ajustata) pe baza indicelui mediu 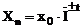
|
|
T0
|
x0
|
|
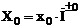
| |
|
T1
|
x1
|
|
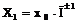
| |
|
T2
|
x2
|
|
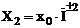
| |
|
|
|
| |
|
Tn
|
xn
|
n
|
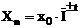
| |
| | | | | | | | |
Ajustarea prin metode analitice
Seriile
cronologice sunt prezentate prin, n termeni care esalonati
succesiv dupa o caracteristica de timp descriu evolutia
empirica a fenomenului respectiv.
In
obtinerea configuratiei noilor serii cronologice un rol deosebit il
au primul si ultimul termen ai seriilor initiale.
Pentru
valorificarea influentei termenilor intermediari ai seriei cronologice
care inregistreaza abateri si pot influenta modificarea
sistematica fata de evolutia fenomenelor, se folosesc
metode analitice.
Considerand
seria cronologica o variabila de timp ce se formeaza ca o
functie liniara, exponentiala sau hiperbolica
relatiile de calcul se pot sintetiza prin:
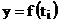
unde t - timpul (valori independente)
y - fenomenele prezentate in
serie.
Functia
liniara va fi utilizata atunci cand graficul prin care se
prezinta seria empirica indica
o tendinta de crestere absoluta prin sporuri cu baza
in lant, apropiate intre ele.
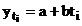
unde: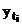 - valorile teoretice ale caracteristicii ce trebuie
ajutata
- valorile teoretice ale caracteristicii ce trebuie
ajutata
a - parametrul cu sens de marime medie
b - parametrul care indica
influenta caracteristicii factoriale (t) si indica panta liniei
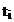 - valorile caracteristicii factoriale.
- valorile caracteristicii factoriale.
Functia
exponentiala se foloseste cand graficul arata o
tendinta de crestere relativ, constanta, respectiv
cresterii absolute din ce in ce mai mari, verificata si prin
obtinerea unor valori apropiate ale
indicilor cu baza in lant.
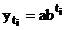
Ecuatia de estimare a unei parabole de gradul 2
exprimata in functie de timp este:
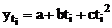
pentru aflarea parametrilor functiei de
regresie necesara ajutarii seriei se aplica metoda celor mai
mici patrate, adica:
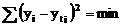 T
T 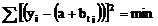
Se determina valorile
parametrilor a si b.
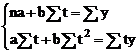
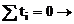 conditie
conditie
pentru 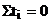 sistemul devine:
sistemul devine: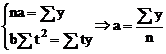 ;
; 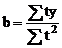
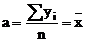
In
cazul cand seria este formata dintr-un numar impar de termeni
originea valorilor de timp va fi chiar termenul central si variatia
de timp se va masura in intervale intregi: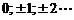
In
cazul unei serii dinamice formate dintr-un numar par de termeni, originea
valorilor de timp va cadea intre cei doi termeni centrali si
variatia de timp se va masura in jumatati de intervale
de timp: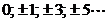
Prin
ajustare s-au redistribuit influentele factoriale astfel: toti
factorii au fost considerati cu influenta constata pe
toata perioada si variabil a fost numai timpul.
APLICATIE
RECAPITULATIVA
Se cunosc urmatoarele date privind incasarile medii lunare
si suprafata comerciala a 10 societati comerciale
avand acelasi profil de activitate:
Tabelul
3
|
Suprafata
comerciala
(mp)
|
|
|
|
|
|
|
|
|
|
|
|
Incasarile
medii lunare
(mil. lei)
|
|
|
|
|
|
|
|
|
|
|
Se cere:
- Sa se
calculeze suprafata medie comerciala si incasarile
medii lunare pentru cele 10 societati comerciale;
- Sa se
calculeze abaterea societatilor comerciale fata de
valoarea medie;
- Sa se
stabileasca tipul de legatura dintre suprafata
comerciala si incasarile medii lunare;
- Sa se
calculeze valorile ajustate ale incasarilor fata de
suprafata comerciala;
- Sa se
masoare intensitatea legaturii dintre suprafata
comerciala si incasarile medii lunare;


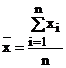
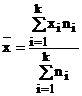
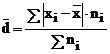
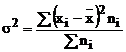
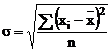
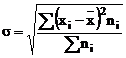


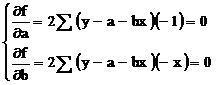
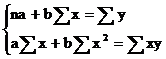
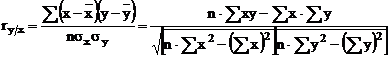
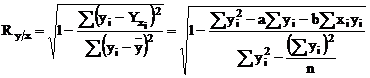
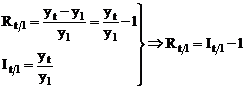
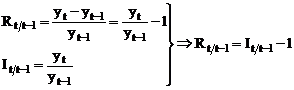
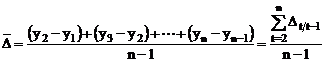
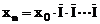
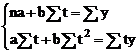
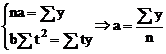 ;
;