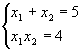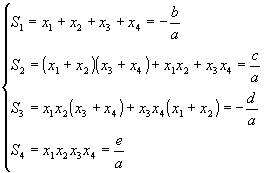Relatii intre radacini
si coeficienti (formulele lui Vičte)
Formulele lui Vičte
Fie  un polinom de grad n . Daca
un polinom de grad n . Daca 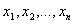 sunt radacinile lui f , atunci:
sunt radacinile lui f , atunci:

Invers, daca numerele complexe 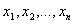 satisfac relatiile de mai sus, atunci ele
sunt radacinile polinomului f .
satisfac relatiile de mai sus, atunci ele
sunt radacinile polinomului f .
Observatie
Pentru polinomul de gradul III, 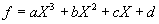 , cu
radacinile
, cu
radacinile 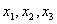 , relatiile
lui Vičte sunt:
, relatiile
lui Vičte sunt:
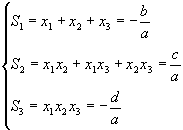 .
.
Exemplu
Sa se determine
radacinile polinomului 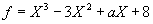 ,
, 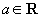 , stiind
ca produsul a doua radacini este egal cu 4. Aflati in
aceste conditii si parametrul a .
, stiind
ca produsul a doua radacini este egal cu 4. Aflati in
aceste conditii si parametrul a .
Rezolvare:
Relatiile lui Vičte in acest
caz sunt:
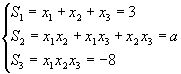 ; stiind
ca
; stiind
ca 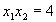 . Atunci din
. Atunci din 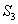 vom avea ca
vom avea ca 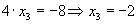 . Cum - 2 este
radacina a lui f rezulta ca f(-2) = 0
adica
. Cum - 2 este
radacina a lui f rezulta ca f(-2) = 0
adica 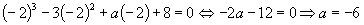 .
.
Pentru a afla celelalte doua radacini avem doua
metode:
Metoda I. (relatiile lui Vičte)
Inlocuim 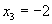 in prima relatie, vom avea sistemul
in prima relatie, vom avea sistemul 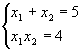 ale carui solutii vor fi
ale carui solutii vor fi 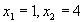
Metoda II. (Horner)
Cum - 2 este radacina a lui f rezulta ca (X
+ 2) divide pe f . Cu schema lui Horner aflam catul
impartirii lui f la (X + 2) si polinomul se va
scrie descompus f = 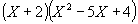 Rezolvand ecuatia
Rezolvand ecuatia 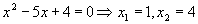 .
.
Observatie
Pentru polinomul de gradul IV, 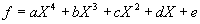
, este util sa cunoastem urmatoarea scriere
pentru relatiile lui Vičte:
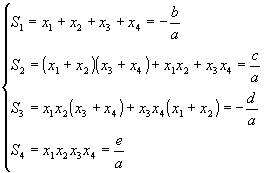



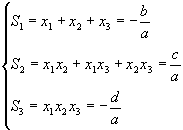 .
.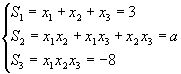 ; stiind
ca
; stiind
ca