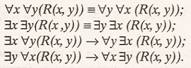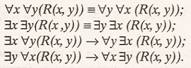Valoarea de adevar a formulelor
predicative inchise. Operatii cu formule predicative. Relatii intre
cuantori
Ca si in cazul formulelor logicii
propozitionale, rezolvarea problemei valorii de adevar a unei formule
predicative presupune interpretarea acesteia. A interpreta o formula
predicativa inseamna a-i asocia o clasa de obiecte numita univers de discurs U, care reprezinta sfera unei notuni-gen pentru termenii
aflati in componenta fomiulelor predicative. Fie, de pilda, Px
(x este profesor si U −
clasa persoanelor cu studii superioare sau medii speciale). In acest caz,
formula xPx ("orice persoana cu studii superioare sau medii speciale (x)
este profesor") este falsa, in timp ce formula xPx ("exista persoane cu studii superioare
sau medii speciale (x) profesori") este adevärata. In general,
adevarul sau falsitatea unei scheme (formule) predicative este
determinat(a) de urmatoarele conditii:
. o schema inchisa
(cuantificata) (propozitie simpla, atomara, de tipul xPx) este adevarata universal pentru
un univers (U) nevid, numai
daca toate obiectele din universul U
au proprietatea P, si este falsa numai daca in U exista cel putin un obiect
care nu are proprietatea P;
. o schema inchisa
(cuantificata) (de tipul xPx.) este adevarata existential pentru
un U nevid, numai daca in U exista cel putin un obiect
care are proprietatea P, si este falsa numai daca niciun obiect
din U nu are proprietatea P.
La schemele de functii si de
propozitii pot fi aplicati operatorii propozitionali. Daca
predicatul P este determinat in universul U,
atunci si negatia accstuia, adica predicatul ¬P, de asemenea
este determinat in U (vezi figura
5.1).
Formula ¬Px este adevarata numai
pentru acei x din U pentru care Px
este falsa. Deci, predicatele P si ¬P sunt complementare,
alcatuind doua clase (multimi) contradictorii care
epuizcaza universul U.

Daca universului U ii corespund predicatele P si Q, atunci acestui univers ii
vor corespunde si predicatele compuse:
1 Px Qx; 4.
Px → Qx;
2. Px Qx; 5. Px
← Qx;
3. Px w Qx; 6. Px ↔ Qx.
1. Formula prcdicativa Px) Q(x) este adevarata numai pentru
acei x din U pentru care ambele
predicate Px si Qx sunt adevarate. Cu alte cuvinte, acest predicat
compus este adevarat numai pentru acei x care reprezinta
intersectia valorilor de adevar ale predicatelor Px si Qx
(figura 5.2).
2. Formula predicativa Px Qx este adevarata numai pentru acei
x din U pentru care cel putin
unul din predicatele Px si Qx este adevarat. Cu alte cuvinte, acest
predicat compus este adevarat pentru acei x din U care alcatuiesc reuniunea
valorilor de adevar ale lui Px si Qx (figura 5.3).
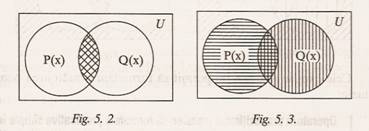
3. Formula predicativa Px w Qx este adevarata numai pentru acei
x din U pentru care Px)este
adevarat iar Qx este fals, sau Px este fals iar Qx adevarat (fig.
5.4):
(Px w Qx) ≡ (Px ¬Qx) (¬Px Qx)].
4. Formula predicativa Px→Qx este adevarata
numai pentru acei x din U pentru
care cel putin unul dintre predicatele ¬Px si Qx este adevarat
(reuniunea valorilor de adevar ale lui Px si Qx), deoarece (Px→Qx)
≡ (¬Px Qx) (fig.
5.5).
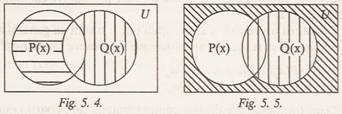
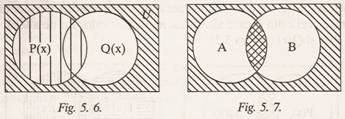
5. Formula predicativä Px←Qx este
adevarata numai pentru acei x din U care alcatuiesc reuniunea valorilor de adevar ale lui
Px si Qx, deoarece (Px←Qx) ≡ (¬Px Qx) (fig. 5.6).
6. In fine, formula predicativp Px↔Qx
este adevarata numai pentru acei x din U pentru care este adevarata cel putin una din formulele
Px Qx si ¬Px ¬Qx, deoarece
(Px↔Qx) ≡ (Px Qx) (¬Px ¬Qx) (fig.
5.7).
Cele expuse mai sus ne permit sa
formulam urmatoarea concluzie:
Operatorii propozitionali transforma
formulele predicative simple in formule predica-tive compuse si, prin
aceasta, logica propozitionala isi largeste
considerabil sfera de aplica-bilitate in procesul formalizarii
judecatilor naturale.
Daca in formula predicativa P(x1,
x2,. . . , xn), in care P este constanta
predicativa, iar x1, x2, , xn −
variabile individuale, vom inlocui variabilele individuale cu constante
individuale, vom obtine o propozitie atomara P(a1, a2,
,an) adevarata sau falsa. Atunci cand fiecare
element al universului U poseda
insusirea P, obtinem formule cuantificate de tipul xPx. Daca doar unele elemente ale acestui
univers poseda insusirea P, obtinem formule predicative
cuantificate de tipul xPx.
Cuantorii universali si existentiali
pot fi tratati ca generalizari ale conjunctiei si, respectiv,
ale disjunctiei neexclusive (inclusive):

Daca formulele predicative contin
variabile care apartin multimilor infinite,
acesti cuantori exprima conjunctii si disjunctii
infinite.
Pentru a transforma un predicat poliadic
intr-o propozitie, trebuie cuantificata fiecare variabilp
individuala. Cuantificand o formula predicativa diadica, de
tipul R(x, y), obtinem 8 combinatii:

Enunturile 1) si 2), de asemenea 3) si
4), au acelasi sens logic si, deci, aceeasi valoare de adevar.
Daca este adevarat 6), atunci este adevarat si 5) (dar nu
si myers). Daca este adevarat 8), atunci este adevarat
si 7) (dar nu si inivers).
Prin urmare, cuantorii omogeni (de acelasi
fel) sunt comutativi, iar cuantorii eterogeni sunt necomutativi: