Sectru si multimea caracteristica
In acest
paragraf si in urmatorul vom
studia comportarea ecuatiei

sau ceea ce este acelasi lucru, a
ecuatiei

In functie de parametrul complex 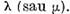 Aici si in
cele ce urmeaza U este presupus a fi un operator liniar continuu in
spatiul Banach complex X.
Aici si in
cele ce urmeaza U este presupus a fi un operator liniar continuu in
spatiul Banach complex X.
Consideram ambele ecuatii 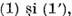 avand in vedere faptul ca ecuatia
(1) se considera de obicei in teoria ecuatiilor integrale , iar ecuatia
avand in vedere faptul ca ecuatia
(1) se considera de obicei in teoria ecuatiilor integrale , iar ecuatia 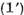 se considera de obicei in analiza
functionala abstracta la studiul proprietatilor
spectrale ale operatorului U .
se considera de obicei in analiza
functionala abstracta la studiul proprietatilor
spectrale ale operatorului U .
In functie de rezolubilitatea ecuatiei
(1) planul complex se imparte in doua multimi : multimea 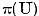 a valorilor lui
a valorilor lui 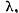 pentru care ecuatia (1) are o
solutie unica oricare ar fi membrul drept al ecuatiei ,
pentru care ecuatia (1) are o
solutie unica oricare ar fi membrul drept al ecuatiei , 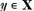 (prin urmare, operatorul
(prin urmare, operatorul 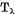 are invers continuu si multimea
are invers continuu si multimea 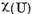 compusa din celelalte valori ale lui
compusa din celelalte valori ale lui 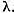 Punctele multimii
Punctele multimii 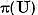 se numesc valori
nesingulare ale operatorului U, multimea
se numesc valori
nesingulare ale operatorului U, multimea 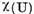 se numeste multime
caracteristica a operatorului U.
se numeste multime
caracteristica a operatorului U.
In mod analog vom introduce multimea 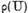 a acelor
a acelor 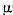 pentru care ecuatia
pentru care ecuatia 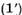 are o solutie unica , pentru orice
membru drept si multimea complementara
are o solutie unica , pentru orice
membru drept si multimea complementara 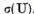
Punctele multimii 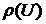 se numesc valori regulate ale operatorului U iar
insasi multimea
se numesc valori regulate ale operatorului U iar
insasi multimea 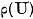 se numeste multime rezolventa a operatorului U; Multimea
se numeste multime rezolventa a operatorului U; Multimea 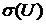 se numeste spectrul operatorului U.
se numeste spectrul operatorului U.
Daca pentru o valoare a lui 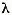 ecuatia
omogena
ecuatia
omogena
 (2)
(2)
are solutii diferite de zero atunci 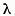 se numeste
valoarea caracteristica a operatorului U. Evident multimea
se numeste
valoarea caracteristica a operatorului U. Evident multimea 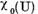 a tuturor
valorilor caracteristice este continuta in multimea
a tuturor
valorilor caracteristice este continuta in multimea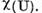 Fiecare
solutie a ecuatiei (2)se numeste element(vector) propriu corespunzator valorii caracteristice
date. Multimea
Fiecare
solutie a ecuatiei (2)se numeste element(vector) propriu corespunzator valorii caracteristice
date. Multimea
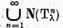
se numeste subspatiul radacina
iar dimensiunea lui (finita sau infinita ) se numeste multiplicitatea valorii caracteristice 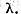 Numarul r
de multimi distincte din sirul
Numarul r
de multimi distincte din sirul
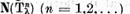 se numeste rangul valorii caracteristice
se numeste rangul valorii caracteristice
Daca in locul
ecuatiei (2) consideram o ecuatie omogena
corespunzatoare ecuatiei 
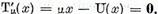
atunci ajungem la notiunea de valoare proprie
(sau numar propriu) de element (sau vector) propriu si de
subspatiu radacina corespunzator valorii proprii date Sa
observam ca daca U este operator autoadjunct intr-un spatiu
Hilbert si 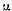 este o valoare proprie a sa atunci rangul ei r
=1 adica
este o valoare proprie a sa atunci rangul ei r
=1 adica
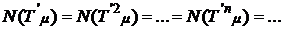 (3)
(3)
si de aceea in acest caz subspatial radacina este  adica se
compune din toti vectorii proprii ai operatorului U
adica se
compune din toti vectorii proprii ai operatorului U
Sa demonstram relatia (3). Deoarece valorile proprii ale
unui operator autoadjunct sunt reale operatorul 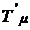 si toate
puterile sale sunt operatori autoadjuncti. Omitand pentru simplitate
indicele
si toate
puterile sale sunt operatori autoadjuncti. Omitand pentru simplitate
indicele 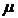 si alegand
si alegand 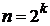 vom avea pentru
vom avea pentru 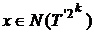
(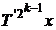 ,
,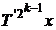 ) = (
) = (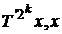 ) = 0,
) = 0,
de unde
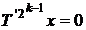
Continuand astfel ajungem la egalitatea 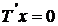 adica
adica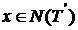 si deci
si deci 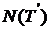
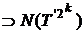 Incluziunea opusa are loc pentru un
operator arbitrar. Astfel,
Incluziunea opusa are loc pentru un
operator arbitrar. Astfel, 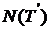
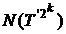 (k=1,2, . ).Daca
se considera mai departe un
(k=1,2, . ).Daca
se considera mai departe un
n =2,3, arbitrar, atunci alegand k astfel
incat 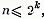 vom avea incluziunile evidente
vom avea incluziunile evidente 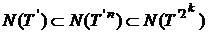 De aici,
De aici, 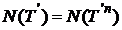
Vom mentiona acum o legatura
simpla intre spectrul si multimea caracteristica a unuia
si aceluiasi operator U. Este
usor de vazut ca daca 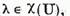 atunci
atunci
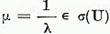
si invers. Evident in acelasi mod sunt
legate si valorile caracteristice cu valorile proprii ale operatorului U.
Aici este important sa avem invedere ca elementul propriu
corespunzator valorii caracteristice 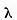 va fi totodata elementul propriu
corespunzator valorii proprii
va fi totodata elementul propriu
corespunzator valorii proprii 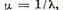 si reciproc . Mai departe deoarece pentru
si reciproc . Mai departe deoarece pentru
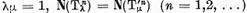 observatia anterioara se extinde
si la subspatiile proprii. Din aceasta cauza nu este
necesar sa distingem notiunile de vector propriu corespunzator
unei valori caracteristice si de vector propriu corespunzator unei valori proprii fapt care se
reflecta si in terminologia introdusa mai sus.
observatia anterioara se extinde
si la subspatiile proprii. Din aceasta cauza nu este
necesar sa distingem notiunile de vector propriu corespunzator
unei valori caracteristice si de vector propriu corespunzator unei valori proprii fapt care se
reflecta si in terminologia introdusa mai sus.
Legatura
indicata intre multimea caracteristica si spectru permite
sa se considere , dupa cum este comod, doar una dintre aceste
doua notiuni paralele si , in esenta, echivalente dand
ambele formulari numai in cazuri exceptionale
Vom enunta acum cateva propozitii simple
legate de notiunile introduse mai sus.
Relatia 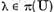 este echivalenta cu existenta inversului
bilateral continuu
este echivalenta cu existenta inversului
bilateral continuu 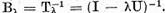
Multimea valorilor nesingulare este
deschisa si prin urmare multimea caracteristica este
inchisa.
Aceasta rezulta din teorema care afirma
ca daca un operator are invers continuu, atunci si un operator
suficient de apropiat in norma de aceasta are invers continuu In cazul nostru
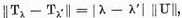
astfel incat daca exista 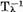 atunci pentru diferenta
atunci pentru diferenta 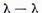 suficient de mica, va exista si
suficient de mica, va exista si 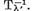
Discul
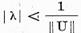
este
continut in multimea 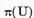 ; prin urmare
spectrul
; prin urmare
spectrul 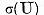 este in intregime continut in discul
este in intregime continut in discul 
Pentru a stabili valabilitatea acestei
afirmatii este suficient sa aplicam teorema lui Banach privind
operatorul invers. Multimile 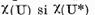 sunt dispuse simetric fata de axa
reala.
sunt dispuse simetric fata de axa
reala.
Intradevar
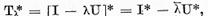
deci operatorii 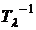 si
si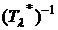 exista in
acelasi timp.
exista in
acelasi timp.
Daca X este spatiu cu
structura reala , Iar U operator real, atunci multimea 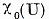 este simetrica fata de axa
reala. In afara de aceasta daca
este simetrica fata de axa
reala. In afara de aceasta daca 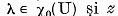 este un vector propriu corespunzator ,
atunci valorii caracteristice
este un vector propriu corespunzator ,
atunci valorii caracteristice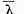 ii va corespunde
vectorul propriu
ii va corespunde
vectorul propriu 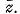
Intradevar

de unde rezulta ca
egalitatatile 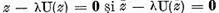 sunt echivalente.
sunt echivalente.

