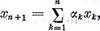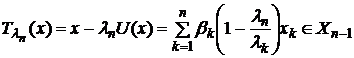Structura multimii caracteristice pentru operator compact

Structura multimii caracteristice pentru operator compact

In cazul in care U este operator compact structura multimii caracteristice poate fi descrisa suficient de complet.

Teorema III.2.1. Daca U este un operator compact atunci

a) multimea caracteristica este formata numai din valori caracteristice adica 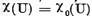; pe langa aceasta fiecare valoare caracteristica are multiplicitate finita

b) pentru orice   discul 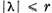contine doar un numar finit de valori caracteristice.

c) daca si daca 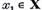este un element propriu corespunzator lui 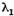iar 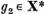este un element propriu corespunzator lui 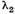atunci

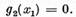
Demonstratie. a) Conform teoremei I.4.1 daca 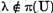atunci ecuatia omogena (2) are o solutie nenula. Faptul ca subspatiul propriu este finit-dimensional rezulta din lema I.1.2. Intradevar conform acestei leme, exista un astfel incat 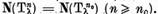De aceea in acest caz, subspatiul propriu este 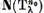. Dar

unde 

este evident operator compact. De aceea pe baza teoremei deja mentionate I.4.1. multimea solutiilor ecuatiilor omogene

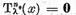
formeaza un subspatiu finit-dimensional, iar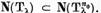

b) Sa presupunem contrariul anume ca intr-un disc 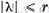este continuta o multime infinita de valori caracteristice. Sa alegem din aceasta multime un sir 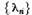de valori caracteristice distincte 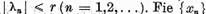un sir de vectori proprii nenuli corespunzatori

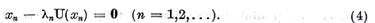
Vom arata (prin inductie)ca pentru orice n = 1,2, . . elementele sunt liniar independente.Pentru n =1 aceasta este adevarata. Sa presupunem ca propozitia este adevarata pentru 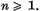. O vom verifica atunci pentru elementele . Presupunand contrariul vom avea

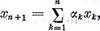
de unde in virtutea relatiei (4)

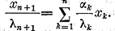
Introducand aceasta expresie in egalitate precedenta vom gasi

Deoarece

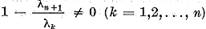
obtinem astfel ca elementele 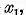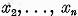sunt liniar dependente,contrar ipotezei inductiei.

Sa formam multimile 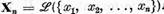. Deoarece conform celor demonstrate 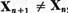putem gasi pe baza lemei cvasiperpendicularei elementele 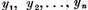astfel incat

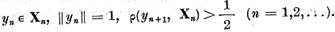   (5)

Daca 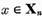adica daca

atunci

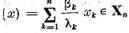
Totodata

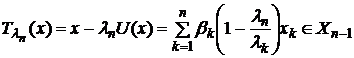
Fie . Sa consideram expresia

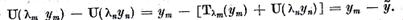
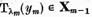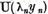conform celor demonstrate si є 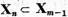. Prin urmare

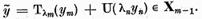
Ca urmare a relatiilor (5)

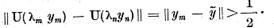
dar aceasta contrazice compacitatea operatorului U intrucat sirul 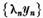este marginit

c) Avem 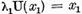si 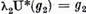. Prin urmare

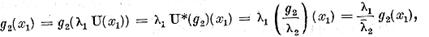
ceea ce este posibil, in virtutea faptului ca 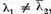numai daca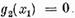

In incheiere sa remarcam ca daca U este operator compact intr-un spatiu infinit-dimensional X atunci punctul zero apartine spectrului operatorului U